密码学总结（二）一、非对称加密二、单向散列函数三、消息认证码

80 阅读 0 评论 53 点赞

我是靠谱客的博主执着帆布鞋，最近开发中收集的这篇文章主要介绍密码学总结（二）一、非对称加密二、单向散列函数三、消息认证码，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

一、非对称加密

在对称密码中，由于加密和解密都需要使用相同秘钥。假如向接收者配送密钥过程中发生秘钥泄露，就可能导致泄的情况出现。而非对称加密的出现可以很好解决该问题。

非对称加密的密钥分为加密密钥和解密密钥两种。发送者用加密密钥对消息进行加密，接收者用解密密钥对密文进行解密。解密密钥从一开始就是由接收者自己保管的，这样就解决了上面秘钥配送过程中可能遇到的泄密问题。
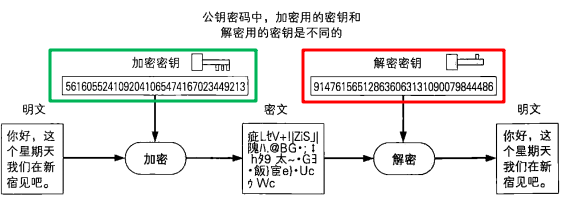
在这里插入图片描述
非对称加密中，加密密钥一般是公开的，任意用户都可以获得。正是由于加密密钥是公开的，因此加密秘钥也被称为公钥（PublicKey）。相对地，解密秘钥是绝对不能够公开的，由用户自己负责保管，因此称为私钥（PrivateKey）。公钥和私钥统称为密钥对（keypair）。

1.1 非对称加密通讯流程

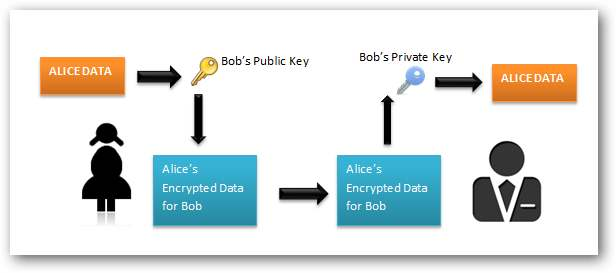
在这里插入图片描述
假设Alice要给Bob发送一条消息。由于消息的重要性，需要对消息进行加密处理。在非对称加密通讯中，通讯过程是由消息接收方Bob负责发起的。

Bob生成一个包含公钥和私钥的秘钥对；
Bob将公钥发送给Alice，私钥自己保管；
Alice接收到Bob发送过来的公钥后，使用该公钥对发送消息进行加密处理后，再把加密数据发送给Bob；
Bob接收到Alice发送过来的加密数据后，使用私钥进行解密，得到原文；

如果在通讯过程中Tracker窃取了数据，但是只要Bob的秘钥数据没有泄漏， Tracker就无法完成解密操作，数据还是安全的。

下面介绍两种常见的非对称加密算法：RSA和椭圆曲线。

1.2 RSA

RSA加密算法是一种非对称加密算法，在公开密钥加密和电子商业中RSA被广泛使用。RSA是1977年由RonRivest、AdiShamir和LeonardAdleman 一起提出的。RSA就是它们三人的首字母所组成的。

1.2.1 RSA加密原理

RSA的加密过程可以用以下公式来表达：

$密文=明文 ^ E mod N（RSA加密）$
也就是说，RSA的密文是对代表明文的数字执行E次方运算后，将运算结果对N取模得到的，这个余数就是密文。因此，E和N就是RSA加密的密钥，E和N的组合就是公钥。一般把公钥简写成 “(E，N)” 或者 “{E, N}"的形式。

简单来说，只要知道E和N就可以完成加密运算。但是，E和N并不是随便什么数都可以的，它们必须经过严密的计算得到的。

1.2.2 RSA解密原理

RSA的解密过程可以用以下公式来表达：
$明文=密文^DmodN（RSA解密）$
也就是说，对代表密文数字执行D次方运算后，将运算结果对N取模，这个余数就是明文。因此，D和N就是RSA解密的密钥，D和N的组合就是私钥。只有知道D和N两个数的人才能够完成解密的运算。

值得注意的是，解密公式的数字N和加密公式的数字N是相同的。

简单来说，只要知道D和N就可以完成解密运算。当然，D也并不是随便什么数都可以的，作为解密密钥的D，和数字E有着相当紧密的联系。

1.2.3 如何生成秘钥对

生成私钥的操作步骤：

第一步：使用rsa中的GenerateKey方法，该方法使用随机数据生成器random生成一对具有指定字位数的RSA密钥；

func GenerateKey(random io.Reader, bits int) (priv *PrivateKey, err error)

第二步：通过x509标准将得到的ras私钥序列化为ASN.1的DER编码字符串；

func MarshalPKCS1PrivateKey(key *rsa.PrivateKey) []byte

第三步：将私钥字符串设置到pem格式块中；

type Block struct {
    Type    string            // 类型，私钥为"RSA PRIVATE KEY"，公钥为“RSA PUBLIC KEY”
    Headers map[string]string // 可选的头信息
    Bytes   []byte            // 解码后的数据
}

第四步：通过pem将设置好的数据进行编码, 并写入磁盘文件中；

func Encode(out io.Writer, b *Block) error

生成公钥的操作步骤：

第一步：从得到的私钥对象中将公钥信息取出；

publicKey := privateKey.PublicKey // privateKey为私钥对象

第二步：通过x509标准将得到的rsa公钥序列化为字符串；

func MarshalPKIXPublicKey(pub interface{}) ([]byte, error)

第三步：将公钥字符串设置到pem格式块中；
第四步：通过pem将设置好的数据进行编码, 并写入磁盘文件；

代码实现：

func generateKey() {
	//============== 生成私钥 =============
	// 使用rsa中的GenerateKey方法生成私钥
	privateKey, err := rsa.GenerateKey(rand.Reader, 1024)
	if err != nil {
		panic(err)
	}
	// 通过x509标准将得到的ras私钥序列化为ASN.1 的 DER编码字符串
	derText := x509.MarshalPKCS1PrivateKey(privateKey)
	// 将私钥字符串设置到pem格式块中
	block := pem.Block{
		Type: "rsa private key",
		Bytes: derText,
	}
	// 创建文件，用于保存私钥数据
	file, err := os.Create("private.pem")
	if err != nil {
		panic(err)
	}
	// 释放资源
	defer file.Close()
	// 通过pem将设置好的数据进行编码, 并写入磁盘文件中
	pem.Encode(file, &block)

	//============== 生成公钥 =============
	// 从得到的私钥对象中将公钥信息取出
	publicKey := privateKey.PublicKey
	// 通过x509标准将得到 的rsa公钥序列化为字符串
	derText, err = x509.MarshalPKIXPublicKey(&publicKey)
	if err != nil {
		panic(err)
	}
	// 将公钥字符串设置到pem格式块中
	block = pem.Block {
		Type: "rsa public key",
		Bytes: derText,
	}
	// 创建文件，用于存储公钥数据
	file, err = os.Create("public.pem")
	if err != nil {
		panic(err)
	}
	// 释放资源
	defer file.Close()
	// 通过pem将设置好的数据进行编码, 并写入磁盘文件
	pem.Encode(file, &block)
}

1.2.4 如何使用RSA

使用公钥加密的操作步骤：

第一步：将公钥文件中的公钥读出, 得到使用pem编码的字符串；
第二步：将得到的字符串进行解码操作；
第三步：使用x509将编码之后的公钥解析出来；
第四步：使用得到的公钥通过rsa进行数据加密；

使用私钥解密的操作步骤：

第一步：将私钥文件中的私钥读出, 得到使用pem编码的字符串；
第二步：将得到的字符串进行解码操作；
第三步：使用x509将编码之后的私钥解析出来；
第四步：使用得到的私钥通过rsa进行数据解密；

代码实现：

// rsa加密
func RsaEncrypt(publicKeyFile string, plainText string) []byte {
	// 将公钥文件中的公钥读出, 得到使用pem编码的字符串
	file, err := os.Open(publicKeyFile)
	if err != nil {
		panic(err)
	}
	defer file.Close()
	fileInfo, err := file.Stat()
	if err != nil {
		panic(err)
	}
	buf := make([]byte, fileInfo.Size())
	file.Read(buf)
	// 使用pem.Decode将得到的字符串解码
	block, _ := pem.Decode(buf)
	// 使用x509将解码后的公钥解析出来
	pubInterface, err := x509.ParsePKIXPublicKey(block.Bytes)
	if err != nil {
		panic(err)
	}
	publicKey, ok := pubInterface.(*rsa.PublicKey)
	if !ok {
		panic("publicKey is not rsa.PublicKey.")
	}
	// 使用公钥进行数据加密
	cipherText, err := rsa.EncryptPKCS1v15(rand.Reader, publicKey, []byte(plainText))
	if err != nil {
		panic(err)
	}
	return cipherText
}

// rsa解密
func RsaDecrypt(privateKeyFile string, cypherText []byte) []byte {
	// 将私钥文件中的私钥读出, 得到使用pem编码的字符串
	file, err := os.Open(privateKeyFile)
	if err != nil {
		panic(err)
	}
	defer file.Close()
	fileInfo, err := file.Stat()
	if err != nil {
		panic(err)
	}
	buf := make([]byte, fileInfo.Size())
	file.Read(buf)
	// 使用pem将得到的字符串解码
	block, _ := pem.Decode(buf)
	// 使用x509将解码后的私钥解析出来
	privateKey, err := x509.ParsePKCS1PrivateKey(block.Bytes)
	if err != nil {
		panic(err)
	}
	// 使用私钥进行数据解密
	plainText, err := rsa.DecryptPKCS1v15(rand.Reader, privateKey, cypherText)
	if err != nil {
		panic(err)
	}
	return plainText
}

// 测试
func main() {
	generateKey()
	cypherText := RsaEncrypt("public.pem", "hello rsa")
	fmt.Println("加密后的字符串：", cypherText)
	plainText := RsaDecrypt("private.pem", cypherText)
	fmt.Println("解密后的字符串：", string(plainText))
}

1.3 ECC椭圆曲线

椭圆曲线（英语：Elliptic curve cryptography，缩写为 ECC）在密码学中的使用是在1985年由Neal Koblitz和Victor Miller分别独立提出的。ECC的主要优势是在某些情况下，它比其他加密算法使用更小的密钥，提供更高的安全级别。ECC 164位的密钥相当于RSA 1024位密钥提供的保密强度，而且计算量更少，处理速度更快。目前我国居民二代身份证正在使用 256 位的椭圆曲线密码，虚拟货币比特币也选择ECC作为加密算法。

1.4 对称加密和非对称加密的疑惑

问题1：非对称加密比对称加密的机密性更高吗？

这个问题无法回答, 以为机密性高低是根据秘钥长度而变化的。

问题2：采用1024bit 秘钥长度的非对称加密, 和采用128bit秘钥长度的对称加密中, 是秘钥更长的非对称加密更安全吗?

不是。从下表看出，1024比特的公钥密码与128比特的对称密码相比，反而是128比特对称密码的抵御暴力破解的能力更强。

对称加密的秘钥长度	非对称加密的秘钥长度
128比特	2304比特
112比特	1792比特
80比特	768比特
64比特	512比特
56比特	384比特

问题3：有了非对称加密，以后对称加密会被替代吗？

不会，一般来说，在采用具备同等机密性的密钥长度的情况下，非对称加密的处理速度只有对称加密的几百分之一。因此，非对称加密并不适合用来对很长的消息内容进行加密。根据目的的不同，还可能会配合使用对称加密和非对称加密，例如，混合密码系统就是将这两种密码组合而成的。

二、单向散列函数

2.1 什么是单项散列函数

单向散列函数（One-way hash function），又称单向Hash函数或杂凑函数。单向散列函数就是把任意长的输入消息串变化成固定长的输出串且由输出串难以得到输入串的一种函数。这个输出串称为该消息的散列值。一般用于产生消息摘要，密钥加密等。
在这里插入图片描述
这里的消息不一定是文字，也可以是图像、声音等文件。无论任何消息，单向散列函数都会将它作为单纯的比特序列来处理，计算出散列值。散列值的长度和消息的长度无关。无论消息是1比特，还是1Mb，甚至是I00Mb，单向散列函数都会计算出固定长度的散列值。

2.2 单向散列函数的特性

散列值的长度是固定的
能够快速计算出散列值
具有单向性
消息不同散列值也不同

两个不同的消息产生同一个散列值的情况称为碰撞（collision）。如果使用单向散列函数进行数据完整性的检查，则需要确保不可能被人为地发现碰撞。

2.3 单向散列函数应用

2.3.1 检测软件是否被篡改

很多软件，尤其是安全相关的软件都会把通过单向散列函数计算出的散列值公布在自己的官方网站上。用户在下载到软件之后，可以自行计算散列值，然后与官方网站上公布的散列值进行对比。通过散列值，用户可以确认自己所下载到的文件与软件作者所提供的文件是否一致。

这样的方法，在可以通过多种途径得到软件的情况下非常有用。为了减轻服务器的压力，很多软件作者都会借助多个网站（镜像站点）来发布软件，在这种情况下，单向散列函数就会在检测软件是否被篡改方面发挥重要作用。

2.3.2 消息认证码

消息认证码是将“发送者和接收者之间的共享密钥”和“消息，进行混合后计算出的散列值。使用消息认证码可以检测并防止通信过程中的错误、篡改以及伪装。

2.3.3 数字签名

数字签名是现实社会中的签名（sign）和盖章这样的行为在数字世界中的实现。数字签名的处理过程非常耗时，因此一般不会对整个消息内容直接施加数字签名，而是先通过单向散列函数计算出消息的散列值，然后再对这个散列值施加数字签名。

2.3.4 伪随机生成器

密码技术中所使用的随机数需要具备“事实上不可能根据过去的随机数列预测未来的随机数列”这样的性质。为了保证不可预测性，可以利用单向散列函数的单向性。

2.3.5 一次性口令

一次性口令经常被用于服务器对客户端的合法性认证。在这种方式中，通过使用单向散列函数可以保证口令只在通信链路上传送一次。因此，即使窃听者窃取了口令，也无法使用。

2.4 常见的单向散列函数

2.4.1 MD5

MD5是由Rwest于1991年设计的单项散列函数，全称是Message Digest Algorithm 5，译为“消息摘要算法第5版”。

MD5的特点：
1）对输入信息生成唯一的128比特的散列值；
2）明文不同，则散列值一定不同，明文相同，则散列值一定相同；
3）根据输出值，不能得到原始的明文，即其过程不可逆；

MD5的强抗碰撞性已经被攻破，也就是说，现在已经能够产生具备相同散列值的两条不同的消息，因此它也已经不安全了。

示例代码：

// 方式一
func GetMD5(plainText []byte) string {
	// 1. 创建一个使用MD5校验的Hash对象`
	myHash := md5.New()
	// 2. 通过io操作将数据写入hash对象中
	myHash.Write(plainText )
	// 3. 计算结果
	result := myHash.Sum(nil)
	fmt.Println(result)
	// 4. 将结果转换为16进制格式字符串
	res := hex.EncodeToString(result)
	return res
}

// 方式二
func GetMD5(plainText []byte) string {
	// 执行md5加密
	result := md5.Sum(plainText)
	// 数据格式化为16进制格式字符串
	res := hex.EncodeToString(result[:])
	return  res
}

2.4.2 SHA-1、SHA-256、SHA-384、SHA-512

SHA-1是由NIST（NationalInstituteOfStandardsandTechnology，美国国家标准技术研究所）设计的一种能够产生160比特散列值的单向散列函数。SHA-1的消息长度存在上限，但这个值接近于2⁶⁴比特，是个非常巨大的数值，因此在实际应用中没有问题。

SHA-256、SHA-384和SHA-512都是由NIST设计的单向散列函数，它们的散列值长度分别为256比特、384比特和512比特。这些单向散列函数合起来统称SHA-2，它们的消息长度也存在上限（SHA-256的上限接近于 2⁶⁴ 比特，SHA-384 和 SHA-512的上限接近于 2¹²⁸ 比特）。SHA-1的强抗碰撞性已于2005年被攻破, 也就是说，现在已经能够产生具备相同散列值的两条不同的消息。不过，SHA-2还尚未被攻破。

示例代码：

// 方式一
func GetSha() string {
	// 1.创建哈希接口对象
	myHash := sha256.New()
	// 2.添加数据
	myHash.Write([]byte("hello "))
	myHash.Write([]byte("world "))
	// 3.计算结果
	result := myHash.Sum(nil)
	// 4.格式化为16进制
	res := hex.EncodeToString(result)
	return res
}

// 方式二
func GetSha2() string {
	// 直接调用Sum256方法生成散列值
	result := sha256.Sum256([]byte("hello world "))
	res := hex.EncodeToString(result[0:len(result)])
	return res
}

三、消息认证码

3.1 什么是消息认证码

消息认证码（Message Authentication Code）是一种确认完整性并进行认证的技术，取三个单词的首字母，简称为MAC。

消息认证码的输入包括任意长度的消息和一个发送者与接收者之间共享的密钥，它可以输出固定长度的数据，这个数据称为MAC值。根据任意长度的消息输出固定长度的数据，这一点和单向散列函数很类似。但是单向散列函数中计算散列值时不需要密钥，而消息认证码中则需要使用发送者与接收者之间共享的密钥。
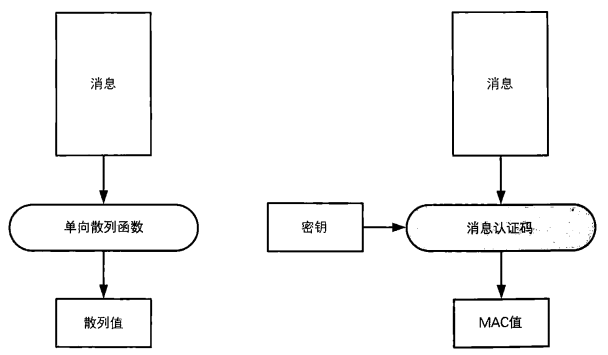
在这里插入图片描述
要计算MAC必须持有共享密钥，没有共享密钥的人就无法计算MAC值，消息认证码正是利用这一性质来完成认证的。此外，和单向散列函数的散列值一样，哪怕消息中发生1比特的变化，MAC值也会产生变化，消息认证码正是利用这一性质来确认完整性的。

3.2 消息认证码的使用步骤

下面以银行汇款为例，介绍消息认证码的使用过程。
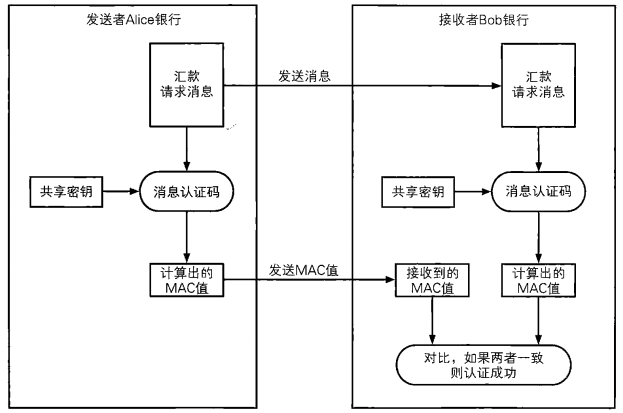
在这里插入图片描述

发送者Alice和接收者Bob事先共享秘钥；
Alice根据汇款请求消息使用共享秘钥计算出MAC值；
Alice将汇款请求消息与MAC值一起发送给Bob；
Bob根据接收到的汇款请求信息使用共享秘钥计算出MAC值；
Bob将自己计算的MAC值与Alice发送过来的MAC值进行比较，如果两个MAC值一致，则Bob就可以断定汇款请求消息是由Alice发送过来；如果不一致，则可以断定消息不是来自于Alice；

3.3 HMAC

HMAC是一种使用单向散列函数来构造消息认证码的方法（RFC2104规范），其中HMAC的H就是Hash的意思。HMAC中所使用的单向散列函数并不仅限于一种，任何高强度的单向散列函数都可以被用于HMAC,如果将来设计出新的单向散列函数，也同样可以使用。使用SHA-I、MD5、RIPEMD-160所构造的HMAC，分别称为HMAC-SHA-1、HMAC-MD5和HMAC-RlPEMD。

消息认证码的内部实现：

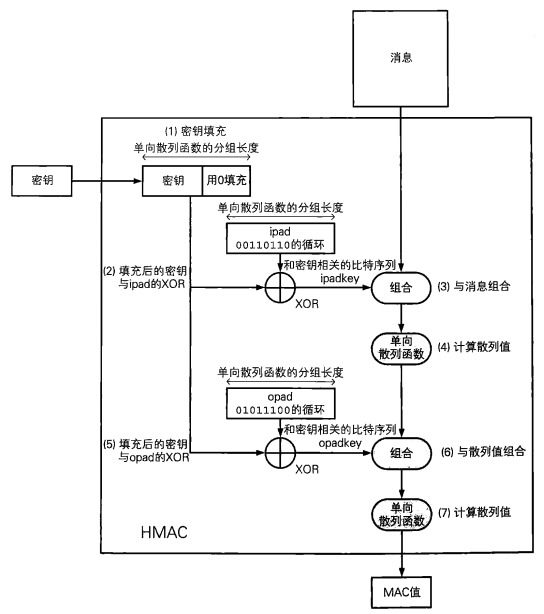
从上图可以看出，通过单向散列函数生成的MAC值，一定是一个与输入消息和密钥相关的长度固定的比特序列。
使用单向散列函数生成HMAC：

func GenerateHmac(plainText, key []byte) []byte {
	// 1.创建哈希接口，需要指定使用的哈希算法和密钥
	myHash := hmac.New(sha1.New, key)
	// 2.给哈希对象添加数据
	myHash.Write(plainText)
	// 3.计算散列值
	hashText := myHash.Sum(nil)
	return hashText
}

func VerifyHmac(plainText, key, hashText []byte) bool {
	// 1.创建哈希接口，需要指定使用的哈希算法和密钥
	myHash := hmac.New(sha1.New, key)
	// 2.给哈希对象添加数据
	myHash.Write(plainText)
	// 3.计算散列值
	hashText2 := myHash.Sum(nil)
	// 4.比较散列值是否相等
	return hmac.Equal(hashText, hashText2)
}

// 测试
func main() {
	plainText := []byte("hello world")    // 明文
	key := []byte("123456")         // 共享密钥
	hmac := GenerateHmac(plainText, key) // 生成消息认证码
	isEq := VerifyHmac(plainText, key, hmac)
	fmt.Printf("校验结果：%tn", isEq)
}

注意：使用消息认证码执行认证所使用的秘钥和哈希函数必须相同。

消息认证码的弊端：
1）无法通过第三方证明，不能让大家信服；
2）无法阻止对方反悔；

最后

以上就是执着帆布鞋为你收集整理的密码学总结（二）一、非对称加密二、单向散列函数三、消息认证码的全部内容，希望文章能够帮你解决密码学总结（二）一、非对称加密二、单向散列函数三、消息认证码所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。

本文分类：go
浏览次数：80 次浏览
发布日期：2023-09-07 00:40:28
本文链接：https://www.kaopuke.com/article/k-p-k_14_uzo_10_f3_14_z_22_x.html

密码学总结（二）一、非对称加密二、单向散列函数三、消息认证码

概述

一、非对称加密

1.1 非对称加密通讯流程

1.2 RSA

1.2.1 RSA加密原理

1.2.2 RSA解密原理

1.2.3 如何生成秘钥对

1.2.4 如何使用RSA

1.3 ECC椭圆曲线

1.4 对称加密和非对称加密的疑惑

二、单向散列函数

2.1 什么是单项散列函数

2.2 单向散列函数的特性

2.3 单向散列函数应用

2.3.1 检测软件是否被篡改

2.3.2 消息认证码

2.3.3 数字签名

2.3.4 伪随机生成器

2.3.5 一次性口令

2.4 常见的单向散列函数

2.4.1 MD5

2.4.2 SHA-1、SHA-256、SHA-384、SHA-512

三、消息认证码

3.1 什么是消息认证码

3.2 消息认证码的使用步骤

3.3 HMAC

最后

评论列表共有 0 条评论

发表评论取消回复

密码学总结（二）一、非对称加密二、单向散列函数三、消息认证码

概述

一、非对称加密

1.1 非对称加密通讯流程

1.2 RSA

1.2.1 RSA加密原理

1.2.2 RSA解密原理

1.2.3 如何生成秘钥对

1.2.4 如何使用RSA

1.3 ECC椭圆曲线

1.4 对称加密和非对称加密的疑惑

二、单向散列函数

2.1 什么是单项散列函数

2.2 单向散列函数的特性

2.3 单向散列函数应用

2.3.1 检测软件是否被篡改

2.3.2 消息认证码

2.3.3 数字签名

2.3.4 伪随机生成器

2.3.5 一次性口令

2.4 常见的单向散列函数

2.4.1 MD5

2.4.2 SHA-1、SHA-256、SHA-384、SHA-512

三、消息认证码

3.1 什么是消息认证码

3.2 消息认证码的使用步骤

3.3 HMAC

最后

相关文章

评论列表共有 0 条评论

发表评论 取消回复

发表评论取消回复