1 基本形式

$f(\mathbf{x})=w_1{x}_1+w_2{x}_2+...+w_d{x}_d+b={\mathbf{w}}^T\mathbf{x}+b$
线性模式有很好的解释性，直观的表达了各个特征的重要性。

2 线性回归

通过最小化均方误差来求解参数$\mathbf{w}$和$b$。
对$y$变形可以求解非线性模型，如$lny={\mathbf{w}}^T\mathbf{x}+b$。

3 对数几率回归

对于分类问题，最好将输出$y$约束在0-1之间，可以使用sigmoid函数进行约束：$y=\frac{1}{1+e^{(}-{\mathbf{w}}^T\mathbf{x}+b)}$，此时可认为输出y是输入数据x为正例的概率。通过极大似然估计求解参数。

4 多分类学习

4.1 OvO和OvR

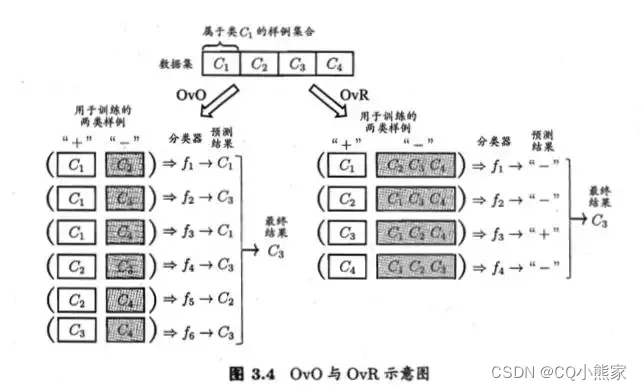
OvO即一对一。每次选择两类数据训练出一个分类器，对N个类别则可以训练出N(N-1)/2个分类器。N(N-1)/2个分类器对新数据进行分类会得到N(N-1)/2个结果，根据多数票决原则决定新数据的类别。
OvR即一对其余。每次选择一类数据作为正例，剩下的N-1类数据作为负例，训练出一个分类器。N个类别可以训练出N个分类器。N个分类器对新数据进行分类会得到N个结果，看哪一个分类器的分类结果为正。

4.2 MvM和ECOC

MvM是多对多。一种常用的MvM技术是纠错输出码ECOC。每次选择若干类数据作为正例，若干其他类作为反例，训练分类器并进行编码。以上图OvR为例，现在训练得到四个分类器，$C_3$类的编码为0010，新数据经过这四个分类器之后的编码若为0100，则是第二类；若为0010，则为第三类；若为0110，则检测出某个分类器是错的。

5 类别不平衡问题

类别不平衡问题指的是当样本中正例负例的数量相差较多时，分类器在训练时会更加看重数量多的那一类。这显然是不公平的，不能说因为他们人多就看重他们，我们人少就看轻我们，大家都是平等的。
当类别不平衡时，可以通过对数量多对类别欠采样，减少其数量；可以通过对数量少的类别进行过采样，增加其数量；还可以通过阈值转移，让训练好的不公平的分类器恢复公平。

6 参考文献

周志华 机器学习 清华大学出版社
谢文睿、秦州 机器学习公式详解 人民邮电出版社
部分图片源自网络，如有侵权联系删除

最后

以上就是腼腆手套最近收集整理的关于【读书笔记】周志华 机器学习 第三章 线性模型1 基本形式2 线性回归3 对数几率回归4 多分类学习5 类别不平衡问题6 参考文献的全部内容，更多相关【读书笔记】周志华内容请搜索靠谱客的其他文章。