4.选择两个UCI数据集,比较10折交叉验证法和留一法所估计出的对率回归的错误率。
选取了UCI上iris数据集,内部共150个数据,3种类别,每类50个样本。
每次选择两类做二分类计算,做3轮计算。每轮选取100个样本,10折法选45正45反,剩下10个作为验证,一共10组,共验证100例;留一法每次留1个做验证,一共100组,也是100例。每个方法最终验证300例,直接比较错误分类的个数就能评价两种方法在该数据集上的适用程度。
一:Excel表处理iris数据集
iris数据集
二:10折交差验证
%对率回归 iris数据集
%数据集3类数据 A-AX AY-CV CW-ET 各50组
%为了程序读取方便对数据集做了处理1-6 1,2类数据 7-12 1,3类数据 13-18 2,3类数据 A-CV
x = xlsread('E:Program Filesoctaveiris.xlsx', 'Sheet1', 'A52:E151'); %训练数据每次取两类100个
y = xlsread('E:Program Filesoctaveiris.xlsx', 'Sheet1', 'F52:F151');
%数据集分类用了1,2,3来表示 使用不同的类别对y的处理也不同(总之保证y的取值为{0,1})
y = y-1;
k=100;
%10折交差与留1法主体部分一样,只是在过滤用来验证样本的地方有区别 为了简单复制了大部分代码
%10折交差验证
err0=0;%记录错误分类的次数
for tn=0:9
old_l=0; %记录上次计算的l
b=[0;0;0;0;1]; %初始参数 (自定义)
while(1)
cur_l=0;
bx=zeros(k,1);
%计算当前参数下的l
for i=1:k
if fix(mod(i-1,50)/5) == tn %跳过用来检验的样本
continue;
end
bx(i) = b.'*(x(i,:))';
if bx(i)>30 %防止exp函数的参数过大导致无穷大 手动计算
tlog=bx(i);
else
tlog=log(1+exp(bx(i)));
end
cur_l = cur_l - y(i)*bx(i) +tlog;
end
%迭代终止条件
if abs(cur_l-old_l)<0.0001
break;
end
%更新参数(牛顿迭代法)以及保存当前l
old_l = cur_l;
p1=zeros(k,1);
dl=0;
d2l=0;
for i=1:k
if fix(mod(i-1,50)/5) == tn %跳过用来检验的样本
continue;
end
p1(i) = 1 - 1/(1+exp(bx(i)));
dl = dl - x(i,:)'*(y(i)-p1(i));
d2l = d2l + x(i,:)' * (x(i,:)').'*p1(i)*(1-p1(i));
end
b = b - d2ldl;
end
for i=0:1 %用来检验的样本 如果出错则计数+1 每组5个1类5个2类
for j=1:5
tmp = 1/(1+exp(-b.'*x(i*50+5*tn+j,:)'));
tmp = (tmp>=0.5);
err0 = err0 + (tmp ~= y(i*50+5*tn+j));
end
end
err0
end 三:结果
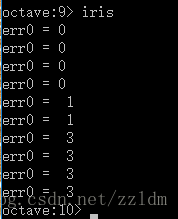
出错的共有三次
四:留1法
%对率回归 iris数据集
%数据集3类数据 A-AX AY-CV CW-ET 各50组
%为了程序读取方便对数据集做了处理1-6 1,2类数据 7-12 1,3类数据 13-18 2,3类数据 A-CV
x = xlsread('E:Program Filesoctaveiris.xlsx', 'Sheet1', 'A52:E151'); %训练数据每次取两类100个
y = xlsread('E:Program Filesoctaveiris.xlsx', 'Sheet1', 'F52:F151');
%数据集分类用了1,2,3来表示 使用不同的类别对y的处理也不同(总之保证y的取值为{0,1})
y = y-1;
k=100;
%留1法
err1=0;%记录错误分类的次数
for tn=1:k
n=0;
old_l=0; %记录上次计算的l
b=[0;0;0;0;1]; %初始参数 (自定义)
while(1)
cur_l=0;
bx=zeros(k,1);
%计算当前参数下的l
for i=1:k
if i == tn %跳过用来检验的样本
continue;
end
bx(i) = b.'*(x(i,:))'; %防止exp函数的参数过大导致无穷大 手动计算
if bx(i)>30
tlog=bx(i);
else
tlog=log(1+exp(bx(i)));
end
cur_l = cur_l - y(i)*bx(i) +tlog;
end
%迭代终止条件
if abs(cur_l-old_l)<0.001
break;
end
n=n+1;
%更新参数(牛顿迭代法)以及保存当前l
old_l = cur_l;
p1=zeros(k,1);
dl=0;
d2l=0;
for i=1:k
if i == tn %跳过用来检验的样本
continue;
end
p1(i) = 1 - 1/(1+exp(bx(i)));
dl = dl - x(i,:)'*(y(i)-p1(i));
d2l = d2l + x(i,:)' * (x(i,:)').'*p1(i)*(1-p1(i));
end
b = b - d2ldl;
end
%用来检验的样本 如果出错则计数+1 每组1个
tmp = 1/(1+exp(-b.'*(x(tn,:))'));
tmp = (tmp>=0.5);
err1 = err1 + (tmp ~= y(tn));
err1
end五:运行结果
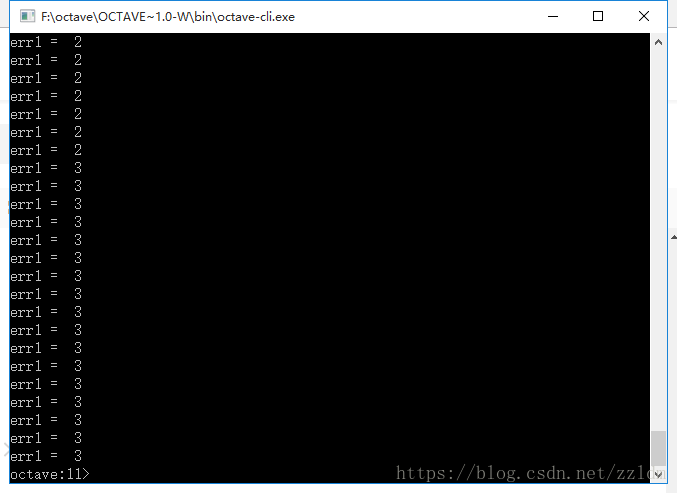
出错的共有三次
来自
最后
以上就是重要楼房最近收集整理的关于机器学习(周志华) 参考答案 第三章 线性模型 3.4的全部内容,更多相关机器学习(周志华)内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复