《机器学习》--周志华（第三章学习笔记）线性模型

65 阅读 0 评论 43 点赞

我是靠谱客的博主踏实柚子，最近开发中收集的这篇文章主要介绍《机器学习》--周志华（第三章学习笔记）线性模型，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

线性模型

基本形式

线性模型试图学得一个通过属性的线性组合来进行预测的函数，即

$f(x) = w_1x_1 + w_2x_2+ ... +w_dx_d +b$

一般用向量形式写成

$f(x) = w^Tx + b$

线性模型形式简单、易于建模，但却蕴涵着机器学习中一些重要的基本思想。

线性回归

线性模型

线性模型试图学得一个通过属性的线性组合来进行预测的函数

$f(x_i) = wx_i + b$

离散属性的处理: 若有 “序”，则连续化；否则，转化为k维向量

令均方误差最小化：
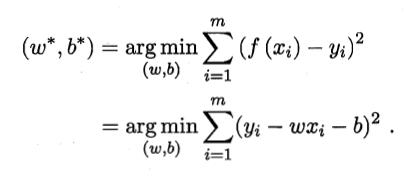
多元线性回归

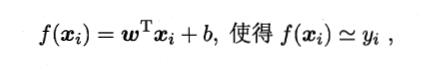
把 $w$ 和 $b$ 吸收入向量形式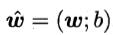数据集表示为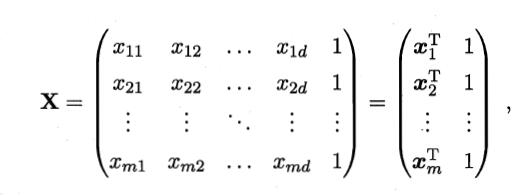

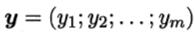
同样采用最小二乘法求解，有
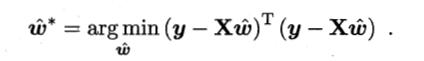
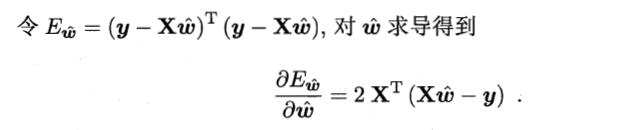
- 若 $X^TX$ 满秩或正定，则
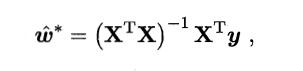
- 若 $X^TX$ 不满秩，则可解出多个 $w$
此时需求助于归纳偏好，或引入正则化

对数线性回归

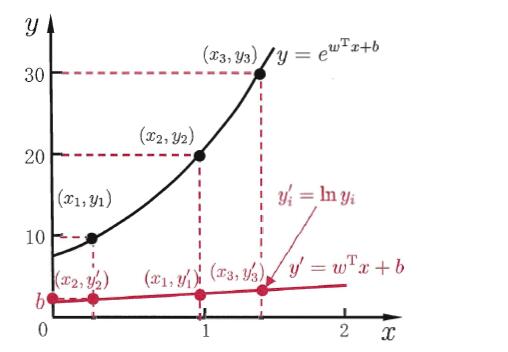
广义线性模型
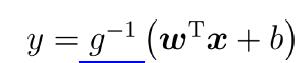
对数几率回归
- 二分类任务
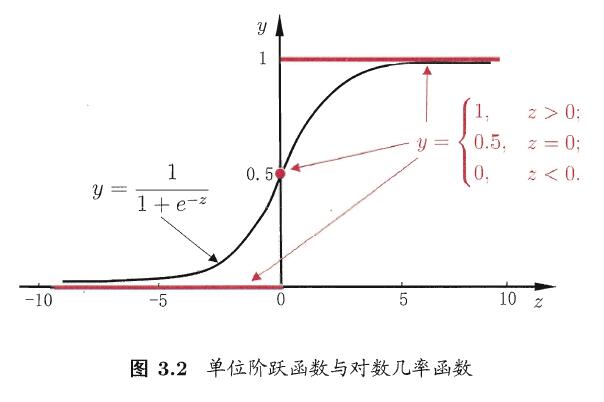
- 对率回归
以对率函数为联系函数

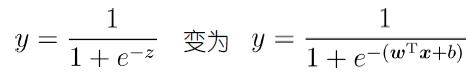
即

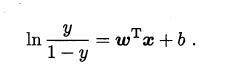
几率，反映了x作为正例的相对可能性

”对数几率回归“亦称“对率回归”
- 无需事先假设数据分布
- 可得到“ 类别” 的近似概率预测
- 可直接应用现有数值优化算法求取最优解
线性判别分析

线性判别分析是一种经典的线性学习方法，在二分类问题上因为最早由Fisher提出，亦称”Fisher 判别分析”。

思想：

给定训练样例集，设法将样例投影到一条直线上，使得同类例的投影点尽可能接近，异类样例的投影点尽可能远离；在对新样品进行分类时，将其投影到相同的这条直线上，在根据投影点的位置来确定新样本的类别。

二维示意图

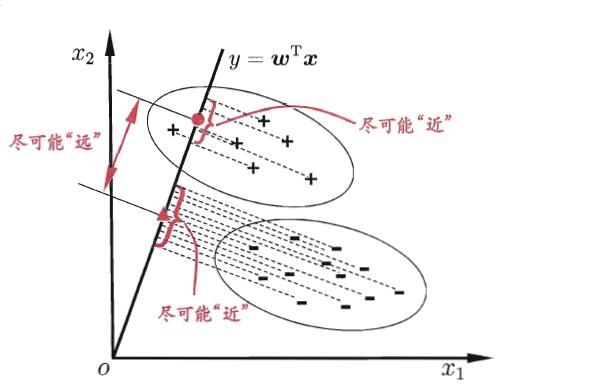
由于将样例投影到一条直线（低维空间），因此也被视为一种“监督降维”技术

LDA的目标

给定数据集

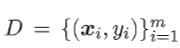
第i类示例的集合 $X_i$

第i类示例的均值向量 $u_i$

第i类示例的协方差矩阵 $E_i$

两类样本的中心在直线上的投影： $w^Tu_0$ 和 $w^Tu_1$

两类样本的协方差： $w^TE_0w$ 和 $w^TE_1w$

同类样例的投影点尽可能接近 -> $w^TE_0w$ + $w^TE_1w$ 尽可能小

异类样例的投影点尽可能远离 -> $||w^Tu_0$ - $w^Tu_1||_2^2$ 尽可能大

于是，最大化

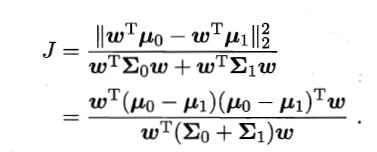
类内散度矩阵

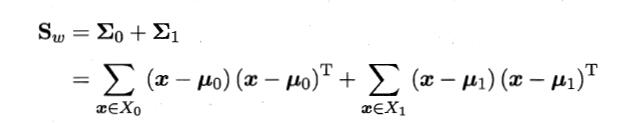
类间散度矩阵

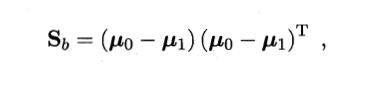
LDA的目标

最大化广义瑞利商
多分类学习

拆解法

将一个多分类任务拆分为若干个二分类任务求解
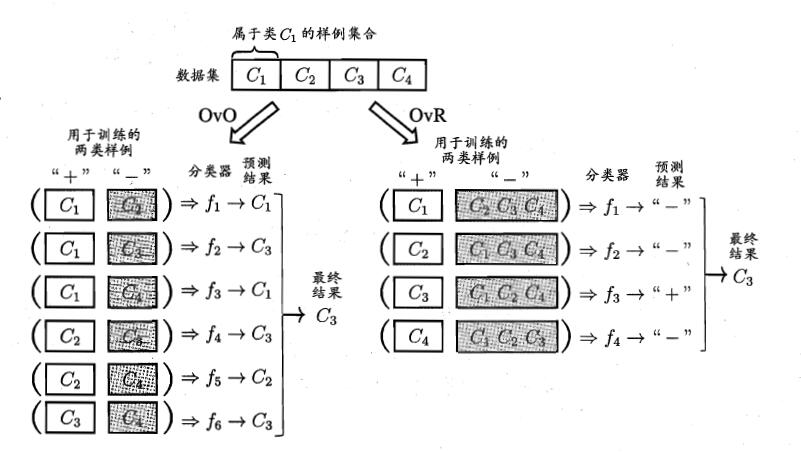
- OvO
- 训练N(N-1)/2个分类器，存储开销和测试时间大
- 训练只用两个类的样例，训练时间短
- OvR
- 训练N个分类器，存储开销和测试时间小
- 训练用到全部训练样例，训练时间长
纠错输出码

多对多：将若干类作为正类，若干类作为反类
- 编码
对N个类别做M次划分，每次划分将一部分类别划为正类，一部分划为反类，从而形成一个二分类训练集；这样一共产生M 个训练集，可以训练出M 个分类器
- 解码
M个分类器分别对测试样本进行预测，这些预测标记组成一个编码，将这个预测编码与每个类别各自的编码进行比较，返回其中距离最小的类别作为最终预测结果。
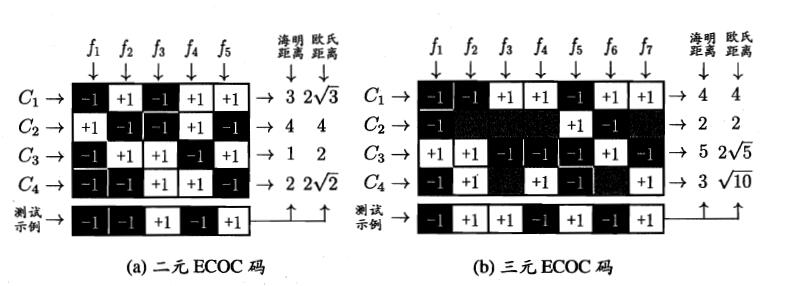
- ECOC编码对分类器错误有一定容忍和修正能力，编码越长，纠错能力越强
- 对同等长度的编码，理论上来说，任意两个类别之间的编码距离越远，则纠错能力越强