机器学习——SVM（支持向量机）

先从一个故事说起

国王为武林高手出了一道题，将红豆绿豆摆在桌子上，让他将其分开，于是武林高手轻松的在桌子上画了一条线，将红豆绿豆分开，如下图

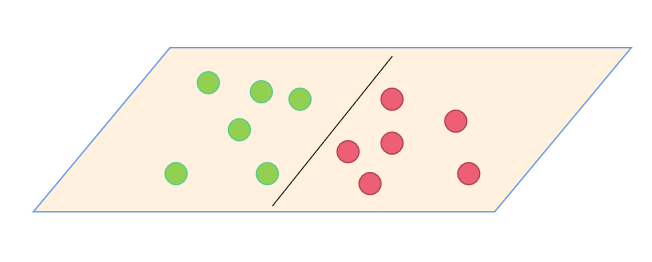
于是，国王又将这两种豆子混子一起散落在桌子上，如图
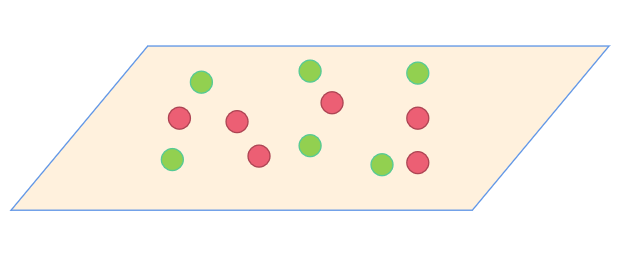又让武林高手将其分开，心想，这次我看你怎么分，没想到，武林高手站在桌子面前，运足内力，用手掌拍在桌子上，豆子瞬间腾空而起，高手用一张纸将豆子分成两部分，上面的是绿豆，下面的是红豆

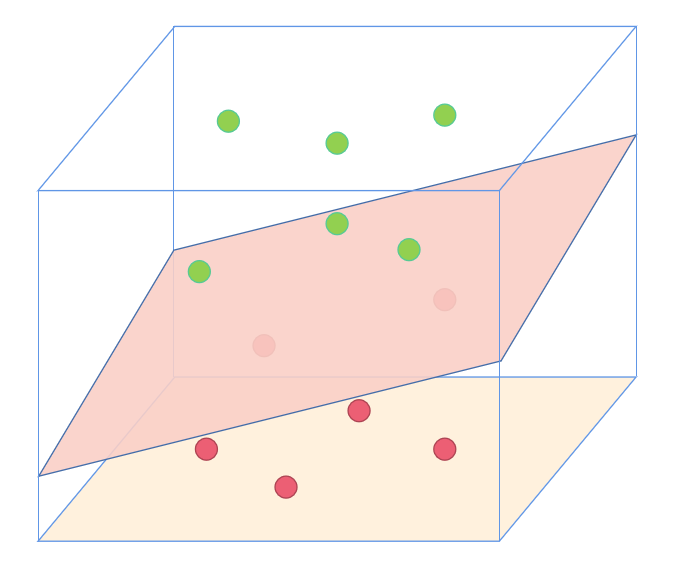
上面的故事其实就是支持向量机的直观理解，这些豆子叫做data，把线叫做classifier, 最大间隙trick叫做optimization，拍桌子叫做kernelling, 那张纸叫做hyperplane

支持向量机( support vector machines， SVM)是一种二类分类模型。SVM最基本的原理就是寻找一个分隔“平面”将样本空间一分为二，对于二维平面，分割的其实是一条线，三维平面就需要一个平面来分开，对于 n 维数据，要想将其分开，就需要一个 n-1 维的超平面

支持向量机学习方法包含构建由简至繁的模型：线性可分支持向量机( linear support vectormachine in linearly separable case)、线性支持向量机( linear support vector machine)及非线性支持向量机(non- linear support vector machine)。 简单模型是复杂模型的基础，也是复杂模型的特殊情况。当训练数据线性可分时， 通过硬间隔最大化( hard margin maximization)，学习一个线性的分类器，即线性可分支持向量机，又称为硬间隔支持向量机；当训练数据近似线性可分时，通过软间隔最大化( soft margin aximization)，也学习一个线性的分类器，即线性支持向量机，又称为软间隔支持向量机；当训练数据线性不可分时，通过使用核技巧( kernel trick)及软间隔最大化，学习非线性支持向量机

硬间隔最大化模型

下面就从线性可分支持向量机硬间隔最大化说起，以二维为例，如图

要把数据分开可以有很多种分法，我们要取得就是最好的分法，如上图，黑色线代表分割直线（平面），蓝色区域代表间隔，显然，间隔越大，代表这个线（面）的区分能力越大。我们的目的就是找到这个线（面），由上图我们可以看到，绝大多数样本对这个间隔的大小不起作用，只有在蓝色区域边上的样本才能决定间隔的大小，SVM中这些落在边缘的样本称为支持向量，这也就是SVM名字的由来

这个分割平面用公式表示
$$w^{T}x+b=0$$
分类决策函数为
$$f(x)=sign(w^{T}x+b)$$
其中 $x$ 表示一个 n 维的样本向量，$w$ 是平面的 n 维法向量。虽然从公式上来看和线性回归很像，但是它们之间的本质区别，线性回归是用来拟合label的，而SVM的平面方程是用来确定平面方向的。在这个平面一侧为一类数据，另一侧则为另一类

我们的目标是让这个间隔最大，样本到这个分割平面的距离为
$$d=\frac{|w^{T}x+b|}{||w||}$$
这个公式其实就是高中学过点到直线距离得演变
$$d=\frac{|Ax+By+C|}{\sqrt{A^2+B^2}}$$
||w|| 是L2范数

模型假设

首先这个平面要将数据正确分类，在平面上方的数据类别为 $y=1$，在平面下方的数据类别为 $y=-1$
对于上方数据，到平面距离 $w^{T}x+b>0$, 平面下方数据 $w^{T}x+b<0$，这样我们可以用
$$y_i(w^T{x}_i+b)>0$$
表示样本被正确分类
这样问题就转化为
$$\{\begin{array}{ll}max& 2\frac{|w^{T}x+b|}{||w||}\\ s.t.& y_i(w^T{x}_i+b)>0,i=1,2,3\dots ，n\end{array}$$
在间隔边缘上的点到分割平面的距离是间隔距离得一半，我们令这个点的函数值为 $\gamma$，则
$$\begin{gathered} y_i(w^T{x}_i+b)=\gamma \\ {y}_i(\frac{w^T}{\gamma }{x}_i+\frac{b}{\gamma })=1 \end{gathered}$$
这里令新的 $\hat{w}=\frac{w^T}{\gamma }$，新的$\hat{b}=\frac{b}{\gamma }$，可以将这个距离看做是单位 1，这样就得到 $y_i(w^T{x}_i+b)\ge 1$ 对于支持向量来说 $y_i(w^T{x}_i+b)=1$，那么间隔可以表示为
$$\gamma =2\frac{|w^{T}x+b|}{||w||}=\frac{2}{||w||}$$
为了方便计算，我们要求$\frac{2}{||w||}$的最大值，转换为 $||w|{|}^2$ 的最小值，问题进一步转化为
$$\{\begin{array}{ll}\underset{w,b}{\min }& \frac{||w|{|}^2}{2}\\ s.t.& y_i(w^T{x}_i+b)\ge 1,i=1,2,3\dots ，n\end{array}$$
目标函数本身是一个凸二次规划问题，能直接用现成的优化计算包求解，这种解法有一个很大的缺点在于没办法套用核函数，我们可以有更高效的做法——求解对偶问题
首先要构造朗格朗日函数
我们先看一下拉格朗日乘子法的使用过程，给定一个不等式约束问题：
$$\{\begin{array}{l}\underset{x}{\min }f(x)\\ \begin{array}{r}s.t.g_i(x)\le 0,i=1,2,3\dots ，k\\ h_i(x)=0,i=1,2,3\dots ，m\end{array}\end{array}$$
我们引入一个广义朗格朗日函数，将它改写成这样：
$$L(x,\alpha ,\beta )=f(x)+\sum _{i=1}^k{\alpha }_i{g}_i(x)+\sum _{i=1}^m{\beta }_i{h}_i(x),{\alpha }_i\ge 0$$
我们会发现 $L\le f(x)$所以我们要求的是 $maxL(x,\alpha ,\beta )$
最终的目标是
$$\underset{b,w}{\min }(\underset{{\alpha }_i\ge 0}{\max }L(b,w,\alpha ))$$
构造的拉格朗日函数为
$$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2+\sum _{i=1}^m{\alpha }_i(1-y_i(w^T{x}_i+b))$$

对偶问题

$\underset{b,w}{\min }(\underset{{\alpha }_i\ge 0}{\max }L(b,w,\alpha ))$ 转化为 $\underset{{\alpha }_i\ge 0}{\max }(\underset{b,w}{\min }L(b,w,\alpha ))$

KKT条件
$$\begin{array}{rl}{\alpha }_i& \ge 0\\ y_i(w^T+b)-1& \ge 0\\ {\alpha }_i(1-y_i(w^T+b))& =0\end{array}$$

分别对 $w,b$求导

$$\begin{array}{rl}& \frac{\partial L}{\partial b}=-\sum _{i=1}^m{\alpha }_i{y}_i=0\\ & \frac{\partial L}{\partial w}=w-\sum _{i=1}^m{\alpha }_i{y}_i{x}_i\to w=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i\end{array}$$
代入到上面函数
$$\begin{array}{rl}L(w,b,\alpha )& =\frac{1}{2}{w}^{T}w+\sum _{i=1}^m{\alpha }_i-\sum _{i=1}^m{\alpha }_i{y}_i{w}^T{x}_i-\sum _{i=1}^m{\alpha }_i{y}_{i}b\\ & =-\frac{1}{2}(\sum _{i=1}^m{\alpha }_i{y}_i{x}_i{)}^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i+\sum _{i=1}^m{\alpha }_i\\ & =\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j\end{array}$$
我们要求的是上式的最大值，最终我们的目标是
$$\underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j-\sum _{i=1}^m{\alpha }_i$$

$$\begin{array}{rl}s.t.& \sum _{i=1}^m{\alpha }_i{y}_i=0\\ & {\alpha }_i\ge 0,i=1,2,3,\dots ,m\end{array}$$
唯一的变量 $\alpha$，求出 $\alpha$ 就可以推导出对应的 $w$ 和 $b$ 了
$$\begin{gathered} w=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i \\ b=y_i-w\ast x_i \end{gathered}$$

软间隔最大化模型

在实际场景中，数据不可能都是线性可分的，我们要允许一些样本出错，这样我们就要引入一个松弛变量 $\xi$，适当放松 $y_i(w^t{x}_i+b)\ge 1$ 这个条件，变为 $y_i(w^t{x}_i+b)\ge 1-\xi$
我们把松弛变量加入到目标函数中
$$\begin{gathered} \begin{array}{rl}\underset{b,w,\xi }{\min }& \frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{\xi }_i\\ & s.t.y_i(w^T{x}_i+b)\ge 1-\xi ,i=1,2,3\dots ，n\end{array} \\ {\xi }_i\ge 0,i=1,2,3\dots n， \end{gathered}$$
C为一个常数，可以理解为惩罚参数。我们希望$||w|{|}^2$尽可能小，也希望$\sum {\xi }_i$尽量小，C就是用来协调两者的。C越大代表我们对模型的分类要求越严格

拉格朗日函数

$$L(w,b,\xi ,\alpha ,\beta )=\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{\xi }_i+\sum _{i=1}^m{\alpha }_i(1-{\xi }_i-y_i(w^T{x}_i+b))+\sum _{i=1}^m{\beta }_i(-{\xi }_i)$$
我们要求这个函数的最值，也就是
$$\underset{w,b,\xi }{\min }(\underset{\alpha \ge 0,\beta \ge 0}{\max }L(w,b,\xi ,\alpha ,\beta ))$$
原函数的对偶问题是
$$\underset{\alpha \ge 0,\beta \ge 0}{\max }(\underset{w,b,\xi }{\min }L(w,b,\xi ,\alpha ,\beta ))$$

分别对 $w,b,\xi$求导

$$\begin{array}{rl}& \frac{\partial L}{\partial w}=w-\sum _{i=1}^m{\alpha }_i{y}_i{x}_i\to w=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i\\ & \frac{\partial L}{\partial b}=-\sum _{i=1}^m{\alpha }_i{y}_i=0\\ & \frac{\partial L}{\partial \xi }=C-{\alpha }_i-{\beta }_i=0\to {\beta }_i=C-{\alpha }_i\end{array}$$
代入对偶函数得：
$$\begin{array}{rl}L(w,b,\xi ,\alpha ,\beta )& =-\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{\xi }_i+\sum _{i=1}^m{\alpha }_i(1-{\xi }_i)-\sum _{i=1}^m(C-{\alpha }_i){\xi }_i\\ & =\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j\end{array}$$
由于 ${\alpha }_i\ge 0$ ，可以得到 $0\le {\alpha }_i\le C$ ,所以最后式子化简为
$$\underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j-\sum _{i=1}^m{\alpha }_i$$

$$\begin{array}{rl}s.t.& \sum _{i=1}^m{\alpha }_i{y}_i=0\\ & 0\le {\alpha }_i\le C,i=1,2,3,\dots ,m\end{array}$$
下面来看KTT条件，分三个部分
原始问题可行：
$$\begin{array}{rl}1-{\xi }_i-y_i(w^T{x}_i+b)& \le 0\\ -{\xi }_i& \le 0\end{array}$$
对偶问题可行：
$$\begin{array}{rl}{\alpha }_i& \ge 0\\ {\beta }_i& =C-{\alpha }_i\end{array}$$
以及松弛可行：
$$\begin{array}{rl}{\alpha }_i(1-{\xi }_i-y_i(w^T{x}_i+b))& =0\\ {\beta }_i{\xi }_i& =0\end{array}$$
观察 ${\alpha }_i(1-{\xi }_i-y_i(w^T{x}_i+b))=0$
1.如果 ${\alpha }_i=0$，则$\beta >0,$ ${\xi }_i=0$ 那么 $1-{\xi }_i-y_i(w^T{x}_i+b)\le 0$，即 $y_i(w^T{x}_i+b)\ge 1$，样本被正确分类，这些样本不是支持向量
2.如果 ${\alpha }_i>0$，那么 $1-{\xi }_i-y_i(w^T{x}_i+b)=0$，样本是支持向量。由于 $C={\alpha }_i+{\beta }_i$
又可以分为下面两种情况
（1）$0<\alpha <C$，那么 ${\beta }_i>0$ ，所以 ${\xi }_i=0$，样本在边界上
（2）$\alpha =C$，那么 ${\beta }_i=0$ ，此时

• 如果 ${\xi }_i<1$，样本被正确分类
• 如果 ${\xi }_i=1$，样本在超平面上
• 如果 ${\xi }_i>1$，样本分类错误

核函数

对于线性不可分的数据集，无法在原始空间找到分离平面，于是我们就要把原始数据映射到更高的维度（如故事中的拍桌子），在高维度上找到一个分割平面。
在线性回归中，我们用多项式扩展可以将非线性问题转化为线性问题，我们借鉴这个思路，在SVM中，我们把低维不可分的数据，映射到高维，变成线性可分的。

我们用 $\Phi$ 来表示核函数，样本经过核函数映射之后，就变为 $\Phi (x)$
$$\underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j-\sum _{i=1}^m{\alpha }_i$$

$$\begin{array}{rl}s.t.& \sum _{i=1}^m{\alpha }_i{y}_i=0\\ & 0\le {\alpha }_i\le C,i=1,2,3,\dots ,m\end{array}$$
把核函数代入便得到
$$\underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j\Phi (x_i{)}^T\Phi (x_j)-\sum _{i=1}^m{\alpha }_i$$

$$\begin{array}{rl}s.t.& \sum _{i=1}^m{\alpha }_i{y}_i=0\\ & 0\le {\alpha }_i\le C,i=1,2,3,\dots ,m\end{array}$$
我们可以看到，核函数仅仅是将內积 $x_i^T{x}_j$ 变成 $\Phi (x_i{)}^T\Phi (x_j)$，如果我们的原始数据是2维度，映射到5维，再做点积运算，复杂度就会大大提高，如果是更高维度，复杂度将会大大增加，而核函数是在低微来计算得，这样就降低了运算的复杂度，我们把符合这种条件的函数称为核函数，称为K
$$K(x_i,x_j)=K(x_i^T{x}_j)=\Phi (x_i{)}^T\Phi (x_j)$$

核函数作用其实就是把问题映射到更高维度，把求解复杂度降下来，在训练模型时如果用到了核函数，在与测试也会经过核函数
经过核函数，数据被映射到高维，计算量只是增加了一点
常用的核函数有
1、线性核函数 $K(x_i,x_j)=x_i^T{x}_j$
2、多项式核函数 $K(x_i,x_j)=(\gamma x_i^T{x}_j+r{)}^d$ 其中 $\gamma ,r,d$需要自己调参
3、高斯核函数 $K(x_i,x_j)=exp(-\gamma ||x_i-x_j|{|}^2)$
4、sigmoid核函数 $K(x_i,x_j)=tanh(\gamma x_i^T{x}_j+r)$ 其中 $\gamma ,r$需要自己调参

最后

以上就是风中画板为你收集整理的机器学习——SVM（支持向量机）的全部内容，希望文章能够帮你解决机器学习——SVM（支持向量机）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。