1.问题描述:
有一个推销员,要到n个城市推销商品,他要找出一个包含所有n个城市的具有最短路程的环路。(最后回到原来的城市)
示例:从城市1出发经过所有城市后回到城市1,要使总路程最短。
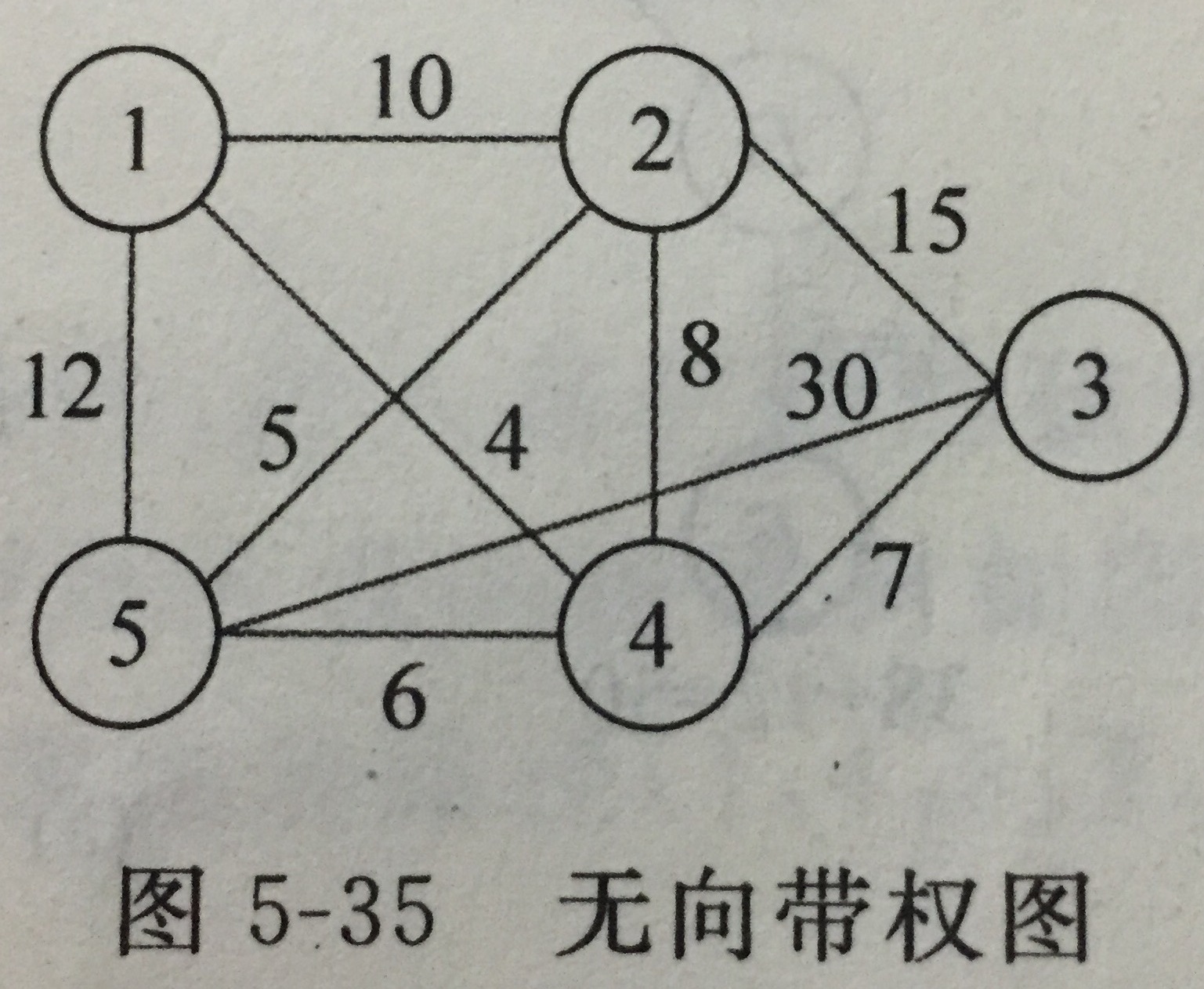
2.1算法设计思想(一):
给定n个城市的无向带权图G(V,E),顶点代表城市,权值代表城市之间的距离。若城市之间没有路径,则距离为无穷。
城市之间的距离存放在二维数组g[][]中。
从城市1出发,先到临近城市2,将走过的路程存放在变量 cl 中。
bestl代表当前找到的一种最短路径长度。如走法:1-2-3-4-5-1
显然,向城市深处走时,cl只会增加。因此当cl>bestl时,不必再往深处走。
限界条件为cl<bestl, cl 初值为0,bestf初值为∞
版本一的算法实现
[cpp] view plain copy
- #include<iostream>
- using namespace std;
- #define MAX 1000
- int g[100][100],x[100],bestx[100];
- int cl=0,bestl=MAX,n;
- void Traveling(int t)
- {
- int j;
- if(t>n) //到达叶子结点
- {
- if(g[x[n]][1]!=-1 && (cl+g[x[n]][1]<bestl))//推销员到的最后一个城市与出发的城市之间有路径,且当前总距离比当前最优值小
- {
- for(j=1; j<=n; j++)
- bestx[j]=x[j];
- bestl=cl+g[x[n]][1];
- }
- }
- else //没有到达叶子结点
- {
- for(j=t; j<=n; j++)//搜索扩展结点的左右分支,即所有与当前所在城市临近的城市
- {
- if(g[x[t-1]][x[j]]!=-1 && (cl+g[x[t-1]][x[j]]<bestl))//若果第t-1个城市与第t个城市之间有路径且可以得到更短的路线
- {
- swap(x[t],x[j]); //保存要去的第t个城市到x[t]中
- cl+=g[x[t-1]][x[t]]; //路线长度增加
- Traveling(t+1); //搜索下一个城市
- cl-=g[x[t-1]][x[t]];
- swap(x[t],x[j]);
- }
- }
- }
- }
- int main()
- {
- int i,j;
- cout<<"请输入一共有几个城市:"<<endl;
- cin>>n;
- cout<<"请输入城市之间的距离"<<endl;
- for(i=1; i<=n; i++)
- for(j=1; j<=n; j++)
- cin>>g[i][j];
- for(i=1; i<=n; i++)
- {
- x[i]=i;
- bestx[i]=0;
- }
- Traveling(2);
- cout<<"城市路线:"<<endl;
- for(i=1; i<=n; i++)
- cout<<bestx[i]<<' ';
- cout<<bestx[1];
- cout<<endl;
- cout<<"最短路线长度:"<<endl;
- cout<<bestl<<endl;
- return 0;
- }
- /*
- 测试数据:
- 5
- -1 10 -1 4 12
- 10 -1 15 8 5
- -1 15 -1 7 30
- 4 8 7 -1 6
- 12 5 30 6 -1
- */
2.2版本实现二(更精确的利用界定函数削减分支)原理具体看北大算法公开课,屈婉玲老师讲的。就是喜欢没有废话的视频课
与网上绝大多数这个问题的解法不同,这个版本的界定函数更准确,也就意味不必要的分支削减更多,算法实际时效更高
搜索树的叶片数:O((n-1)!,每个叶子结点对应一条路径,每条路径n个节点
每个节点的代价函数计算时间O(1),每条路径的计算计算时间O(n)
最坏情况下时间复杂度是O(n!)同蛮力算法
但是实际中,分支限定可以削减许多不必要的搜索分支
//搜索树的叶片数:O((n-1)!,每个叶子结点对应一条路径,每条路径n个节点
//每个节点的代价函数计算时间O(1),每条路径的计算计算时间O(n)
//最坏情况下时间复杂度是O(n!)
//但是实际中,分支限定可以削减许多不必要的搜索分支#include<iostream>
using namespace std;
#define MAX 1000
int g[100][100], x[100], bestx[100];
int cl = 0, bestl = MAX, n;
//界定函数,按照屈婉玲老师的算法公开课视频讲解的给出的实现,这与网上绝大多数版本的界定函数不同,可以更精确的削减分支
double Bound(int t, int cl)
{
double min1 = 0, min2 = 0, tempSum=0;
for (int j = t; j <= n; j++)
{
if (g[x[t - 1]][x[j]] != -1 && g[x[t - 1]][x[j]] < min1)
{
min1 = g[x[t - 1]][x[j]];
}
for (int i = 1; i <= n; ++i)
{
if (g[x[j]][x[i]] != -1 && g[x[j]][x[i]] < min2)
{
min2 = g[x[j]][x[i]];
}
}
tempSum += min2;
}
return cl + min1 + tempSum;
}
void Traveling(int t)
{
int j;
if (t>n) //到达叶子结点
{
if (g[x[n]][1] != -1 && (cl + g[x[n]][1]<bestl))//推销员到的最后一个城市与出发的城市之间有路径,且当前总距离比当前最优值小
{
for (j = 1; j <= n; j++)
bestx[j] = x[j];
bestl = cl + g[x[n]][1];
}
}
else //没有到达叶子结点
{
for (j = t; j <= n; j++)//搜索扩展结点的左右分支,即所有与当前所在城市临近的城市
{
if (g[x[t - 1]][x[j]] != -1 && Bound(t, cl)<bestl)
//if (g[x[t - 1]][x[j]] != -1 && (cl + g[x[t - 1]][x[j]]<bestl))//若果第t-1个城市与第t个城市之间有路径且可以得到更短的路线
{
swap(x[t], x[j]); //保存要去的第t个城市到x[t]中
cl += g[x[t - 1]][x[t]]; //路线长度增加
Traveling(t + 1); //搜索下一个城市
cl -= g[x[t - 1]][x[t]];
swap(x[t], x[j]);
}
}
}
}
int main()
{
int i, j;
cout << "请输入一共有几个城市:" << endl;
cin >> n;
cout << "请输入城市之间的距离" << endl;
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
cin >> g[i][j];
for (i = 1; i <= n; i++)
{
x[i] = i;
bestx[i] = 0;
}
Traveling(2);
cout << "城市路线:" << endl;
for (i = 1; i <= n; i++)
cout << bestx[i] << ' ';
cout << bestx[1];
cout << endl;
cout << "最短路线长度:" << endl;
cout << bestl << endl;
return 0;
}3.算法实现结果:
输入:
|
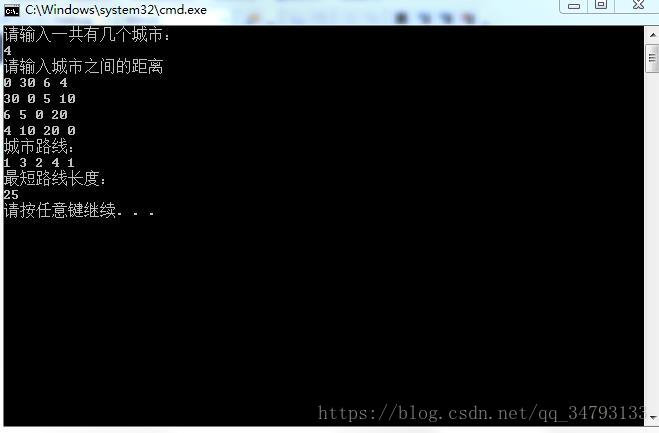
最后
以上就是欣慰薯片最近收集整理的关于回溯算法----货郎(售货员)问题的全部内容,更多相关回溯算法----货郎(售货员)问题内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复