填空题
5-7
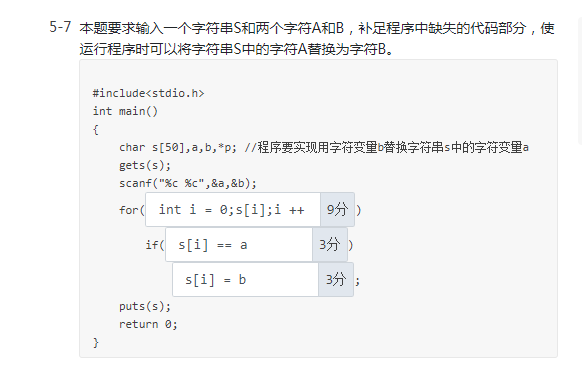
5-8
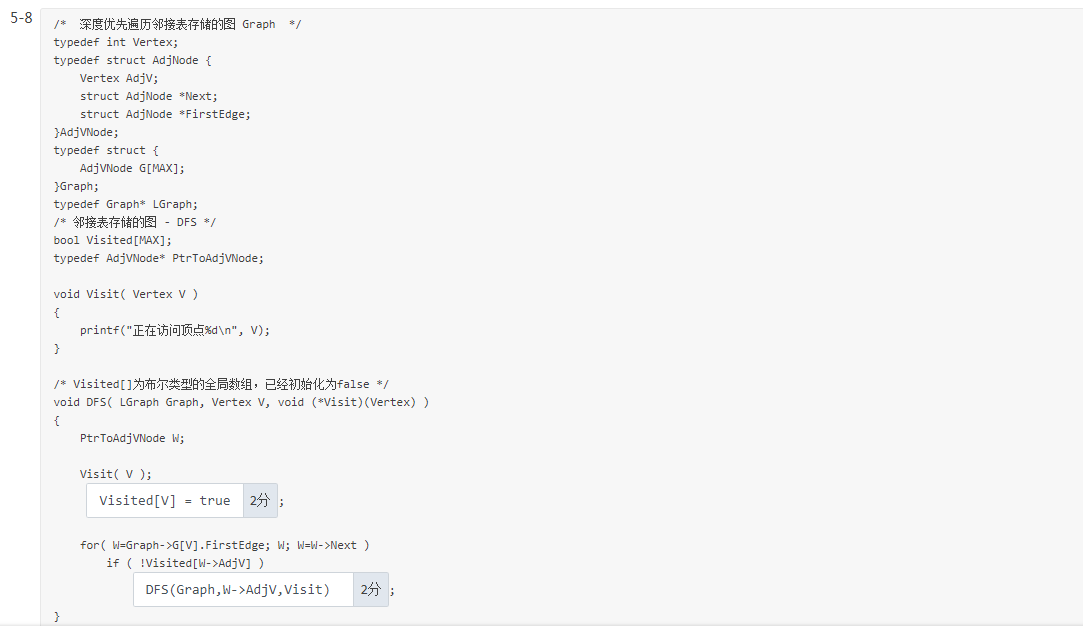
5-9
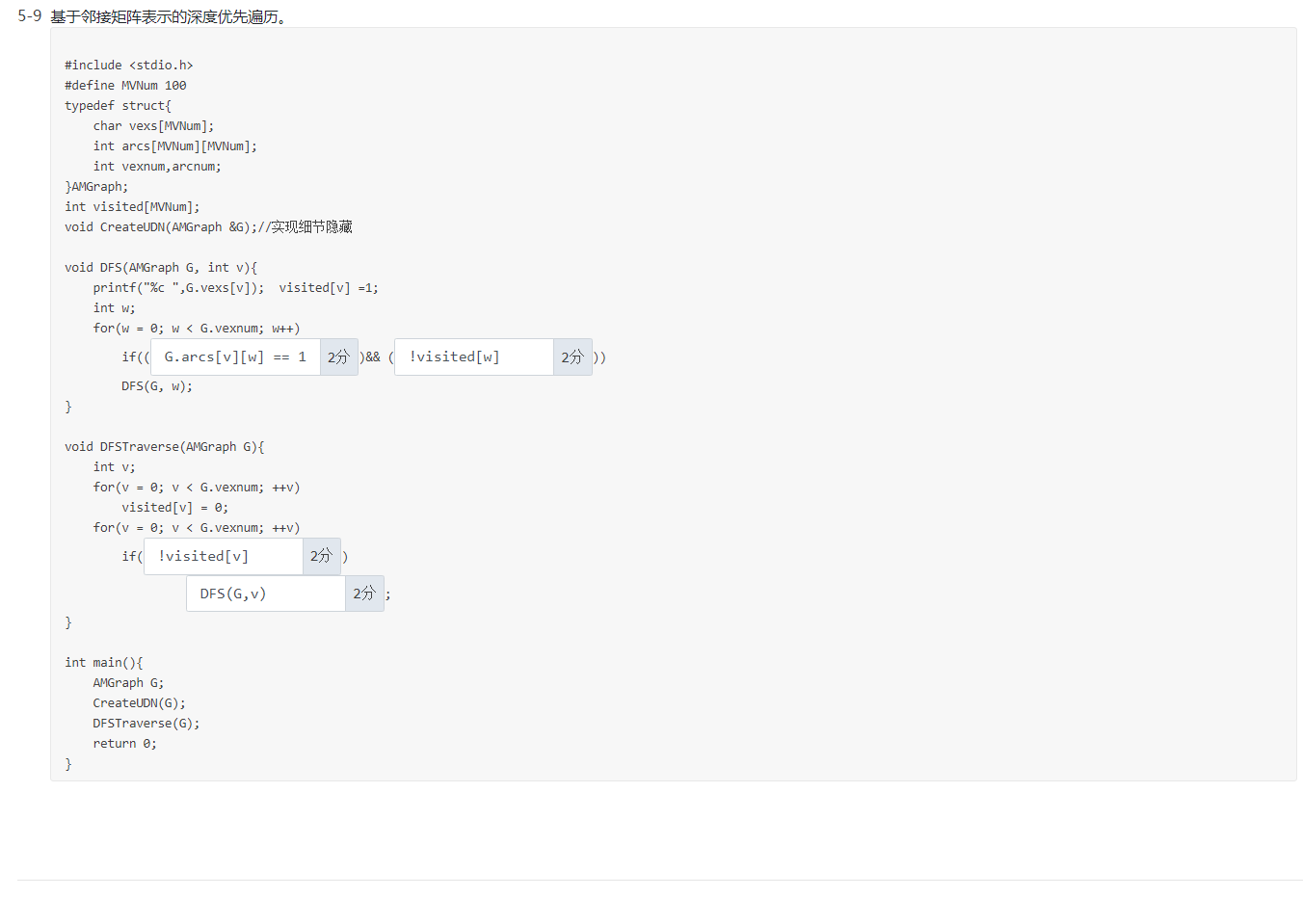
5-10
5-11
5-12
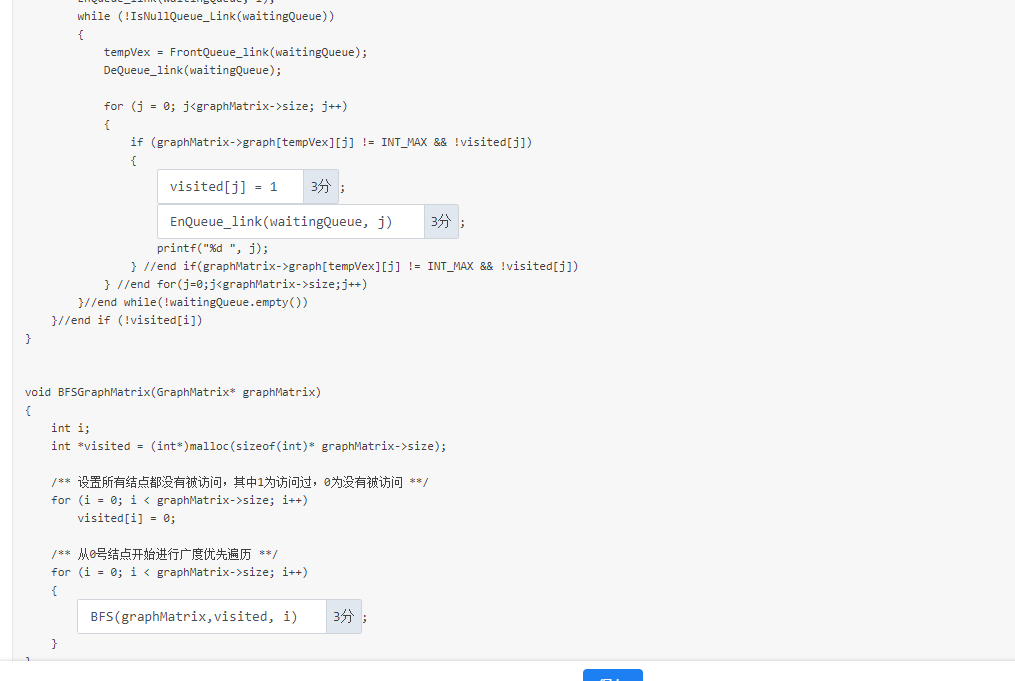
5-13
5-14
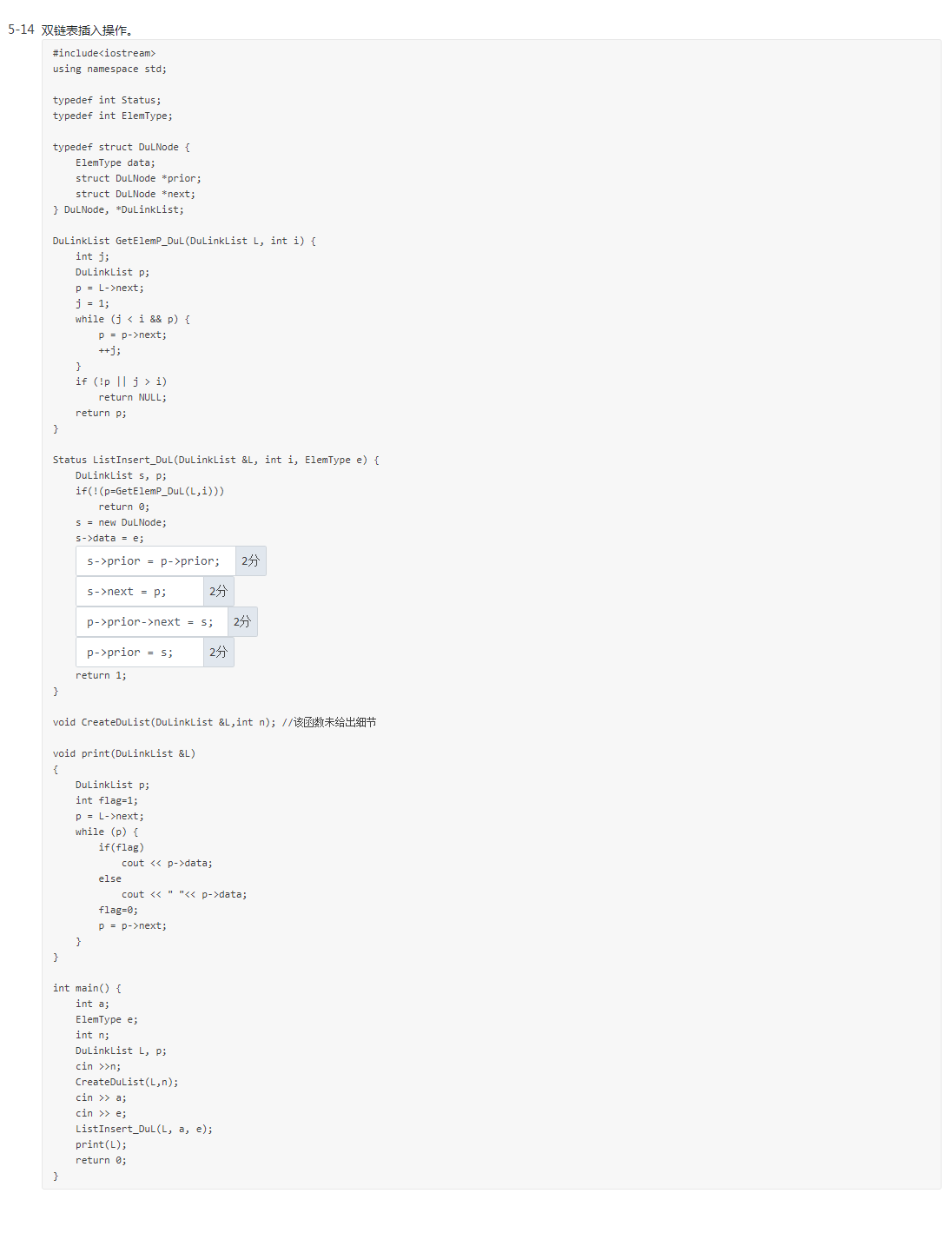
5-15
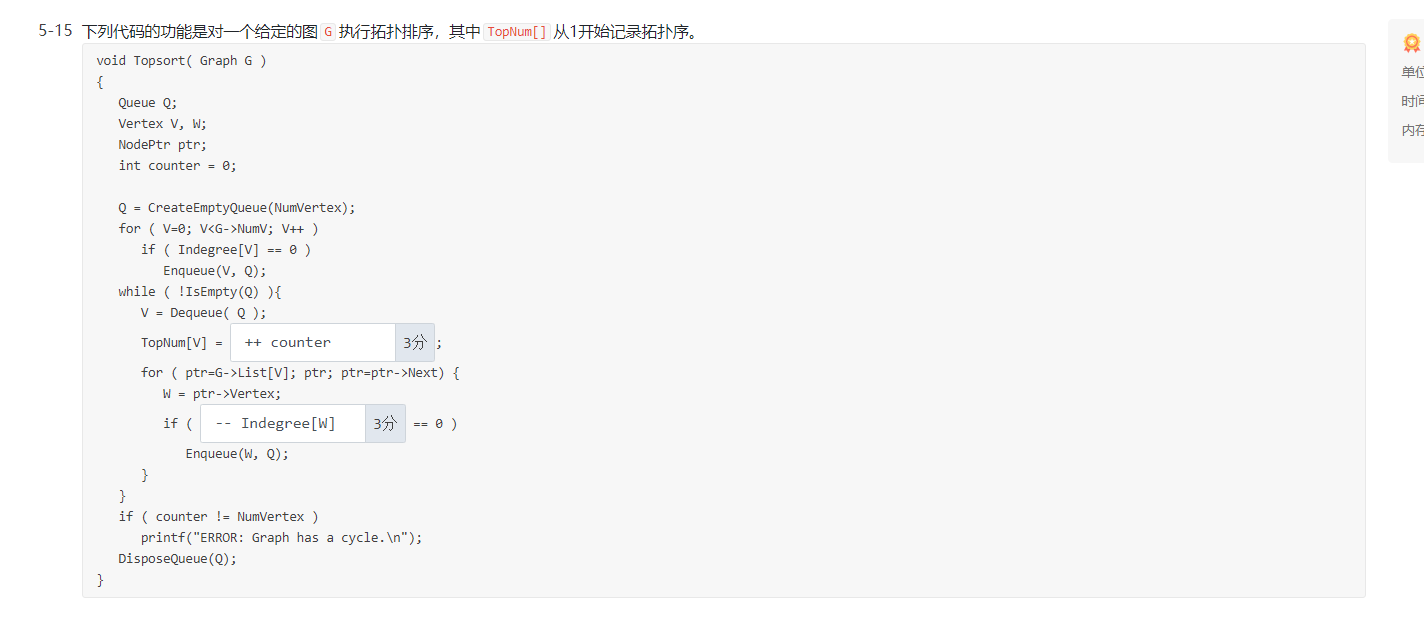
5-16
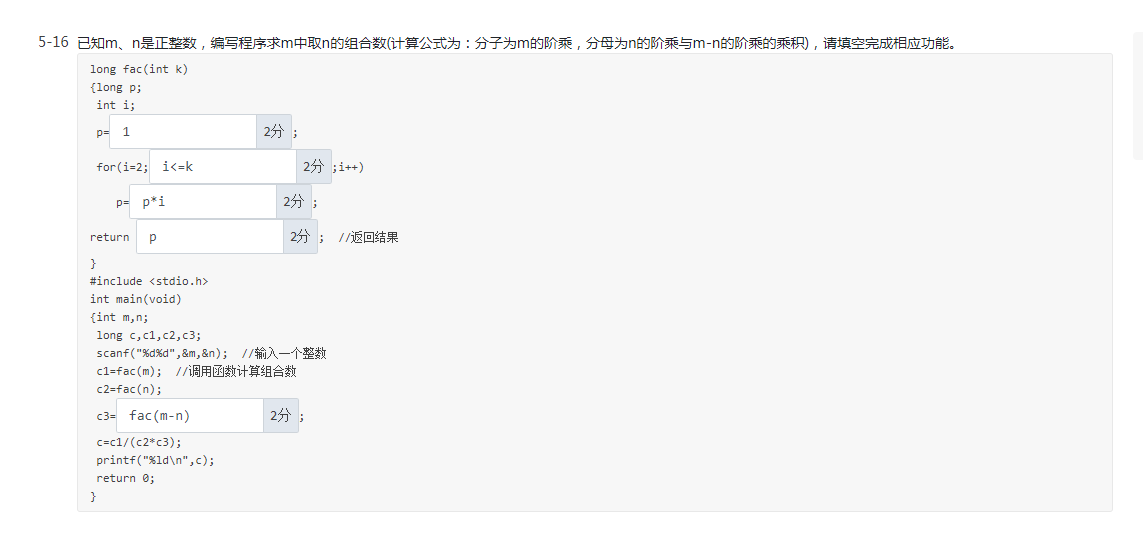
函数题
6-8 字符串比较 (10 分)
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16int fun(char a[],char b[]) { int n = strlen(a); int m = strlen(b); for(int i = 0;i < n && i < m;i ++){ if(a[i] == b[i]) continue; if(a[i] > b[i]) return 1; if(a[i] < b[i]) return -1; } if(n == m) return 0; else if(n > m) return 1; else return -1; }
6-9 模式匹配 (10 分)
复制代码
1
2
3
4
5
6
7
8
9/* s为主串，t为模式串。 * 函数返回t在s中第一次出现的位置。 */ int BF(string s, string t) { // 这是一个string库，find(“t”).,如果找到，则返回位置，找不到,返回-1 return s.find(t); }
6-10 汉诺塔问题 (10 分)
- 2 n − 1 2^{n} - 1 2n−1就是最终答案
复制代码
1
2
3
4
5void hanoi(int n, int a, int b, int c) { count = (1 << n) - 1; }
6-11 背包问题 (10 分)
- 贪心，选取最大的前几个,这个可以选零点几份
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24float Knapsack(int n,float c,float v[],float w[],float x[]) { float ans = 0; for(int i = 1;i <= n;i ++){ x[i] = 0; } for(int i = 1;i <= n;i ++){ if(c >= w[i]){ c -= w[i]; x[i] = 1; ans += v[i]; }else{ ans += v[i] / w[i] * c; x[i] = c / w[i]; break; } } return ans; }
6-12 邻接矩阵存储图的深度优先遍历 (20 分)
- 注意图联通的话是判断是否等于1
复制代码
1
2
3
4
5
6
7
8
9
10
11
12void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex) ) { Visited[V] = true; Visit(V); for(int i = 0;i < MaxVertexNum;i ++){ if(Graph->G[V][i] == 1){ if(Visited[i]) continue; DFS(Graph,i,Visit); } } }
6-13 基于邻接表表示的广度优先遍历 (20 分)
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18void BFS(ALGraph G, int v) { int q[MAXQSIZE]; int hh = 0,tt = -1; q[++ tt] = v; while(hh <= tt){ int t = q[hh ++]; if(visited[t]) continue; visited[t] = true; printf("%c ",G.vertices[t].data); for(auto p = G.vertices[t].firstarc;p != NULL;p = p->nextarc){ int pp = p->adjvex; if(visited[pp]) continue; q[++ tt] = pp; } } }
6-14 实现基于邻接矩阵表示的深度优先遍历 (20 分)
复制代码
1
2
3
4
5
6
7
8
9
10
11
12void DFS(Graph G, int v) { visited[v] = true; printf("%c ",G.vexs[v]); for(int i = 0;i < G.vexnum;i ++){ if(G.arcs[v][i] == 1){ if(visited[i]) continue; DFS(G,i); } } }
6-15 有序数组的插入 (20 分)
- 注意在最后插入一个元素
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23bool Insert( List L, ElementType X ) { if(L->Last >= MAXSIZE - 1) return false; int n = L->Last; for(int i = 0;i <= n;i ++){ if(L->Data[i] == X) return false; if(L->Data[i] < X){ L->Last ++; for(int j = L->Last;j > i;j --){ L->Data[j] = L->Data[j - 1]; } L->Data[i] = X; return true; } } L->Last ++; L->Data[L->Last] = X; return true; }
6-16 单链表插入排序 (15 分)
- 一不小心把上面那两个函数也实现了
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52/*void CreateListR(LinkNode *&L, ElemType a[], int n) { LinkNode* p = new LinkNode; p->next = NULL; L = p; LinkNode*p1 = new LinkNode; p1->data = a[0]; p1->next = NULL; L->next = p1; p = p1; for(int i = 1;i < n;i ++){ LinkNode*p1 = new LinkNode; p1->data = a[i]; p1->next = NULL; p->next = p1; p = p1; } } //输出线性表,细节不表 void DispList(LinkNode *L) { for(auto t = L->next;t;t = t->next){ printf(" %d",t->data); } } */ //单链表插入排序：元素递增排序 void insertion_sort(LinkNode *&L) { LinkNode*p,*q; int flag_swap; if(!L->next) return; do{ flag_swap = 0; p = L; while(p->next->next){ if(p->next->data > p->next->next->data){ flag_swap ++; q = p->next; p->next = p->next->next; q->next = q->next->next; p->next->next = q; } else p = p->next; } }while(flag_swap > 0); }
6-17 折半插入排序 (10 分)
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17void BInsertSort(SqList &L) { int n = L.length; for(int j = 1;j <= n;j ++){ int p = j; for(int i = j + 1; i <= n;i ++){ if(L.r[p].key > L.r[i].key){ p = i; } } int t = L.r[j].key; L.r[j].key = L.r[p].key; L.r[p].key = t; } }
6-18 拓扑排序 (10 分)
- 注意用stack，用queue是错的(其实一般都用queue)
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40void FindInDegree(ALGraph G,int indegree[]) { for(int i = 0;i < G.vexnum;i ++){ indegree[i] = 0; } for(int i = 0;i < G.vexnum;i ++){ for(auto p = G.vertices[i].firstarc;p != NULL; p = p->nextarc){ indegree[p->adjvex]++; } } } int TopologicalSort(ALGraph G , int topo[]) { int *indegree = new int [G.vexnum + 10]; FindInDegree(G,indegree); int tt = 0; int stk[MVNum]; for(int i = 0;i < G.vexnum;i ++){ if(indegree[i] == 0){ stk[++ tt] = i; } } int cnt = 0; while(tt){ auto t = stk[tt]; tt --; topo[cnt ++] = t; for(auto p = G.vertices[t].firstarc;p != NULL; p = p->nextarc){ indegree[p->adjvex] --; if(indegree[p->adjvex] == 0){ stk[++ tt] = p->adjvex; } } } return cnt == G.vexnum; }
6-19 求解逆序数问题（分治法） (10 分)
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27int tmp[100000]; void Merge(int q[],int l,int mid,int r) { int k = 0, i = l, j = mid + 1; while (i <= mid && j <= r) if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ]; else { ans += mid - i + 1; tmp[k ++ ] = q[j ++ ]; } while (i <= mid) tmp[k ++ ] = q[i ++ ]; while (j <= r) tmp[k ++ ] = q[j ++ ]; for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j]; } void mergesort(int a[],int low,int high) { if(low >= high) return; int mid = low + high >> 1; mergesort(a,low,mid); mergesort(a,mid + 1,high); Merge(a,low,mid,high); // Merge(a,low,mid + 1,high); }
编程题
7-11 串的模式匹配 (30 分)
- 字符串hash，kmp也可以做
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65#include <bits/stdc++.h> using namespace std; const int N = 1e6 + 10; typedef unsigned long long ULL; ULL P = 131; char str[N]; ULL h[N], p[N]; // h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64 // 初始化 // 计算子串 str[l ~ r] 的哈希值 ULL get(int l, int r) { return h[r] - h[l - 1] * p[r - l + 1]; } char str1[N]; ULL h1[N], p1[N]; // h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64 // 初始化 // 计算子串 str[l ~ r] 的哈希值 ULL get1(int l, int r) { return h1[r] - h1[l - 1] * p1[r - l + 1]; } int main() { cin >> str + 1; cin >> str1 + 1; int n = strlen(str + 1); int m = strlen(str1 + 1); if(n < m) { cout << 0 << endl; return 0; } p[0] = 1; for (int i = 1; i <= n; i ++ ) { h[i] = h[i - 1] * P + str[i]; p[i] = p[i - 1] * P; } p1[0] = 1; for (int i = 1; i <= m; i ++ ) { h1[i] = h1[i - 1] * P + str1[i]; p1[i] = p1[i - 1] * P; } ULL l2 = get1(1,m); //cout << l2 << ' ' << m << endl; for(int i = 1;i <= n - m + 1;i ++){ // cout << get(i,i + m - 1) << endl; if(get(i,i + m - 1) == l2){ cout << i << endl; return 0; } } cout << 0 << endl; return 0; }
7-12 字符串模式匹配 (5 分)
- 在上面输出ne数组，在下面是不对的
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38#include <bits/stdc++.h> using namespace std; const int N = 1e6+10; char s[N],p[N]; int ne[N]; int main() { scanf("%s",s+1); scanf("%s",p+1); int n = strlen(s+1); int m = strlen(p+1); int f = -1; printf("%d ",ne[1]-1); for (int i = 2 , j = 0 ; i <= m ; i ++ ) { while(j && p[i] != p[j+1]) j = ne[j]; if(p[i] == p[j+1]) j ++ ; ne[i] = j; printf("%d ",ne[i]-1); } for (int i = 1 , j = 0 ; i <= n ; i ++ ) { while(j && s[i] != p[j+1]) j = ne[j]; if(s[i] == p[j+1]) j ++ ; if(j == m) { f = i - m; break; } } printf("n"); printf("%dn",f); return 0; }
7-13 图深度优先遍历 (10 分)
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43#include <bits/stdc++.h> using namespace std; const int N = 1e6 + 10; typedef unsigned long long ULL; vector<int>v[N]; vector<int>ans; bool st[N]; void dfs(int p){ ans.push_back(p); for(auto &x : v[p]){ if(st[x]) continue; st[x] = true; dfs(x); } } int main() { int n,m; cin >> n >> m; for(int i = 0;i < m;i ++){ int a,b; cin >> a >> b; v[a].push_back(b); } for(int i = 0;i < n;i ++){ sort(v[i].begin(),v[i].end()); } for(int i = 0;i < n;i ++){ if(st[i]) continue; st[i] = true; dfs(i); } // dfs(0); for(auto &x : ans){ cout << x << ' '; } return 0; }
7-14 图的先深搜索 (15 分)
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50#include <bits/stdc++.h> using namespace std; const int N = 1e6 + 10; typedef unsigned long long ULL; int h[N],e[N],ne[N],idx; void add(int a,int b){ e[idx] = b,ne[idx] = h[a],h[a] = idx ++; } bool st[N]; vector<int>ans; void dfs(int p,int fa) { ans.push_back(p); for(int i = h[p];~i;i = ne[i]){ int j = e[i]; if(st[j] || j == fa) continue; st[j] = true; dfs(j,p); } } int main() { memset(h,-1,sizeof h); int n,m,s; cin >> n >> m >> s; for(int i = 0;i < m;i ++){ int a,b; cin >> a >> b; add(a,b); add(b,a); } st[s] = true; dfs(s,0); for(auto &x: ans){ cout << x << ' '; } cout << endl; if(ans.size() != n) cout << 0 << endl; return 0; }
7-15 迷宫-广度策略 (80 分)
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52#include <bits/stdc++.h> using namespace std; const int N = 1100; typedef pair<int,int> PII; int g[N][N]; int dx[] = {0,1,1,1,0,-1,-1,-1}; int dy[] = {1,1,0,-1,-1,-1,0,1}; int fx,fy,sx,sy; int n; PII pre[N][N]; bool st[N][N]; void bfs() { queue<PII> q; q.push({sx,sy}); pre[sx][sy] = {-1,-1}; while(q.size()){ auto t = q.front(); q.pop(); int x = t.first,y = t.second; for(int i = 0;i < 8;i ++){ int a = x + dx[i],b = y + dy[i]; if(a < 0 || a >= n || b < 0 || b >= n) continue; if(g[a][b] || st[a][b]) continue; st[a][b] = true; pre[a][b] = t; if(t.first == fx && t.second == fy) return; q.push({a,b}); } } } void dfs(int x,int y) { cout << x << ' ' << y << ';'; if(x == sx && y == sy) return; dfs(pre[x][y].first,pre[x][y].second); } int main() { cin >> n; for(int i = 0;i < n;i ++) for(int j = 0;j < n;j ++) cin >> g[i][j]; cin >> sx >> sy >> fx >> fy; bfs(); dfs(fx,fy); return 0; }
7-16 图的先广搜索 (15 分)
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56#include <bits/stdc++.h> using namespace std; const int N = 1e6 + 10; typedef unsigned long long ULL; int h[N],e[N],ne[N],idx; void add(int a,int b){ e[idx] = b,ne[idx] = h[a],h[a] = idx ++; } bool st[N]; vector<int>ans; void bfs(int p) { queue<int>q; q.push(p); while(q.size()) { auto t = q.front(); q.pop(); ans.push_back(t); for(int i = h[t];~i;i = ne[i]){ int j = e[i]; if(st[j]) continue; st[j] = true; q.push(j); } } } int main() { memset(h,-1,sizeof h); int n,m,s; cin >> n >> m >> s; for(int i = 0;i < m;i ++){ int a,b; cin >> a >> b; add(a,b); add(b,a); } st[s] = true; bfs(s); for(auto &x: ans){ cout << x << ' '; } cout << endl; if(ans.size() != n) cout << 0 << endl; return 0; }
7-17 插入排序还是归并排序 (25 分)
- 参考
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83#include <bits/stdc++.h> using namespace std; const int N = 1100; int n; int a[N]; int c[N]; int b[N]; bool check(int a[],int b[]){ for(int i = 1;i <= n;i ++){ if(a[i] != b[i]) return false; } return true; } void insertsort() { bool flag = false; for(int i = 2;i <= n;i ++){ sort(a + 1,a + 1 + i); if(flag){ cout << "Insertion Sort" << endl; for(int i = 1;i <= n;i ++){ if(i == n) cout << a[i]; else cout << a[i] << ' '; } return; } if(check(a,b)){ flag = true; } } } void mergesort() { bool flag = false; for(int i = 2;;i *= 2){ for(int j = 0;j < n;j += i){ int r = j + i; if(r > n) r = n; sort(c + 1 + j,c + 1 + r); } if(flag){ cout << "Merge Sort" << endl; for(int i = 1;i <= n;i ++){ if(i == n) cout << c[i]; else cout << c[i] << ' '; } return; } if(check(c,b)){ flag = true; } if(i > n) return; } } int main() { cin >> n; for(int i = 1;i <= n;i ++) { cin >> a[i]; c[i] = a[i]; } for(int i = 1;i <= n;i ++) cin >> b[i]; insertsort(); mergesort(); return 0; }
7-18 插入排序还是堆排序 (25 分)
- 百度
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51#include <iostream> using namespace std; const int N = 110; int n; int a[N], b[N]; void down(int u, int size) { int t = u; if (u * 2 <= size && b[t]<b[u * 2]) t = u * 2; if (u * 2 + 1 <= size && b[t]<b[u * 2 + 1]) t = u * 2 + 1; if (t != u) { swap(b[t], b[u]); down(t, size); } } int main() { cin >> n; for (int i = 1; i <= n; i++) cin >> a[i]; for (int i = 1; i <= n; i++) cin >> b[i]; int p = 2; while (p <= n && b[p] >= b[p - 1]) p++; int k = p; while (p <= n && a[p] == b[p]) p++; if (p == n + 1)//说明是插入排序 { cout << "Insertion Sort" << endl; while (k>1 && b[k]<b[k - 1]) swap(b[k], b[k - 1]), k--; } else //否则说明一定是堆排序 { cout << "Heap Sort" << endl; p = n; while (b[1] <= b[p]) p--; swap(b[1], b[p]); down(1, p - 1); } cout << b[1]; for (int i = 2; i <= n; i++) cout << ' ' << b[i]; cout << endl; return 0; }
7-19 判断一个有向图是否能够完成拓扑排序 (90 分)
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51#include <bits/stdc++.h> using namespace std; const int N = 1e6 + 10; int h[N],e[N],ne[N],idx; void add(int a,int b){ e[idx] = b,ne[idx] = h[a],h[a] = idx ++; } bool st[N]; int din[N]; int n; bool topsort() { queue<int>q; for(int i = 0;i <= n;i ++){ if(!din[i]) q.push(i); } int cnt = 0; while(q.size()){ auto t = q.front(); cnt ++; q.pop(); for(int i = h[t];~i;i = ne[i]){ int j = e[i]; din[j] --; if(din[j] == 0){ q.push(j); } } } return cnt == n + 1; } int main() { memset(h,-1,sizeof h); int a,b; while(cin >> a >> b){ if(a == -1 && b == -1) break; add(a,b); din[b] ++; n = max({a,b,n}); } cout << topsort() << endl; return 0; }
7-20 全排列 (30 分)
- 康托展开，逆康托展开
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55#include <iostream> #include <algorithm> #include <cstring> using namespace std; typedef long long LL; LL fact(LL x) { LL res = 1; for (LL i = 2; i <= x; ++ i) res *= i; return res; } string uncantor(int n, LL inx) // 求在长度为n的序列中，从小到达排列，排第inx的序列是多少(从1开始) { string res; int vis[n * n]; memset(vis, 0, sizeof vis); -- inx; // 比当前序列小的序列有inx个 for (int i = (n - 1); ~i; -- i) { LL c = inx / fact(i), s = inx % fact(i); LL cnt = 0, num; for (LL j = 1; j <= n; ++ j) { if (!vis[j]) ++ cnt; if (cnt == c + 1) // 找到第c+1小的数 { num = j; break; } } vis[num] = 1; res += to_string(num); res += ' '; inx = s; } res.pop_back(); return res; } int main() { LL t; cin >> t; while(t --){ LL n,m; cin >> n >> m; cout << uncantor(n, m) << endl; } return 0; }
最后
以上就是安详鸵鸟最近收集整理的关于作业3填空题函数题编程题的全部内容，更多相关作业3填空题函数题编程题内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复