递归分治 — 例题3.合并排序
一.问题描述
将n个元素排成非递减顺序
二.解题思路
若n为1,算法终止;否则,将n个待排元素分割成k(k=2)个大致相等子集合A,B,对每一个子集合分别递归排序
再将排好序的子集归并为一个集合
合并排序算法可递归地描述如下:
template<class Type>
void MergeSort(Type a[], int left, int right)
{
if(left < right) //至少有两个元素
{
int i = (left+right)/2; //取中点
MergeSort(a, left, i);
MergeSort(a, i+1, right);
Merge(a, b, left, i, right); //合并到数组b
Copy(a, b, left, right); //复制回数组a
}
}
事实上,算法MergeSort的递归过程(自顶向下)只是将待排序集合一分为二,直至待排序集合只剩下一个元素为止,然后不断合并两个排好序的数组段.
所以,我们可以先将数组a中相邻元素两两配对,用合并算法将它们排序,构成n/2组长度为2的排好序的子数组段,再将它们排序成长度为4的排好序的子数组段.如此不断继续,直至整个数组排好序.
按此思想,消去递归后的合并排序算法可描述如下(仅介绍思想):
template<class Type>
void MergeSort(Type a[], int n)
{
Type *b = new int[n];
int s = 1;
while(s < n)
{
MergePass(a, b, s, n); //合并到数组b
s += s;
MergePass(b, a, s, n); //合并到数组a
s += s;
}
}
其中,MergePass()用于合并排好序的相邻数组段.具体的合并算法由Merge()函数来实现.
递归算法的完整代码如下:
#include<bits/stdc++.h>
using namespace std;
int a[50], b[50];
template <class T>
void Merge(T nums[], T nums2[], int left, int i, int right);
void Copy(int *nums, int *nums2, int , int ); //函数提前声明
template <class T>
void MergeSort(T nums[], int left, int right)
{
static int count = 1;
if(left<right) //至少有两个元素
{
int m = (left+right)/2; //取中间位置
cout<<"第"<<count++<<"次划分, left值为:"<<left<<" m值为:"<<m<<" right值为:"<<right<<endl;
MergeSort(nums, left, m);
MergeSort(nums, m+1, right);
Merge(nums, b, left, m, right); //核心,用Merge函数来实现排序.
Copy(nums, b, left, right);
}
}
template <class T>
void Merge(T c[], T d[], int l, int m, int r)
{
static int count = 1;
cout<<"第"<<count++<<"次合并,left值为:"<<l<<" m值为:"<<m<<" right值为:"<<r<<endl;
// 把c[l:m], c[m+1:r]归并到d[l:r]
int i = l, //第一段的游标
j = m+1, //第二段的游标
k = l; //结果的游标
//只要段中存在i和j,则不断进行归并
while((i<=m) && (j<=r))
{
if(c[i]<=c[j])
d[k++] = c[i++];
else
d[k++] = c[j++];
}
//考虑余下的部分
if(i>m) //右半部分还有剩余
{
for(int q=j; q<=r; q++)
d[k++] = c[q];
}
else
{
for(int q=i; q<=m; q++)
d[k++] = c[q];
}
// for(i=l; i<=r; i++) //如果mergesort中不要copy这一个,则需要在这里添加此代码
// {
// c[i] = d[i];
// }
}
void Copy(int *nums, int *nums2, int left, int right)
{
for(int i=left; i<=right; i++)
nums[i] = nums2[i];
}
int main()
{
int n, num;
while(cin>>n )
{
for(int i=0; i<50; ++i) a[i] = b[i] = 0;
for(int i=0; i<n; ++i)
cin>>a[i];
MergeSort(a, 0, n-1); //记住一定是n-1, 因为<=right,=====!!!!!
for(int i=0; i<n; ++i)
cout<<a[i]<<" ";
cout<<endl;
}
system("pause");
return 0;
}
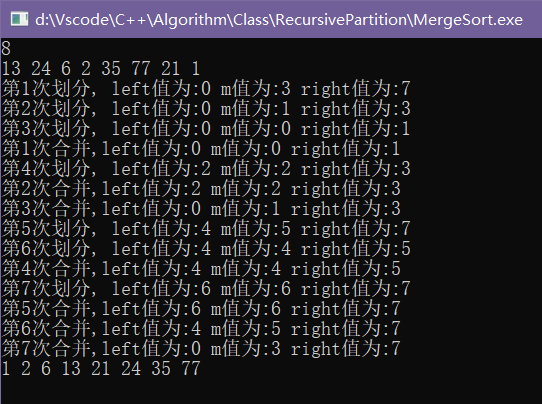
运行结果:
本篇文章参考毕方明老师《算法设计与分析》课件.
欢迎大家访问我的个人博客乔治的编程小屋,和我一起体验养成式程序员的打怪升级之旅吧!
最后
以上就是魁梧项链最近收集整理的关于递归分治 --- 例题3.合并排序的全部内容,更多相关递归分治内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复