概述
浮点数
IEEE浮点数表示
( − 1 s ) ∗ M ∗ 2 E (-1^s) * M * 2^E (−1s)∗M∗2E
-
符号
-
尾数：1~2- ϵ epsilon ϵ 或 0~1- ϵ epsilon ϵ
-
阶码：2的幂
-
单精度浮点数
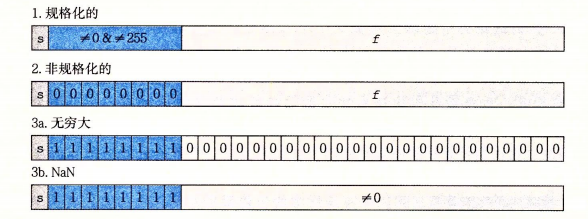
非格式化数
- 提供一种表示0的方法
- 表示那些非常接近于0.0的数
舍入
- 向偶数舍入：向最接近的值舍入
- 中间值：向下或向上舍入，使得结果的最低有效数字是偶数
- 向零舍入：正数向下舍入，负数向上舍入
- 向下舍入
- 向上舍入
浮点运算
- 可交换
- 不满足结合
- 有逆元
- 与NaN运算都是NaN
- 除了NaN，若 a ≥ b age b a≥b ，则 x + a ≥ x + b x + a ge x + b x+a≥x+b
- 舍入
- 不满足乘法分配
- 除了NaN,若 a ≥ b a ge b a≥b且 c ≥ 0 c ge 0 c≥0,则 a ∗ c ≥ b ∗ c a * c ge b * c a∗c≥b∗c;若 a ≥ b a ge b a≥b且 c ≤ 0 c le 0 c≤0,则 a ∗ c ≤ b ∗ c a * c le b * c a∗c≤b∗c
- 除了NaN， a ∗ a ≥ 0 a * a ge 0 a∗a≥0
最后
以上就是现代石头为你收集整理的浮点数 IEEE表示 舍入 运算浮点数的全部内容，希望文章能够帮你解决浮点数 IEEE表示 舍入 运算浮点数所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复