智能驾驶LQR横向控制算法

1. 控制系统

        这里我们先介绍常用的控制系统逻辑：

        假设我们现在状态是x0，我们有状态方程 : 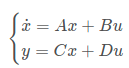                （u为控制矩阵）

        特别的，这里我们是对偏差建立方程，x是偏差的状态，优化的目的是x=0，针对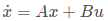我们通过一些假设可以得到详细的方程，这里我直接先给出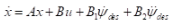其中,  

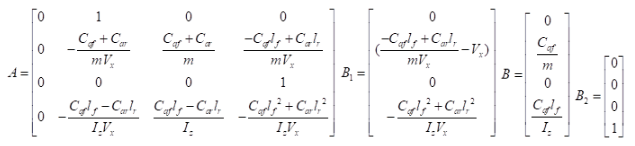
        详细的推导省略，可自行检索。

        再假设有一个反馈控制器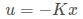：                  这里很重要，可以认为是当前的控制量是通过当前的状态量计算出来的。

        通过这套方法，我们就能得到一个稳定的系统 ：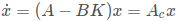  

        当然这是基本的理论，再进一步，我们就会思考，通过这些控制量作为自变量，再设计一个代价函数，来优化这些控制量？

2. LQR控制算法

        讲到这里就很自然引出LQR了，首先的问题代价函数是什么？一方面我们希望系统达到稳定状态，及偏差最小; 另一方面我们希望控制量较小，即付出较小的代价达到我们的目的。这里我直接给出：

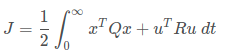
         其中x为状态量，u为控制量，Q为状态权重矩阵，R为控制权重矩阵。

          特别的x和u中取值有正有负，所以需要平方和最小，在矩阵中没有平方，这里我们采用转置乘以本身的做法模拟矩阵的平方，如x^T*x 。这里状态量x和控制量u都是多维向量，上式计算的结果是一个标量。

          其实我们可以把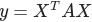看作是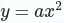的多维扩展表达式，这里我们需要Q为半正定，就是希望Q能起到a≥0的效果，R为正定矩阵就是希望矩阵R能够起到a>0的效果。

          一般的我们认为状态量x为：横向偏差、横向变化率、角度偏差、角度变化率。Q为我们提前标定的对角矩阵，标定值对应以上不同维度的权重，也可以为非对角矩阵，考虑不同维度之间的相互关系。

         控制向量u为：前轮转角、加速度。同样的R也为提前标定的对角矩阵。也可以考虑相互关系。

         Q11选取较大的值，会让x1很快到0；另外一方面，加大R的值，会使得对应的控制量减小，控制器执行更少的动作，意味着系统的状态衰减将变慢。所以要综合看具体的实际应用场景来调节，鱼和熊掌不可兼得。建议在不同场景下采用不同的参数。

3. 公式求解

 假设有一个线性系统能用状态向量的形式表示成：

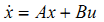
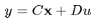
                                                                                                                                                                                                               ( 1 )

其中 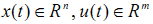，初始条件是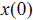. 并且假设这个系统的所有状态变量都是可测量到的。

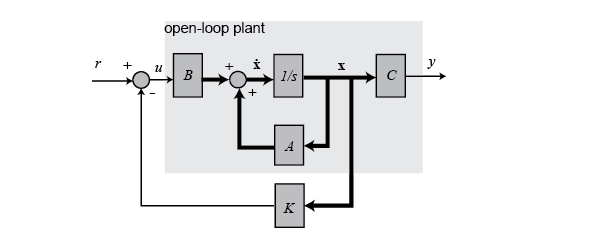
      在介绍LQR前，先简单回顾一下现代控制理论中最基本的控制器--全状态反馈控制。

      全状态反馈控制系统图形如下：

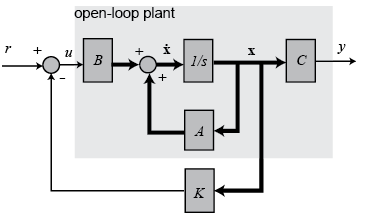
我们要设计一个状态反馈控制器             

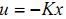
使得闭环系统能够满足我们期望的性能。我们把这种控制代入之前的系统状态方程得到

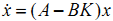
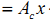
                                            ( 2 )

对于(1)式的开环系统，由现代控制理论我们知道开环传递函数的极点就是系统矩阵A的特征值。(传递函数的分母是|sI -A|，|·|表示行列式)

现在变成了(2)的闭环形式，状态变换矩阵A变成了(A-BK)。因此通过配置反馈矩阵K，可以使得闭环系统的极点达到我们期望的状态。注意，这种控制器的设计与输出矩阵C,D没有关系。

       那么，什么样的极点会使得系统性能很棒呢？并且，当系统变量很多的时候，即使设计好了极点，矩阵K也不好计算。

       于是，LQR为我们设计最优控制器提供了一种思路。

在设计LQR控制器前，我们得设计一个能量函数，最优的控制轨迹应该使得该能量函数最小。一般选取如下形式的能量函数。

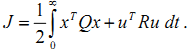            ，其中Q是你自己设计的半正定矩阵，R为正定矩阵。

可是，为什么能量函数(或称系统的目标函数)得设计成这个样子呢？

       首先假设状态向量x(t)是1维的，那么其实就是一个平方项 Qx^2 >= 0，同理. 能量函数J要最小，那么状态向量x(t)，u(t)都得小。J最小，那肯定是个有界的函数，我们能推断当t趋于无穷时，状态向量x(t)将趋于0，这也保证了闭环系统的稳定性。那输入u(t)要小是什么意思呢？它意味着我们用最小的控制代价得到最优的控制。譬如控制电机，输入PWM小，将节省能量。

       再来看看矩阵Q,R的选取，一般来说，Q值选得大意味着，要使得J小，那x(t)需要更小，也就是意味着闭环系统的矩阵(A-BK)的特征值处于S平面左边更远的地方，这样状态x(t)就以更快的速度衰减到0。

另一方面，大的R表示更加关注输入变量u(t),u(t)的减小，意味着状态衰减将变慢。同时，Q为半正定矩阵意味着他的特征值非负，R为正定矩阵意味着它的特征值为正数。如果你选择Q,R都是对角矩阵的话，那么Q的对角元素为正数，允许出现几个0.R的对角元素只能是正数。

       注意LQR调节器是将状态调节到0，这与轨迹跟踪不同，轨迹跟踪是使得系统误差为0.

        知道了背景后，那如何设计反馈矩阵K使得能量函数J最小呢？很多地方都是从最大值原理，Hamilton函数推导出来。这里用另外一种更容易接受的方式推导。

将u = -Kx 代入之前的能量函数得到：

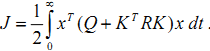                        ( 3 )

为了找到K,我们先不防假设存在一个常量矩阵P使得：

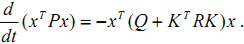                    (4)

代入(3)式得：

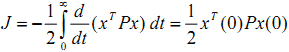                   (5)

注意，我们已经假设闭环系统是稳定的，也就是t趋于无穷时，x(t)趋于0.

现在把(4)式左边的微分展开，并把状态变量x的微分用(2)式替代得到：

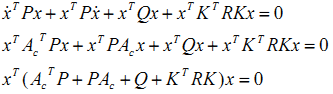
这个式子要始终成立的话，括号里的项必须恒等于0.

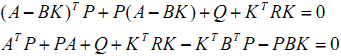
这是一个关于K的二次型等式，当然这个二次型是我们不愿看到的，因为计算复杂。现在只要这个等式成立，我们何必不选择K使得两个二次项正好约掉了呢？这样既符合了要求，又简化了计算。

取 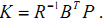   代入上式得：

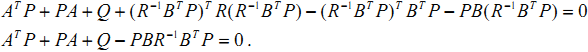             (6)

K的二次项没有了，可K的取值和P有关，而P是我们假设的一个量，P只要使得的(6)式成立就行了。而(6)式在现代控制理论中极其重要，它就是有名的Riccati 方程。

现在回过头总结下LQR控制器是怎么计算反馈矩阵K的：

       1.选择参数矩阵Q,R

       2.求解Riccati 方程得到矩阵P

       3.计算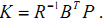

再看看LQR的结构图：

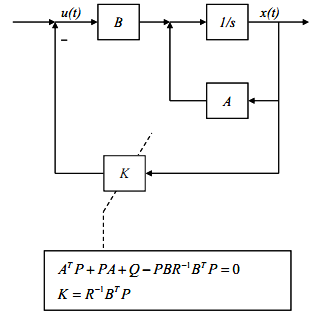
实际应用中，为了消除稳态误差，LQR中还需要加入前馈控制。详细内容可查看：智能驾驶车辆横向控制算法_ChenGuiGan的博客-CSDN博客_自动驾驶横向控制

4. MPC与LQR比较

          首先，LQR的研究对象是现代控制理论中的状态空间方程给出的线性系统，而MPC的研究对象可以是线性系统，也可以是非线性系统。不过现在很多的做法都是将非线性系统线性化，然后进行相关计算，具体要根据自己的工程情况来确定哪种方式比较好，比如之前做MPC的时候，线控车底层速度控制接口就是加速度，那就没必要根据IMU再套嵌个一层PID。

          其次，既然是优化问题，那就离不开目标函数的设计，LQR的目标函数在上面已经有描述，MPC的目标函数，多数都是多个优化目标乘以不同权重然后求和的方式。虽然方式不同，不过都是对达到控制目标的代价累计。

          最后，工作时域上的不同，LQR的计算针对同一工作时域，在一个控制周期内，LQR只计算一次，并将此次计算出的最优解下发给控制器即可；而MPC是滚动优化的，计算未来一段时间内，每个采样周期都会经过计算，得出一组控制序列，但是只将第一个控制值下发给控制器。
————————————————
版权声明：本文为CSDN博主「一实相印」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/zhouyy858/article/details/107606500

最后

以上就是兴奋宝贝为你收集整理的智能驾驶LQR横向控制算法的全部内容，希望文章能够帮你解决智能驾驶LQR横向控制算法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。