1.构建数学模型
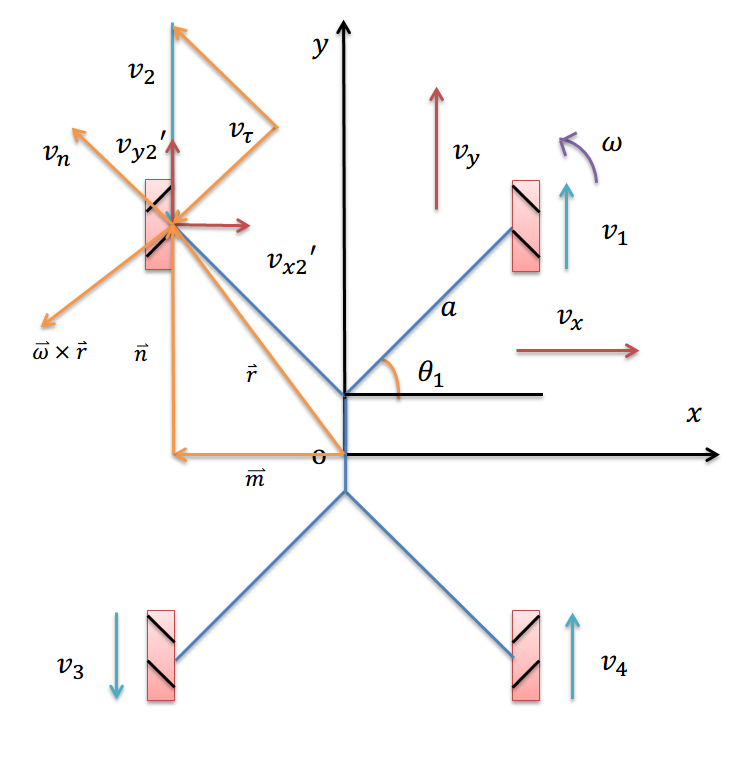
其中
v
i
v_i
vi为轮子的转速,
ω
omega
ω为机器人旋转角速度,
v
x
v_x
vx、
v
y
v_y
vy为本体坐标系中的速度,
r
⃗
i
vec r_i
ri为各轮中心在本体坐标系中的位置矢量,
m
⃗
vec m
m、
n
⃗
vec n
n为位置矢量在
x
x
x、
y
y
y轴上的分量(其大小已知),
θ
i
theta_i
θi为麦轮辊子与
x
x
x轴夹角,
θ
i
=
π
/
4
theta_i=pi/4
θi=π/4。
2.推导速度映射矩阵
设世界坐标系(惯性坐标系)中的机器人速度为 V x V_x Vx、 V y V_y Vy、 W W W, 本体坐标系与世界坐标系的夹角( 即姿态角) 为 α alpha α于是我们可得到:
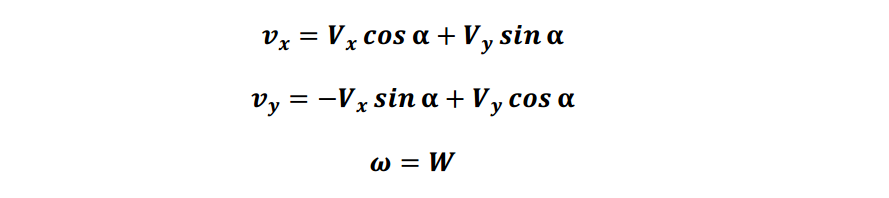 即
即
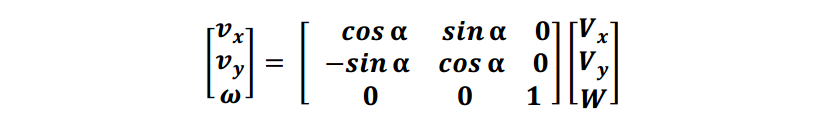
以上即为世界坐标系到本体坐标系的速度映射矩阵, 该矩阵与底盘的轮系没有关系。
3.麦轮速度解算
由于此处旋转中心与轮轴的连线不垂直于棍子,所以使用向量外积对角速度进行处理。
由物理关系
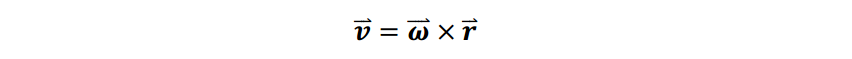
和几何关系
 可得
可得
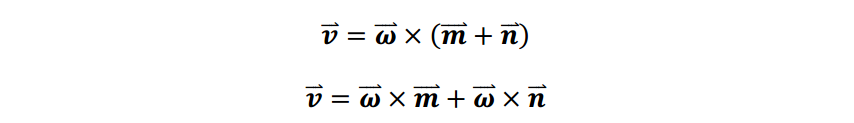
根据上图,将角速度投影到本体坐标轴上,与两轴向速度融合。 可以得到:
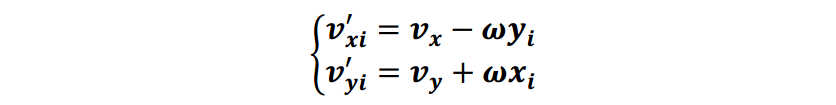
其中
(
x
i
,
y
i
)
( x_i,y_i)
(xi,yi)为各轮轴心位置矢量坐标,分别为
(
m
,
n
)
(m,n)
(m,n),
(
−
m
,
n
)
(-m,n)
(−m,n),
(
−
m
,
−
n
)
(-m,-n)
(−m,−n),
(
m
,
−
n
)
(m,-n)
(m,−n).
如上图轮 2 处所示,褐色箭头
v
x
2
′
v_{x2}^{'}
vx2′、
v
y
2
′
v_{y2}^{'}
vy2′代表将角速度融合到
x
x
x、
y
y
y方向后, 底盘想要的
x
x
x、
y
y
y方向的速度,由于麦轮辊子的速度为从动速度,受底盘其余各轮影响,无法得知其具体值,因此我们将
v
x
2
′
v_{x2}^{'}
vx2′、
v
y
2
′
v_{y2}^{'}
vy2′,分解到垂直辊子方向
v
n
v_n
vn和平行与辊子方向
v
τ
v_tau
vτ,可以得到:
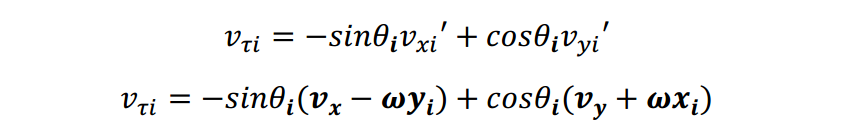
又因为
v
τ
i
v_{tau i}
vτi平行于辊子,因此其速度只可能为电机提供,所以麦轮转速
v
i
v_{ i}
vi为
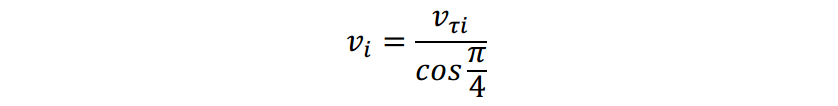
将
θ
i
theta_i
θi、
(
x
i
,
y
i
)
(x_i,y_i)
(xi,yi)带人以上两式, 我们可以得到底盘速度到麦轮速度的转换矩阵
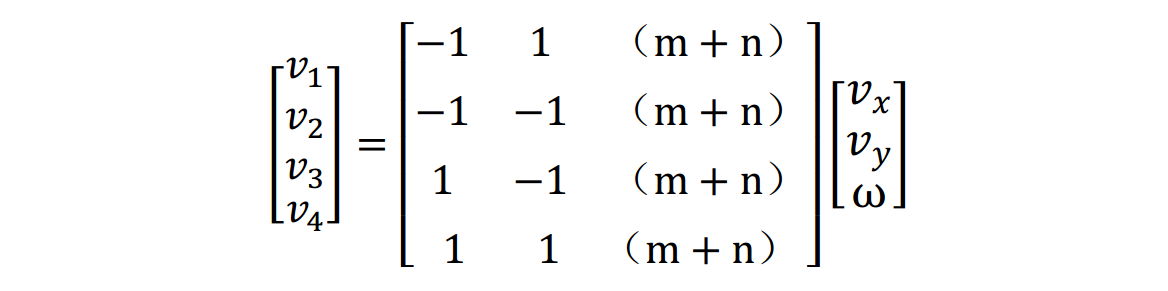
将其与世界坐标系到机身坐标系的转换矩阵相乘可得最终绝对速度到各轮子的转换矩阵
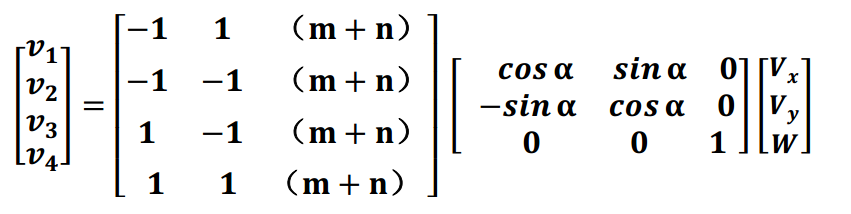
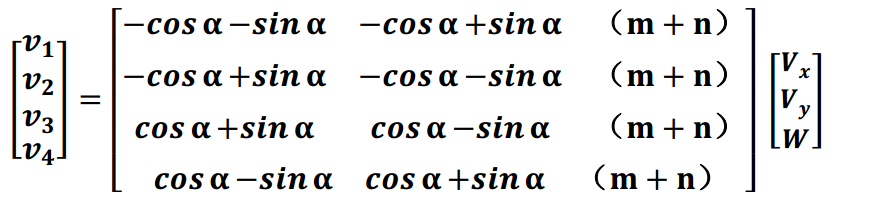
以上即为麦克纳姆轮四轮长方形底盘速度解算。
最后
以上就是天真蓝天最近收集整理的关于麦克纳姆轮四轮长方形底盘速度解算的全部内容,更多相关麦克纳姆轮四轮长方形底盘速度解算内容请搜索靠谱客的其他文章。








发表评论 取消回复