麦克纳姆轮单轮速度分析

  关注同名微信公众号“混沌无形”，阅读更多有趣好文！

原文链接：https://mp.weixin.qq.com/s/GWhlXsuY6QYyoZydaSYpjQ（包含原文PDF百度云下载链接）

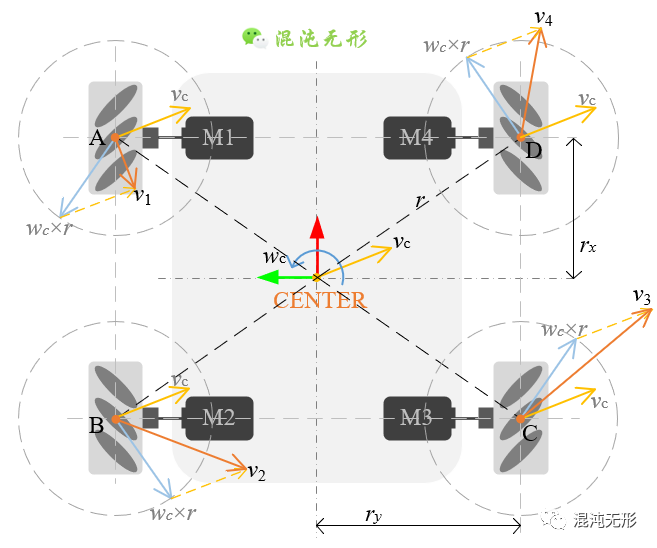
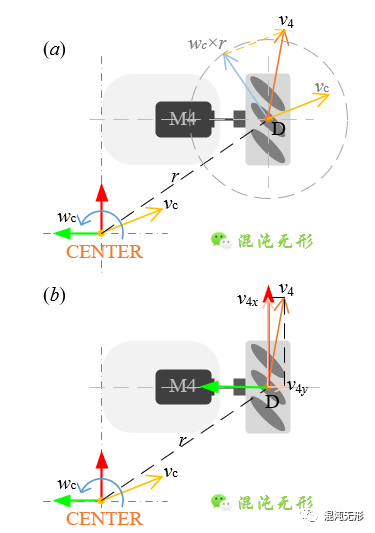
为计算电机输出轴转速，需要进一步分析。这里结合图 2.4和图 2.5（b），先以右前轮为例进行分析，将点D的合速度沿着坐标系xDy分解，表示为

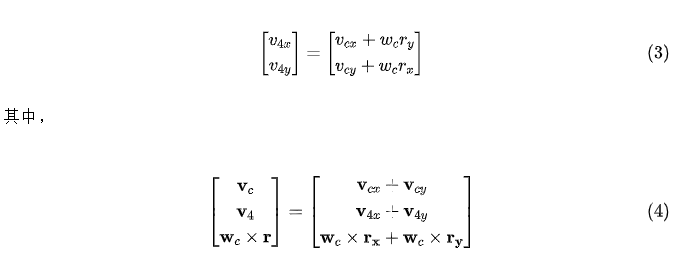
式中，[v4x v4y]T表示v4的在坐标系xDy的分速度，[vcx vcy]T表示vc的分速度，[rx ry]T表示r的在坐标系xDy对应坐标轴下的分量（加粗表示矢量，常规是标量）。 

（对标量的正负号说明：在公式（3）中vcx是正数，vcy是负数，wc为正数（逆时针旋转为正），变量[vcx vcy wc]隐含了符号的，但没有在公式中显示表达出来的原因是我们在实际编程控制时就会输入带符号的形参；但是距离[rx ry]均为正数，也是因为我们习惯将距离表述为正数。变量符号是根据自己建模喜好而定义的，但最好与常规表达一致） 

显然，仅仅按照上述分析，是没法求解电机输出轴转速的。还需要从另外一个角度突破，麦轮是由辊子和轮毂共同组成的，轮毂轴心与电机输出轴固连，电机输出动力让轮毂转动起来，轮毂带动辊子绕轮毂轴线而转动（主动），辊子与地面接触而产生摩擦力而迫使辊子绕辊子轴线转动（被动），所以辊子不仅绕辊子轴线转动，还绕着轮毂轴线而转动，是这两种转动合成了最终的（实际）运动。

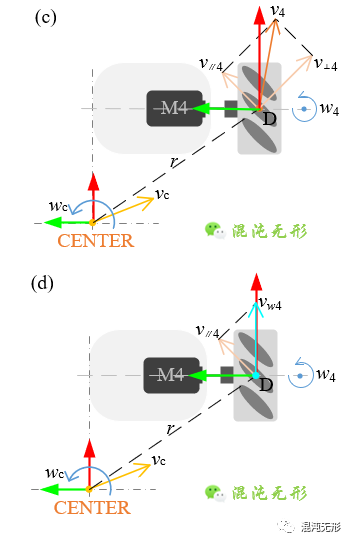
按照上述分析思路，可将右前轮的速度v4沿着辊子轴线方向（v∥4）及辊子滚动方向（v⊥4）进行速度分解，分解效果如图 2.5（c）所示，用数学公式可以表示为

式中，e∥4和e⊥4分别表示平行于辊子轴线及垂直于轴线的单位矢量。 结合公式（3-5），基于坐标系xDy对v∥4进行分析，如下

化简得

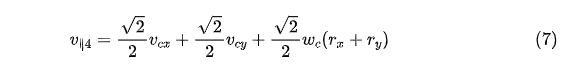
式中，i和j分别表示沿坐标系xDy的坐标轴的单位矢量。 

进一步分析，垂直于辊子轴线的速度（v⊥4）是由辊子被动滚动产生的：①电机轴主动转动带动轮毂转动，轮毂带动辊子运动；②麦轮平台的其他麦轮转动相互影响，由这两种作用力共同产生（关键知识点）。

精彩的理论论证过程见原文链接（含全文下载链接）

由于网页排版效果一般，所以笔者按照期刊论文版式为小伙伴们整理了原文PDF，方便收藏和回味。

原文链接：https://mp.weixin.qq.com/s/GWhlXsuY6QYyoZydaSYpjQ（包含原文PDF百度云下载链接）
CSDN下载链接：https://download.csdn.net/download/qq_19598969/19860792

如果喜欢的话，可以关注同名微信公众号“混沌无形”，阅读更多有趣好文！

最后

以上就是健忘向日葵为你收集整理的麦克纳姆轮单轮速度分析的全部内容，希望文章能够帮你解决麦克纳姆轮单轮速度分析所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。