LQR控制算法及代码实践

背景

假设有一个线性系统能用状态向量的形式表示成：


设计一个状态反馈控制器:
$$u=-Kx$$
则此时状态方程可以写为:

由于让系统稳定的条件是矩阵Acl的特征值的实部均为负数，因此我们可以手动选择几个满足上述条件的特征值，然后反解出K，从而得到控制器。
那么问题来了，我们该如何选择特征值，才能让控制器的控制效果最好呢？现在我们定义一种代价函数:

其中，Q和R是两个对角参数矩阵，Q为半正定矩阵， R为正定矩阵。分别决定了状态向量 x 和输入向量 u 的重要性。显然，J是一个二次型函数，这也是LQR中“Q”的由来。
我们希望的是在满足系统稳定的前提下，通过设计合适的K，让代价函数J最小。
下面我们来分析代价函数的意义。

代价函数的意义

参考这一篇文章：
链接: link
概括来说就是：调节Q的大小可以控制系统状态收敛的快慢；调节R的大小可以控制让系统达到稳态所需输入的大小；

Apollo2.0 LQR控制算法解读

车辆动力学模型的推导可以看这篇：
链接: link

1. 当推导出车辆动力学模型后，选取横向偏差、横向偏差变化率，横摆角角度偏差，横摆角角度偏差变化率作为状态量建立状态空间方程：
   
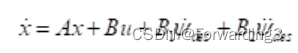
2. 建立目标函数：
   
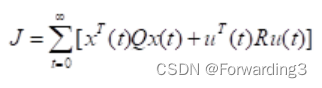
3. 其中Q为状态权重系数，R为控制量权重系数。当上述目标函数最小时就得到最优的状态反馈矩阵K，此时的K可以保证求出最佳控制量，即最佳前轮转角。

4. 上图表示求出最佳转角之后，只能保证（A-BK）x那部分达到稳态，所以还需要增加一个前馈控制量，试另一部分趋近于0.
4. 这个前馈控制量试可以通过纵向车速Vx和道路的半径R计算得到
5. 最终的前轮转角的控制量为最优状态反馈控制量与前馈控制前轮转角之和。计算的出前轮转角经过上下限的限幅后进行输出。
参考链接: link
link

最后

以上就是着急嚓茶为你收集整理的LQR控制算法及代码实践的全部内容，希望文章能够帮你解决LQR控制算法及代码实践所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。