（应用密码学）实验四 流密码

实验四 流密码

线性同余发生器、LFSR及流密码加解密、BBS随机数发生器

• 实验目的

熟悉线性同余发生器算法、BBS随机发生器算法，实现简单的线性反馈移位寄存器（LFSR），理解线性反馈移位寄存器的工作原理，掌握流密码的算法结构和加解密过程。

• 实验要求

• 线性同余发生器

1. 利用线性同余发生器生成伪随机数
2. 分析生成的伪随机数的随机性

• LFSR及流密码加解密

1. 通过不同初始状态生成相应的序列，观察其周期和特点
2. 利用生成的序列对文本进行加解密运算

• BBS随机数发生器

1. 利用BBS随机数发生器生成伪随机数
2. 分析生成的伪随机数的随机性

• 实验原理

• 线性同余发生器

伪随机数序列基于迭代方程：X(n + 1) = (a * X(n) + c) % m

其中, 各系数为:  

                     模m, m > 0

                     系数a, 0 < a < m

                     增量c, 0 <= c < m

                     原始值(种子) 0 <= X(0) < m

其中参数c, m, a比较敏感, 或者说直接影响了伪随机数产生的质量。

• LFSR及流密码加解密

首先我们定义两个线性反馈移位寄存器（LFSR），并对初始状态进行初始化，将LFSR的特征多项式作为密钥由用户输入（我们设置为8位密钥）。得到密钥我们就能根据以下线性反馈移位寄存器（LFSR）的原理，生成两个序列。这个LFSR可以产生的最大序列长度为2^m-1。

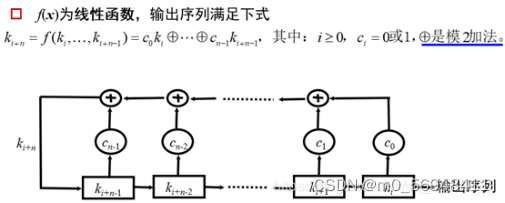
 将两个序列分别作为JK触发器的输入端J、K，并且根据JK触发器的结构及逻辑真值表，可以得到255位的密钥流。

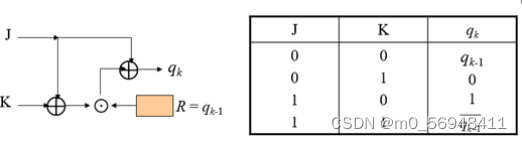
输入明文时，先将明文转换为二进制字符串，进行加密后，再转化为字符串。

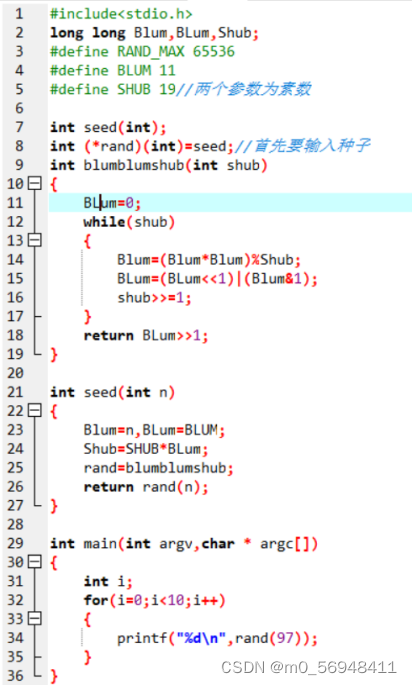
• BBS随机数发生器

BBS算法过程描述如下：

输入：无

输出：生成一个长度为l的伪随机比特序列b1，b2，b3，…，bl。

1. 选择两个大素数p和q作为随机种子，要求它们被4除时都余3，即p    q   

3 mod 4

1. 令n=p*q，选择一个随机数s，使得gcd（s，n）=1。
2. x0=s^2 mod n
3. i从1开始，不断重复以下操作，直到i经过逐次加1后超过l

1. xi=xi-1^2 mod n
2. bi=xi mod 2,即每次迭代都取得xi最低位的比特
3. 输出bi

• 实验内容与步骤

• 线性同余发生器

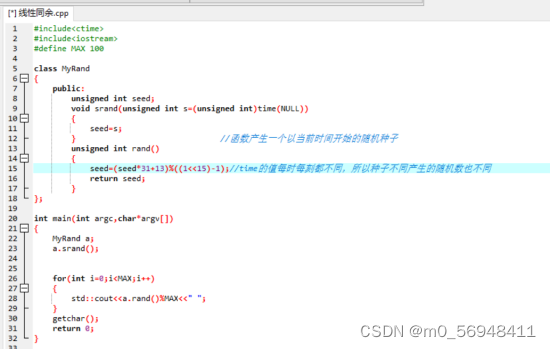
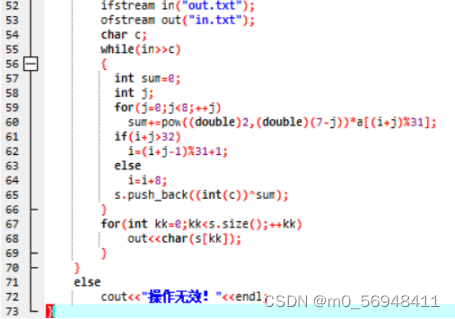
• LFSR及流密码加解密

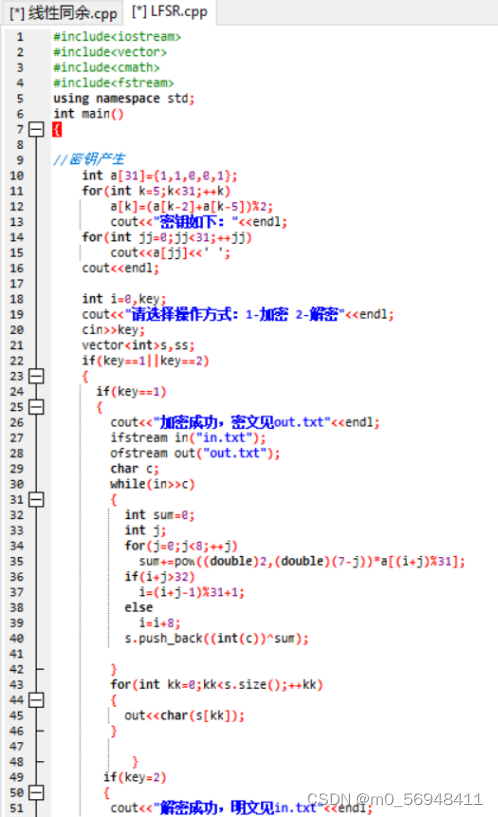
• BBS随机数发生器

• 实验结果

线性同余发生器

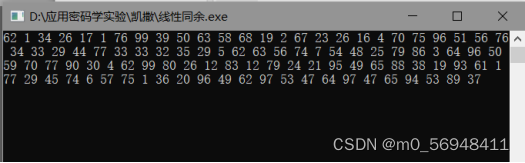
• LFSR及流密码加解密

加密运算：

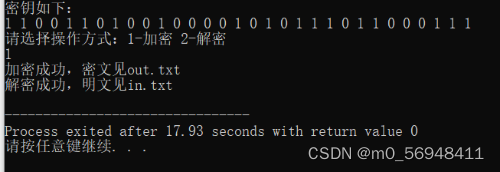
 解密运算：

 BBS随机数发生器

最后

以上就是曾经往事最近收集整理的关于（应用密码学）实验四 流密码的全部内容，更多相关（应用密码学）实验四内容请搜索靠谱客的其他文章。