MATLAB利用FFT对信号进行频谱分析

1.实验目的

(1)进一步加深DFT算法原理和基本性质的理解(因为FFT只是DFT的一种快速算法，所以FFT的运算结果必然满足DFT的基本性质)。

(2)熟悉FFT算法原理和FFT程序的应用。

(3)学习利用FFT对离散时间信号进行频谱分析的方法，了解可能出现的误差及其原因，以便在实际中正确应用FFT。

2.实验原理

用FFT对信号作频分析是学习数字信号处理的重要内容，经常需要进行分析的信号是模拟信号的时域离散信号。对信号进行谱分析的重要问题是频谱分辨率D和分析误差。当N较大时,离散谱的包络才能逼近连续谱，因此N要适当选择大一些。

3.运行结果

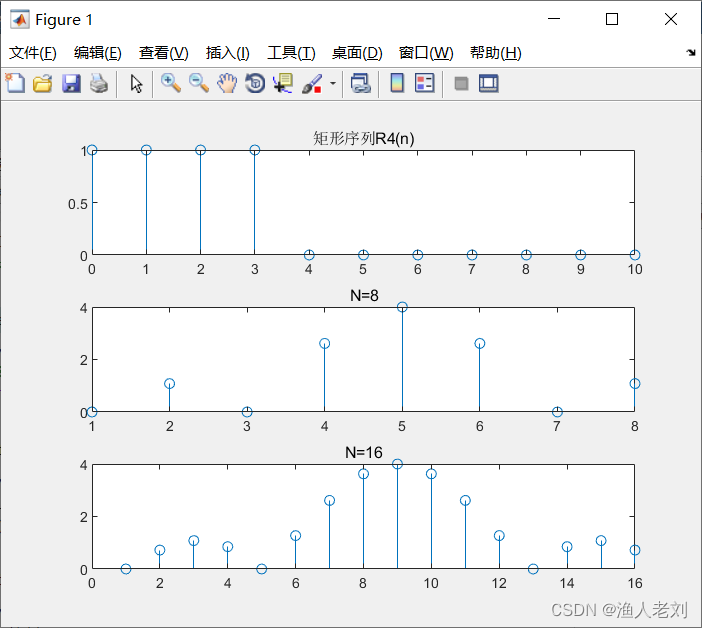图1 x1(n)时域波形及幅频特性曲线

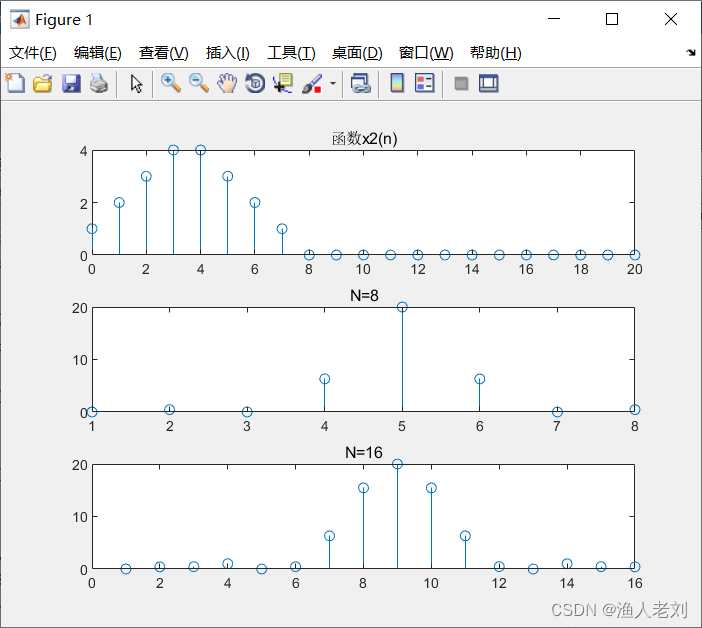图2 x2(n)时域波形及幅频特性曲线

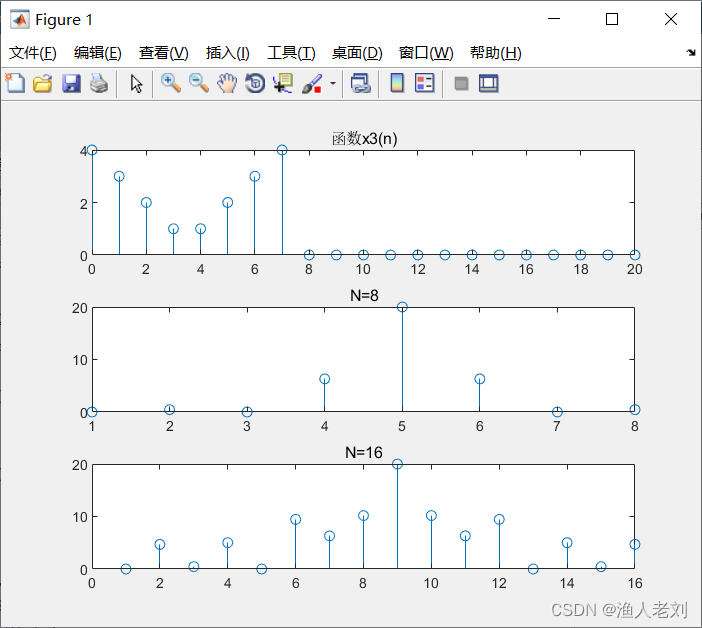图3 x3(n)时域波形及幅频特性曲线

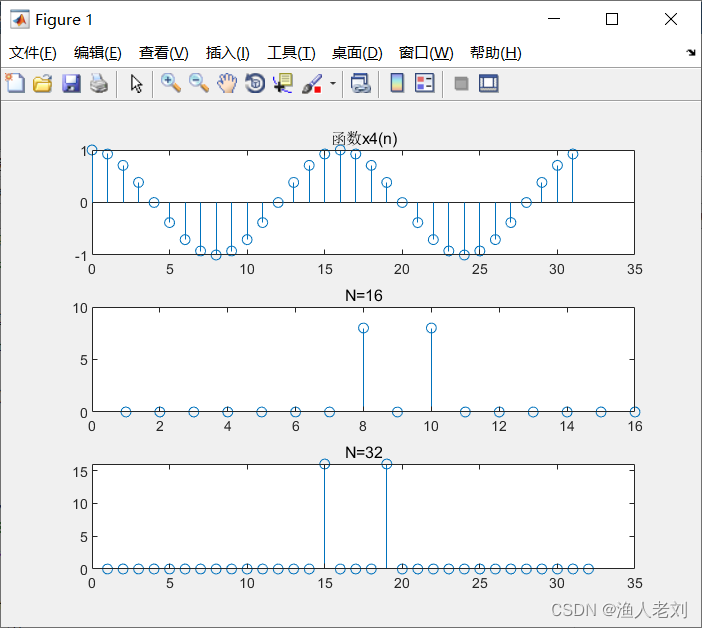图4 x4(n)时域波形及幅频特性曲线

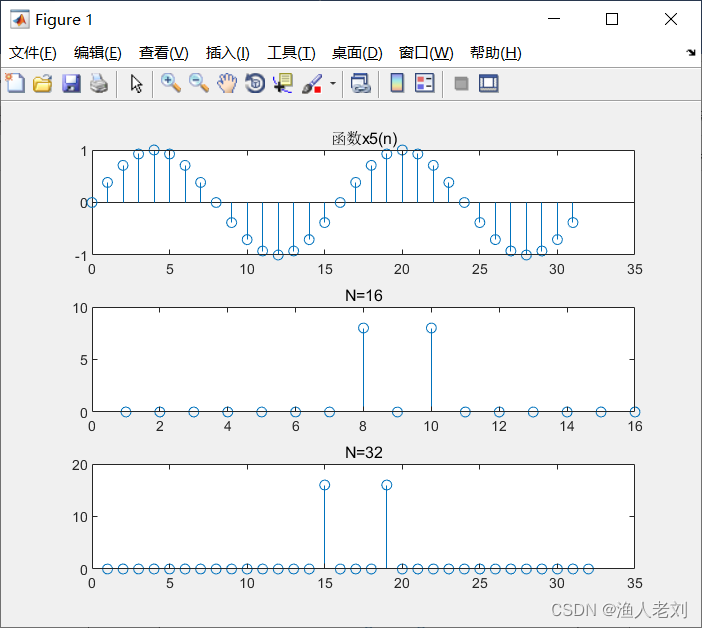图5 x5(n)时域波形及幅频特性曲线

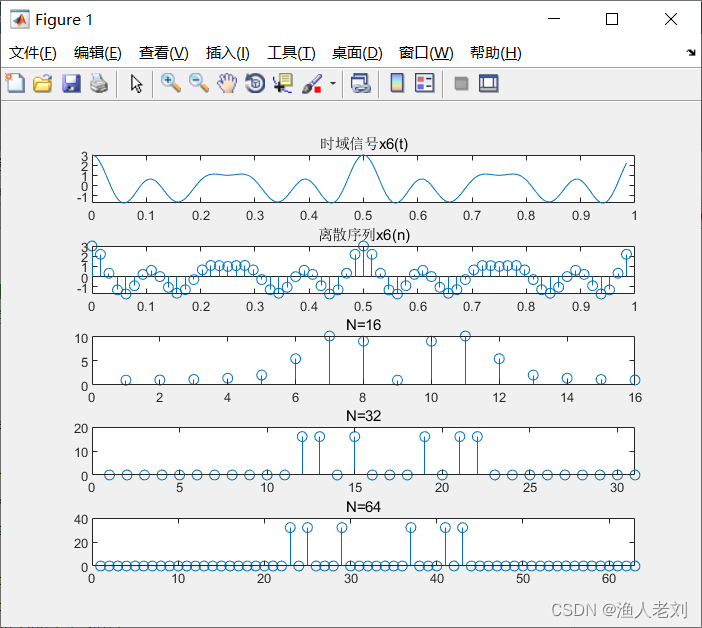图6 x6(n)时域波形及幅频特性曲线

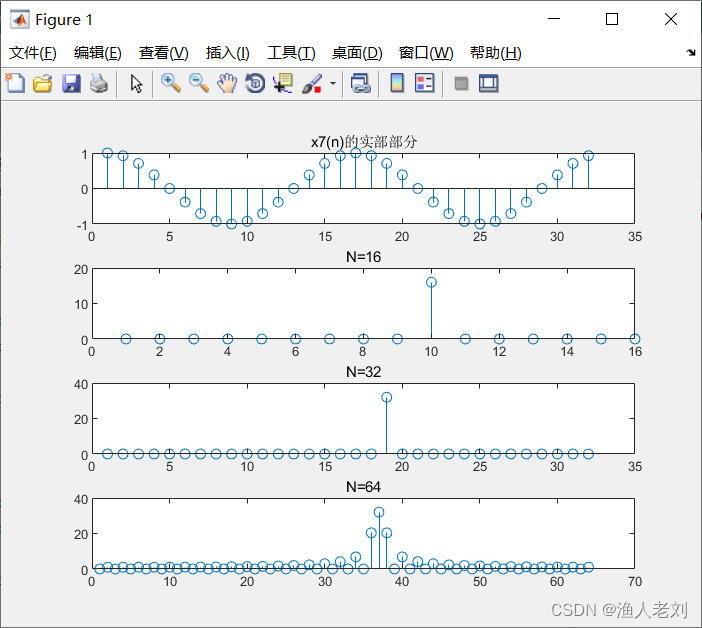
图7 x(n)=x4(n)+jx5(n)时域波形及幅频特性曲线

附：程序代码

(1)

ns=0;

nf=4;

n1=0;

n2=10;

n=[n1:n2];

x=stepseq(ns,n1,n2)-stepseq(nf,n1,n2);

subplot(3,1,1);

stem(n,x);

title('矩形序列R4(n)');

X1_8=fftshift(fft(x,8));

subplot(3,1,2);

stem(abs(X1_8));

title('N=8');

X1_16=fftshift(fft(x,16));

subplot(3,1,3);

stem(abs(X1_16));

title('N=16');

function [x,n]=stepseq(n0,n1,n2)

if n0<n1||n0>n2||n1>n2

    error('参数须满足n1<=n0<=n2');

end

n=[n1:n2];

x=[(n-n0)>=0];

end

(2)

n1=0;

n2=20;

n=[n1:n2];

x=zeros(1,n2-n1+1);

for i=1-n1:n2-n1+1

    if 0<=n(i)&&n(i)<=3

        x(i)=n(i)+1;

    end

    if 4<=n(i)&&n(i)<=7

        x(i)=8-n(i);

    end

end

subplot(3,1,1);

stem(n,x);

title('函数x2(n)');

X8=fftshift(fft(x,8));

subplot(3,1,2);

stem(abs(X8));

title('N=8');

X16=fftshift(fft(x,16));

subplot(3,1,3);

stem(abs(X16));

title('N=16')

(3)

n1=0;

n2=20;

n=[n1:n2];

x=zeros(1,n2-n1+1);

for i=1-n1:n2-n1+1

    if 0<=n(i)&&n(i)<=3

        x(i)=4-n(i);

    end

    if 4<=n(i)&&n(i)<=7

        x(i)=n(i)-3;

    end

end

subplot(3,1,1);

stem(n,x);

title('函数x3(n)');

X8=fftshift(fft(x,8));

subplot(3,1,2);

stem(abs(X8));

title('N=8');

X16=fftshift(fft(x,16));

subplot(3,1,3);

stem(abs(X16));

title('N=16')

(4)

n1=0;

n2=31;

n=[n1:n2];

x=zeros(1,n2-n1+1);µ

for i=1-n1:n2-n1+1

    if 0<=n(i)&&n(i)<=31

        x(i)=cos(pi*n(i)/8);

    end

end

subplot(3,1,1);

stem(n,x);

title('函数x4(n)');

X16=fftshift(fft(x,16));

subplot(3,1,2);

stem(abs(X16));

title('N=16');

X32=fftshift(fft(x,32));

subplot(3,1,3);

stem(abs(X32));

title('N=32')

(5)

n1=0;

n2=31;

n=[n1:n2];

x=zeros(1,n2-n1+1);

for i=1-n1:n2-n1+1

    if 0<=n(i)&&n(i)<=31

        x(i)=sin(pi*n(i)/8);

    end

end

subplot(3,1,1);

stem(n,x);

title('函数x5(n)');

X16=fftshift(fft(x,16));

subplot(3,1,2);

stem(abs(X16));

title('N=16');

X32=fftshift(fft(x,32));

subplot(3,1,3);

stem(abs(X32));

title('N=32')

(6)

fs=64;

N1=16;

N2=32;

N3=64;

delta_t=1/fs;

t=0:delta_t:(N3-1)*delta_t;

t1=0:delta_t/10:(N3-1)*delta_t;

x6=cos(8*pi*t)+cos(16*pi*t)+cos(20*pi*t);

x6_t=cos(8*pi*t1)+cos(16*pi*t1)+cos(20*pi*t1);

x6_1=fftshift(fft(x6,N1));

x6_2=fftshift(fft(x6,N2));

x6_3=fftshift(fft(x6,N3));

subplot(5,1,1);

plot(t1,x6_t);

title('时域信号x6(t)');

subplot(5,1,2);

stem(t,x6);

title('离散序列x6(n)');

subplot(5,1,3);

stem(abs(x6_1));

title('N=16');

subplot(5,1,4);

stem(abs(x6_2));

title('N=32');

axis([0,31,0,20]);

subplot(5,1,5);

stem(abs(x6_3));

title('N=64');

axis([0,63,0,40]);

(7)

n1=0;

n2=31;

n=[n1:n2];

x4=zeros(1,n2-n1+1);

for i=1-n1:n2-n1+1

    if 0<=n(i)&&n(i)<=31

        x4(i)=cos(pi*n(i)/8);

    end

end

x5=zeros(1,n2-n1+1);

for i=1-n1:n2-n1+1

    if 0<=n(i)&&n(i)<=31

        x5(i)=sin(pi*n(i)/8);

    end

end

x7=x4+j*x5;

x7_1=fftshift(fft(x7,16));

x7_2=fftshift(fft(x7,32));

x7_3=fftshift(fft(x7,64));

subplot(4,1,1);

stem(x4);

title('x7(n)的实部部分');

subplot(4,1,2);

stem(abs(x7_1));

title('N=16');

subplot(4,1,3);

stem(abs(x7_2));

title('N=32');

subplot(4,1,4);

stem(abs(x7_3));

title('N=64');

最后

以上就是背后摩托为你收集整理的MATLAB利用FFT对信号进行频谱分析的全部内容，希望文章能够帮你解决MATLAB利用FFT对信号进行频谱分析所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。