窗函数设计FIR滤波器

实验原理????

有限单位冲激响应序列$h(n)$逼近$h_d(n)$；由于$h_d(n)$往往是无限长的序列，且是非因果的，所以用窗函数；

然而截断无限长序列$h_d(n)$来得到有限长序列$h(d)$，可能破坏了序列$h_d(n)$的均匀收敛性，在频谱中波纹幅度响应很大；那么为了减小波纹幅度，可以加大窗的长度N；或使用不同类型的窗函数

常见的窗函数????‍????

矩形窗Boxcar????

$$\begin{gathered} \omega (n)=\{\begin{array}{ll}1& (0\le n\le N-1)\\ 0& (other)\end{array} \\ {W}_R(\omega )=\frac{sin(N\omega /2)}{sin(\omega /2)} \end{gathered}$$

巴特利特窗Bartlett????

也叫三角形窗
$$\begin{gathered} \omega (n)=\{\begin{array}{ll}\frac{2n}{N-1}& (0\le n\le \frac{N-1}{2})\\ 2-\frac{2n}{N-1}& (\frac{N-1}{2}\le n\le N-1)\end{array} \\ W(\omega )=\frac{1}{M}|\frac{sin(N\omega /2)}{sin(\omega /2)}){|}^2(M=\frac{N-1}{2}) \end{gathered}$$

汉宁窗Hanning????

也叫升余弦窗
$$\begin{gathered} \omega (n)=\frac{1}{2}[1-cos(\frac{2n\pi }{N-1})](0\le n\le N-1) \\ or \\ \omega (n)=\frac{1}{2}[1-cos(\frac{2n\pi }{N-1})]{\omega }_R(n) \\ W(e^{jw})=W(w)e^{-jw\alpha } \end{gathered}$$
汉宁窗的频谱幅度:
$$W(\omega )=0.5W_R(\omega )+0.25W_R(\omega -\frac{2\pi }{N-1})+0.25W_R(\omega +\frac{2\pi }{N-1})$$
式中$W_R(\omega )$是矩形窗的频谱幅度函数。这3部分频谱相加使旁瓣抵消，让能量集中在主瓣；代价是使主瓣的宽度翻倍。

哈明窗Hamming????

也叫改进余弦窗
$$\begin{gathered} \omega (n)=[0.54-0.46cos(\frac{2n\pi }{N-1})]{\omega }_R(n) \\ W(\omega )=0.54W_R(\omega )+0.23W_R(\omega -\frac{2\pi }{N-1})+0.23W_R(\omega +\frac{2\pi }{N-1}) \end{gathered}$$

布莱克曼窗Blackman????

$$\begin{gathered} \omega (n)=[0.42-0.5cos(\frac{4n\pi }{N-1})+0.08cos(\frac{4n\pi }{N-1})]{\omega }_R(n) \\ W(\omega )=0.42W_R(\omega )+0.25[W_R(\omega -\frac{2\pi }{N-1})+W_R(\omega +\frac{2\pi }{N-1})] \\ +0.04[W_R(\omega -\frac{4\pi }{N-1})+W_R(\omega +\frac{4\pi }{N-1})] \end{gathered}$$

凯泽窗Kaiser????

$$\omega (n)=\frac{I_0[\beta \sqrt{1-(\frac{2n}{N-1}-1}{)}^2]}{I_0(\beta )}$$

其中$I_0(x)$是第一类修正零阶贝塞尔函数

设计步骤????

1. FIR滤波器的指标：通带截止频率${\omega }_p$；阻带截止频率${\omega }_s$；通带衰减$R_p(db)$；阻带衰减$A_s(db)$。

2. 根据允许的过渡带宽及阻带衰减，初步选择窗函数与N值。

3. 如果是想用理想低通逼近，需求出理想低通的冲激响应$h_d(n)$。

   其理想低通的截止频率应选为：
   $$\begin{gathered} {\omega }_c=\frac{{\omega }_p+{\omega }_s}{2} \\ {h}_d(n)=\frac{1}{2\pi }{\int }_{-{\omega }_c}^{{\omega }_c}{e}^{-jw\alpha }{e}^{jwn}dw \\ =\frac{sin[(n-\alpha ){\omega }_c]}{(n-\alpha )\pi } \end{gathered}$$

4. 将$h_d(n)$与窗函数相乘得FIR滤波器的冲激响应$h(n)$：
   $$h(n)=h_d(n)\omega (n)$$

5. 计算FIR数字滤波器的频率响应，是否达到指标：
   $$H(e^{jw})=\sum _{n=0}^{N-1}h(n)e^{-jwn}$$
   由上式结果计算幅度响应$H(w)$和相位响应$\phi (w)$：
   $$\begin{gathered} H(w)=|H(e^{jw})| \\ \phi (w)=arg[H(e^{jw})] \end{gathered}$$

MATLAB实现????

技术指标：

• 通带截止频率：${\omega }_p=0.2\pi$；阻带截止频率：${\omega }_p=0.3\pi$
• 通带衰减：$R_p=0.35db$；阻带衰减：$R_p=30db$

%理想低通滤波器的计算
function hd = idea_lowfilter(wc,num)
    a = (num-1)/2;
    n = [0:1:(num-1)];
    delta = n-a+eps;
    hd = sin(wc*delta)./(pi*delta);
end

clear;clc;
%指标
wp = 0.2*pi; ws = 0.3*pi;
N = 51;
n = [0:1:N-1];
%理想低通截止频率
wc = (wp+ws)/2;
%理想低通的冲激响应
hd = idea_lowfilter(wc,N);
%FIR滤波器的冲激响应
%矩形窗：h1；汉宁窗：h2；哈明窗：h3；凯泽窗：h4
w_box = boxcar(N)';
w_han = hann(N)';
w_ham = hamming(N)';
w_kaiser = kaiser(N)';
h1 = hd.*w_box;
h2 = hd.*w_han;
h3 = hd.*w_ham;
h4 = hd.*w_kaiser;
%计算频率响应
[H1,w1]=freqz(h1,1);
[H2,w2]=freqz(h2,1);
[H3,w3]=freqz(h3,1);
[H4,w4]=freqz(h4,1);
%plot
figure
stem(n,hd);title('理想冲激响应');

filplot(n,w1,h1,w_box,H1,'矩形窗');
filplot(n,w2,h2,w_han,H2,'汉宁窗');
filplot(n,w3,h3,w_ham,H3,'哈明窗');
filplot(n,w4,h4,w_kaiser,H4,'凯泽窗');

%plot
function filplot(n,w,response,win,frequency,type)
    figure
    subplot(2,2,1);stem(n,response);title('实际冲激响应');
    subplot(2,2,2);stem(n,win);title(type);
    subplot(2,2,3);plot(w/pi,20*log10(abs(frequency)));title('幅度响应');
    subplot(2,2,4);plot(w/pi,angle(frequency));title('相位响应');
end
    

结果在这里????：

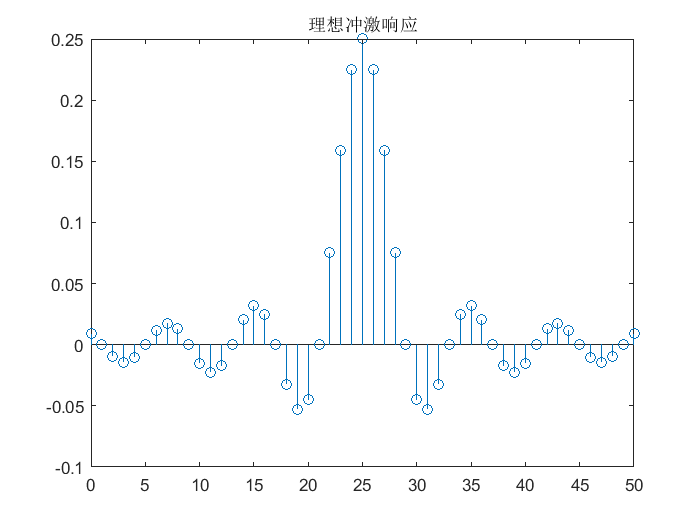
• boxcar

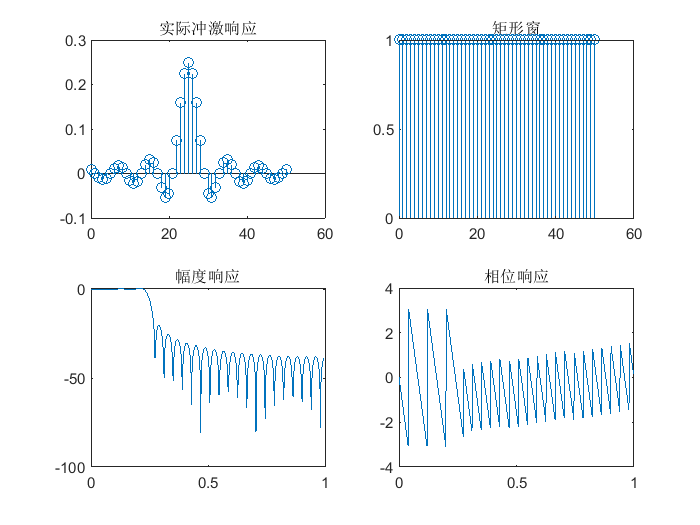
• hanning

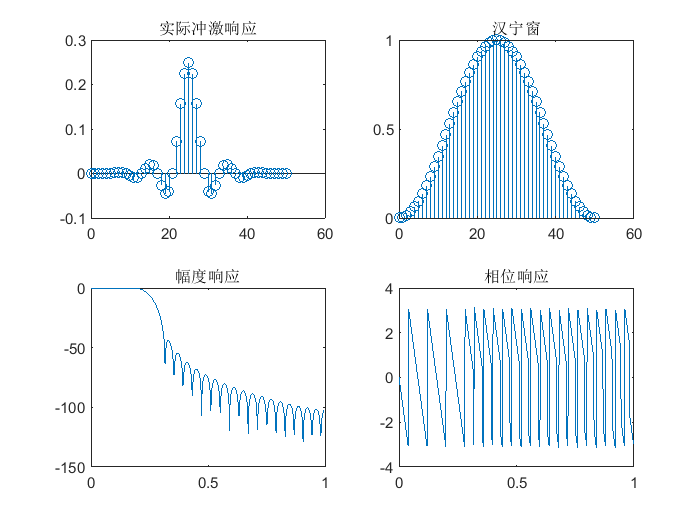
• hamming
  

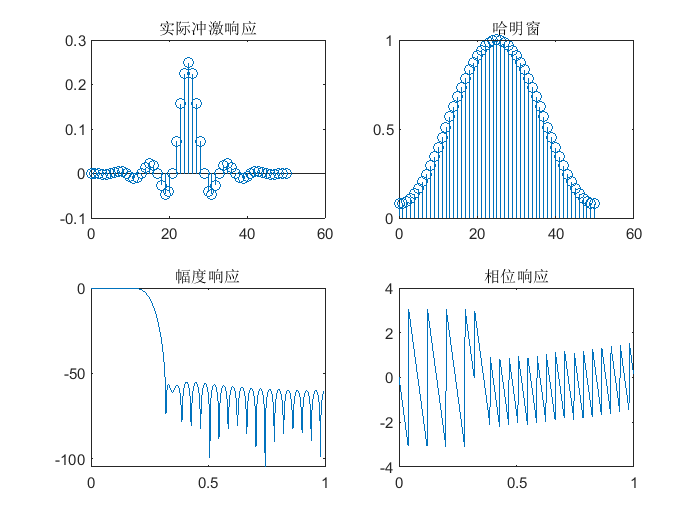
• kaizer

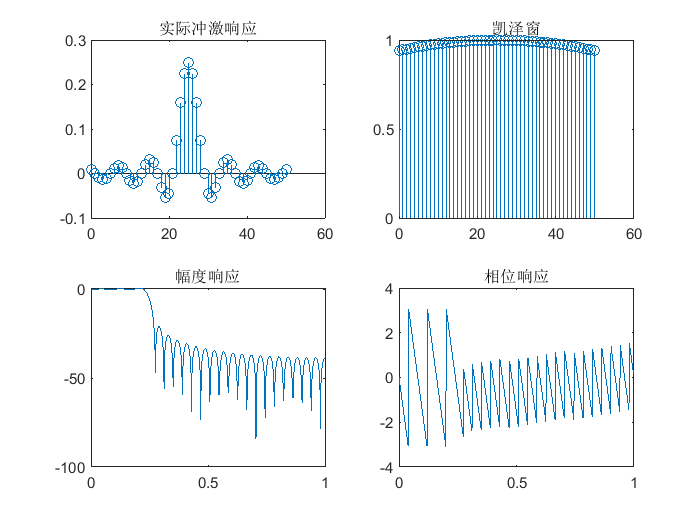
• 窗函数N取值对幅度响应的影响

1. N=61

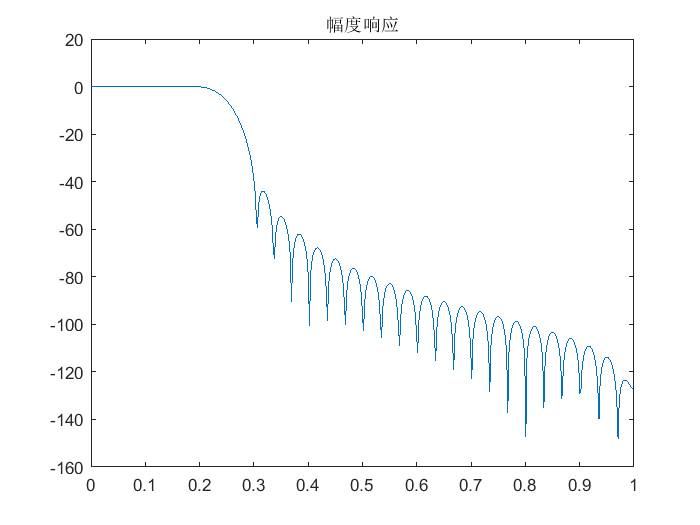
2. N=81

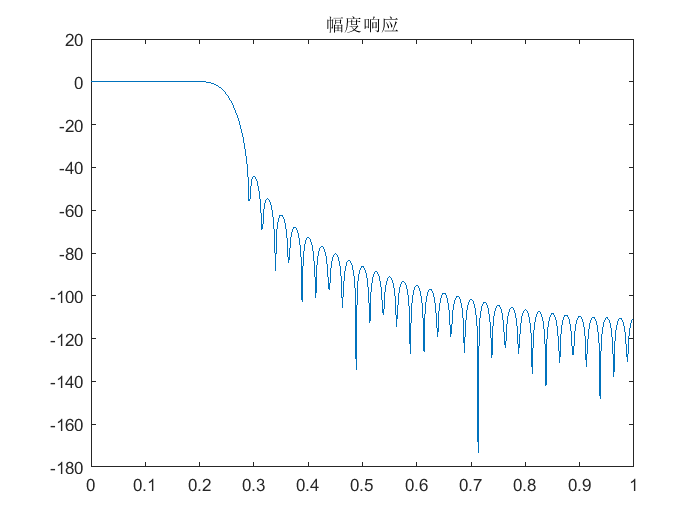
• 窗函数法设计FIR滤波器的主要特点

窗函数设计FIR滤波器是从时域进行设计的。理想低通滤波器加窗处理后，主要受两方面影响。

1. ????滤波器的频率响应在不连续点出现过渡带，过渡带的宽度取决于窗函数主瓣的宽度，一般过渡带宽度与N成反比
2. ????滤波器在通带和主带产生波纹，主要是窗函数的频谱的旁瓣造成；旁瓣的高度要尽可能小，让能量集中在主瓣，减小通带和阻带之间的波纹；主瓣宽度尽可能窄，以获得尽可能陡的过渡带，即N要大。但是这两点又是互相矛盾的：降低旁瓣高度那么主瓣会变宽，让主瓣变窄那么旁瓣会变高。

所以可以采用不同类型的窗函数来改善不均匀收敛性

????????????看到这里了不如整个关注，留点精彩评论吧????????????

最后

以上就是英俊帽子为你收集整理的窗函数设计FIR滤波器的全部内容，希望文章能够帮你解决窗函数设计FIR滤波器所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。