fft

快速傅里叶变换

语法

Y = fft(X)

Y = fft(X,n)

Y = fft(X,n,dim)

说明

示例

Y = fft(X) 用快速傅里叶变换 (FFT) 算法计算 X 的离散傅里叶变换 (DFT)。

• 如果 X 是向量，则 fft(X) 返回该向量的傅里叶变换。

• 如果 X 是矩阵，则 fft(X) 将 X 的各列视为向量，并返回每列的傅里叶变换。

• 如果 X 是一个多维数组，则 fft(X) 将沿大小不等于 1 的第一个数组维度的值视为向量，并返回每个向量的傅里叶变换。

示例

Y = fft(X,n) 返回 n 点 DFT。如果未指定任何值，则 Y 的大小与 X 相同。

• 如果 X 是向量且 X 的长度小于 n，则为 X 补上尾零以达到长度 n。

• 如果 X 是向量且 X 的长度大于 n，则对 X 进行截断以达到长度 n。

• 如果 X 是矩阵，则每列的处理与在向量情况下相同。

• 如果 X 为多维数组，则大小不等于 1 的第一个数组维度的处理与在向量情况下相同。

示例

Y = fft(X,n,dim) 返回沿维度 dim 的傅里叶变换。例如，如果 X 是矩阵，则 fft(X,n,2) 返回每行的 n 点傅里叶变换。

示例

全部折叠

噪声信号

Try This Example 

使用傅里叶变换求噪声中隐藏的信号的频率分量。

指定信号的参数，采样频率为 1 kHz，信号持续时间为 1.5 秒。

Fs = 1000;            % Sampling frequency                    
T = 1/Fs;             % Sampling period       
L = 1500;             % Length of signal
t = (0:L-1)*T;        % Time vector

构造一个信号，其中包含幅值为 0.7 的 50 Hz 正弦量和幅值为 1 的 120 Hz 正弦量。

S = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t);

用均值为零、方差为 4 的白噪声扰乱该信号。

X = S + 2*randn(size(t));

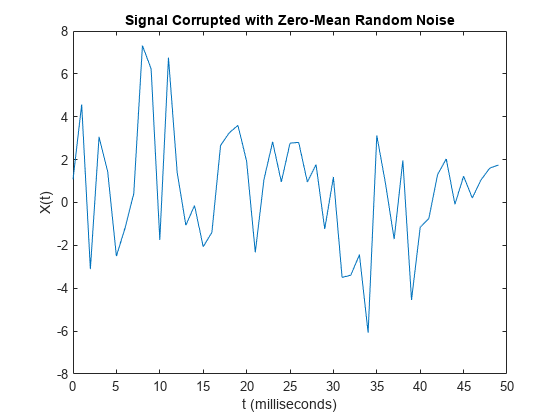
在时域中绘制噪声信号。通过查看信号 X(t) 很难确定频率分量。

plot(1000*t(1:50),X(1:50))
title('Signal Corrupted with Zero-Mean Random Noise')
xlabel('t (milliseconds)')
ylabel('X(t)')

计算信号的傅里叶变换。

Y = fft(X);

计算双侧频谱 P2。然后基于 P2 和偶数信号长度 L 计算单侧频谱 P1。

P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);

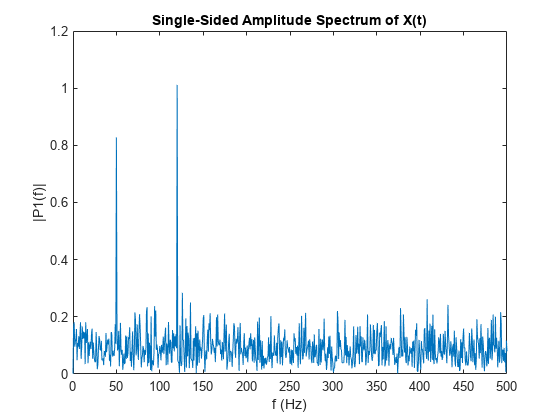
定义频域 f 并绘制单侧幅值频谱 P1。与预期相符，由于增加了噪声，幅值并不精确等于 0.7 和 1。一般情况下，较长的信号会产生更好的频率近似值。

f = Fs*(0:(L/2))/L;
plot(f,P1) 
title('Single-Sided Amplitude Spectrum of X(t)')
xlabel('f (Hz)')
ylabel('|P1(f)|')

现在，采用原始的、未破坏信号的傅里叶变换并检索精确幅值 0.7 和 1.0。

Y = fft(S);
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);

plot(f,P1) 
title('Single-Sided Amplitude Spectrum of S(t)')
xlabel('f (Hz)')
ylabel('|P1(f)|')

高斯脉冲

Try This Example 

将高斯脉冲从时域转换为频域。

定义信号参数和高斯脉冲 X。

Fs = 100;           % Sampling frequency
t = -0.5:1/Fs:0.5;  % Time vector 
L = length(t);      % Signal length

X = 1/(4*sqrt(2*pi*0.01))*(exp(-t.^2/(2*0.01)));

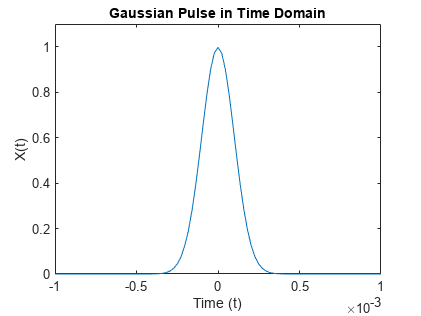
在时域中绘制脉冲。

plot(t,X)
title('Gaussian Pulse in Time Domain')
xlabel('Time (t)')
ylabel('X(t)')

要使用 fft 将信号转换为频域，首先从原始信号长度确定是下一个 2 次幂的新输入长度。这将用尾随零填充信号 X 以改善 fft 的性能。

n = 2^nextpow2(L);

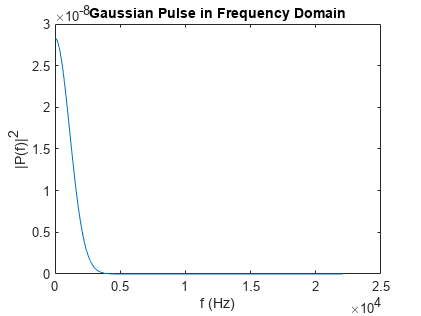
将高斯脉冲转换为频域。

Y = fft(X,n);

定义频域并绘制唯一频率。

f = Fs*(0:(n/2))/n;
P = abs(Y/n);

plot(f,P(1:n/2+1)) 
title('Gaussian Pulse in Frequency Domain')
xlabel('Frequency (f)')
ylabel('|P(f)|')

余弦波

Try This Example 

比较时域和频域中的余弦波。

指定信号的参数，采样频率为 1kHz，信号持续时间为 1 秒。

Fs = 1000;                    % Sampling frequency
T = 1/Fs;                     % Sampling period
L = 1000;                     % Length of signal
t = (0:L-1)*T;                % Time vector

创建一个矩阵，其中每一行代表一个频率经过缩放的余弦波。结果 X 为 3×1000 矩阵。第一行的波频为 50，第二行的波频为 150，第三行的波频为 300。

x1 = cos(2*pi*50*t);          % First row wave
x2 = cos(2*pi*150*t);         % Second row wave
x3 = cos(2*pi*300*t);         % Third row wave

X = [x1; x2; x3];

在单个图窗中按顺序绘制 X 的每行的前 100 个条目，并比较其频率。

for i = 1:3
    subplot(3,1,i)
    plot(t(1:100),X(i,1:100))
    title(['Row ',num2str(i),' in the Time Domain'])
end

出于算法性能的考虑，fft 允许您用尾随零填充输入。在这种情况下，用零填充 X 的每一行，以使每行的长度为比当前长度大的下一个最小的 2 的次幂值。使用 nextpow2 函数定义新长度。

n = 2^nextpow2(L);

指定 dim 参数沿 X 的行（即对每个信号）使用 fft。

dim = 2;

计算信号的傅里叶变换。

Y = fft(X,n,dim);

计算每个信号的双侧频谱和单侧频谱。

P2 = abs(Y/L);
P1 = P2(:,1:n/2+1);
P1(:,2:end-1) = 2*P1(:,2:end-1);

在频域内，为单个图窗中的每一行绘制单侧幅值频谱。

for i=1:3
    subplot(3,1,i)
    plot(0:(Fs/n):(Fs/2-Fs/n),P1(i,1:n/2))
    title(['Row ',num2str(i),' in the Frequency Domain'])
end

输入参数

全部折叠

X - 输入数组
向量 | 矩阵 | 多维数组

输入数组，指定为向量、矩阵或多维数组。

如果 X 为 0×0 空矩阵，则 fft(X) 返回一个 0×0 空矩阵。

数据类型： double | single | int8 | int16 | int32 | uint8 | uint16 | uint32 | logical
复数支持： 是

n - 变换长度
[] （默认） | 非负整数标量

变换长度，指定为 [] 或非负整数标量。为变换长度指定正整数标量可以提高 fft 的性能。通常，长度指定为 2 的幂或可分解为小质数的乘积的值。如果 n 小于信号的长度，则 fft 忽略第 n 个条目之后的剩余信号值，并返回截断的结果。如果 n 为 0，则 fft 返回空矩阵。

示例： n = 2^nextpow2(size(X,1))

数据类型： double | single | int8 | int16 | int32 | uint8 | uint16 | uint32 | logical

dim - 沿其运算的维度
正整数标量

沿其运算的维度，指定为正整数标量。如果未指定值，则默认值是大小不等于 1 的第一个数组维度。

• fft(X,[],1) 沿 X 的各列进行运算，并返回每列的傅里叶变换。

  

• fft(X,[],2) 沿 X 的各行进行运算，并返回每行的傅里叶变换。

  

如果 dim 大于 ndims(X)，则 fft(X,[],dim) 返回 X。当指定 n 时，fft(X,n,dim) 将对 X 进行填充或截断，以使维度 dim 的长度为 n。

数据类型： double | single | int8 | int16 | int32 | uint8 | uint16 | uint32 | logical

输出参数

全部折叠

Y - 频域表示
向量 | 矩阵 | 多维数组

频域表示，以向量、矩阵或多维数组形式返回。

如果 X 的类型为 single，则 fft 本身以单精度进行计算，Y 的类型也是 single。否则，Y 以 double 类型返回。

Y 的大小如下：

• 对于 Y = fft(X) 或 Y = fft(X,[],dim)，Y 的大小等于 X 的大小。

• 对于 Y = fft(X,n,dim)，size(Y,dim) 的值等于 n，而所有其他维度的大小保持与在 X 中相同。

如果 X 为实数，则 Y 是共轭对称的，且 Y 中特征点的数量为 ceil((n+1)/2)。

数据类型： double | single

详细信息

向量的离散傅里叶变换

Y = fft(X) 和 X = ifft(Y) 分别实现傅里叶变换和逆傅里叶变换。对于长度 n 的 X 和 Y，这些变换定义如下：

Y(k)=nj=1X(j) W(j−1)​(k−1)nX(j)=1nnk=1Y(k) Wn−(j−1)​(k−1),

其中

Wn=e(−2πi)/n

为 n 次单位根之一。

提示

• fft 的执行时间取决于变换的长度。仅具有小质因数的变换长度的 fft 执行时间明显快于本身是质数或具有较大质因数的变换长度的 fft 执行时间。

• 对于大多数 n 值，实数输入的 DFT 需要的计算时间大致是复数输入的 DFT 计算时间的一半。但是，当 n 有较大的质因数时，速度很少有差别或没有差别。

• 使用工具函数 fftw 可能会提高 fft 的速度。此函数控制用于计算特殊大小和维度的 FFT 算法优化。

算法

FFT 函数（fft、fft2、fftn、ifft、ifft2、ifftn）基于一个称为 FFTW [1] [2] 的库。

参考

[1] FFTW (http://www.fftw.org)

[2] Frigo, M., and S. G. Johnson. “FFTW: An Adaptive Software Architecture for the FFT.” Proceedings of the International Conference on Acoustics, Speech, and Signal Processing. Vol. 3, 1998, pp. 1381-1384.

另请参阅

fft2 | fftn | fftshift | fftw | ifft

主题

• 傅里叶变换

最后

以上就是谨慎睫毛最近收集整理的关于FFT详解fft的全部内容，更多相关FFT详解fft内容请搜索靠谱客的其他文章。