计算机图形与OpenGL学习五(二维几何变换1.平移、旋转、缩放)

84 阅读 0 评论 56 点赞

我是靠谱客的博主碧蓝日记本，最近开发中收集的这篇文章主要介绍计算机图形与OpenGL学习五(二维几何变换1.平移、旋转、缩放)，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

二维几何变换（平移、旋转、缩放）

本章涉及数学变换比较多，代码是次要的，数学理论可自己推导一下。

【二维平移】

通过将二维量加到一个点的坐标上来生成一个新的坐标位置，可以实现一次平移。将平移距离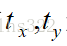加到原始坐标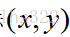上获得一个新的坐标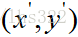,实现一个二维位置的平移。

为平移向量，使用列向量来表示各点坐标的话：

实例：

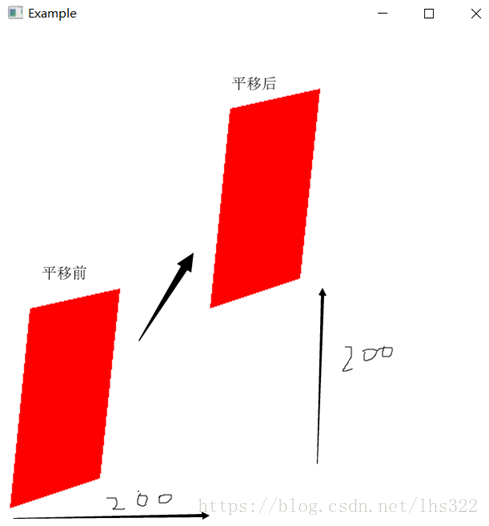
对一个四边形进行平移，平移量自己输入，结果图平移量为(200，200)，代码：

#include<GL/glut.h>
#include<math.h>
#include<Windows.h>
#include<iostream>
#include<stdlib.h>
using namespace std;
GLsizei winWidth = 500, winHeight = 500;
GLuint regHex;//显示表标识
class wcPt2D
{
public:
	GLfloat x, y;
	wcPt2D(GLfloat x=0,GLfloat y=0)
	{
		this->x = x;
		this->y = y;
	}
};
wcPt2D verts[4] = { wcPt2D(10.0, 20.0), wcPt2D(100.0, 50.0), wcPt2D(120, 240.0), wcPt2D (30.0,220.0)};
GLfloat tx; GLfloat ty;
void Move(wcPt2D *verts,GLfloat tx,GLfloat ty)
{
	//平移函数，作为例子平移四边形
	GLint nverts = 4;
	GLint k;
	wcPt2D newVerts[4];//使用一个新的顶点对象集，方便观察平移效果
	for (k = 0; k < nverts;++k)
	{
		newVerts[k].x = verts[k].x + tx;
		newVerts[k].y = verts[k].y + ty;
	}
	
	glBegin(GL_QUADS);
	for (k = 0; k < nverts; ++k)
	{
		glVertex2f(verts[k].x, verts[k].y);
	}
	for (k = 0; k < nverts; ++k)
	{
		glVertex2f(newVerts[k].x, newVerts[k].y);
	}
	glEnd();

	glFlush();
}
void funcPlot()
{
	glClear(GL_COLOR_BUFFER_BIT);
	Move(verts,tx,ty);
}

static void init(void)
{
	//初始化函数，并加入表

	glClearColor(1.0, 1.0, 1.0, 0.0);//设置为白色背景
	regHex = glGenLists(1);//获得一个标识
	glColor3f(1.0, 0.0,0.0);
	glPointSize(2);
	

}



void winReshapeFcn(int newWidth, int newHeight)
{
	//窗口重定形函数
	glMatrixMode(GL_PROJECTION);
	glLoadIdentity();//将当前的用户坐标系的原点移到了屏幕中心：类似于一个复位操作
	gluOrtho2D(0.0, (GLdouble)newWidth, 0.0, (GLdouble)newWidth);
	glClear(GL_COLOR_BUFFER_BIT);


} int main(int argc, char**argv)
{
	glutInit(&argc, argv);
	glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
	glutInitWindowPosition(100, 100);
	glutInitWindowSize(winWidth, winHeight);
	glutCreateWindow("Example");
	cout << "输入x,y偏移量（范围为0-200,0-200)：" << endl;
	cin >> tx >> ty;
	init();
	glutDisplayFunc(funcPlot);
	glutReshapeFunc(winReshapeFcn);
	glutMainLoop();
	return 0;
}

结果：

【二维旋转】

通过指定一个旋转轴和一个旋转角度，进行一次旋转，即是让对象的所有顶点按指定角度绕指定旋转轴旋转。

当绕原点旋转时，设是点的原始角度位置与水平线的夹角，是旋转角。旋转后的坐标表示为：

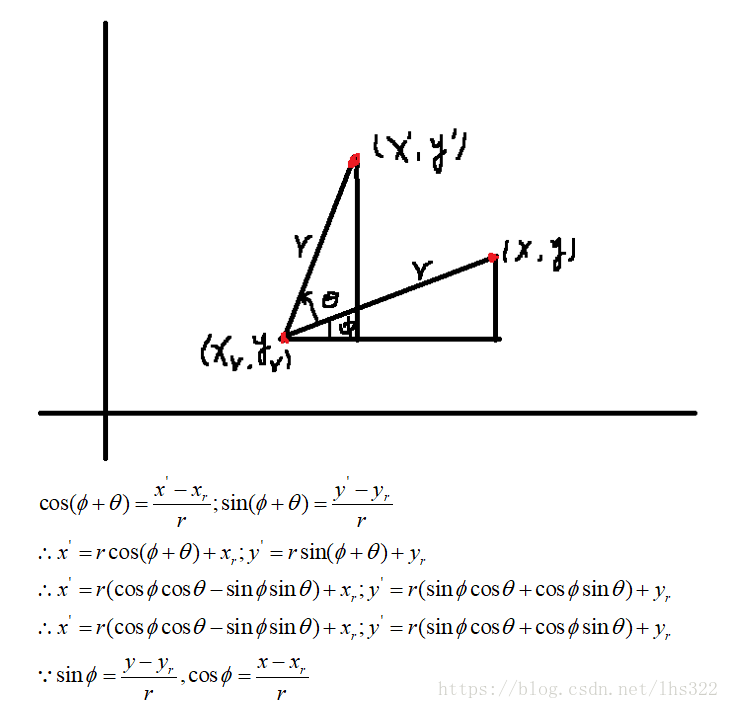
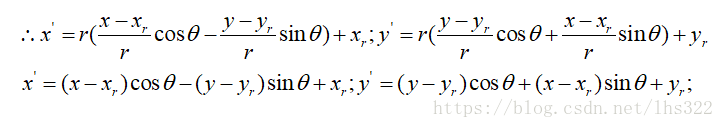
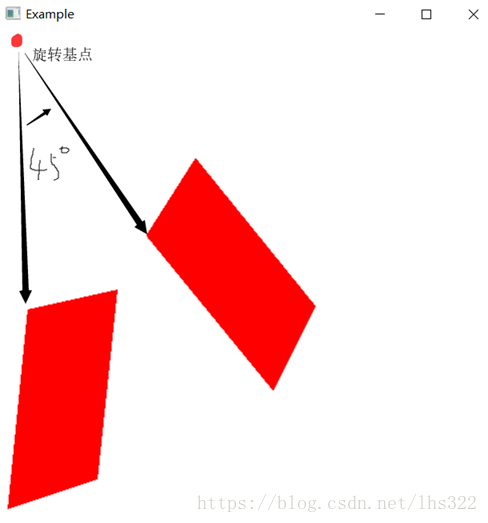
实例：将上个例子的四边形，输入旋转基点，绕指定角度。本次结果为基点(0,450)，旋转角度45°。代码与平移相似，只展示核心代码：

class wcPt2D
{
public:
	GLfloat x, y;
	wcPt2D(GLfloat x=0,GLfloat y=0)
	{
		this->x = x;
		this->y = y;
	}
};
wcPt2D verts[4] = { wcPt2D(10.0, 20.0), wcPt2D(100.0, 50.0), wcPt2D(120, 240.0), wcPt2D (30.0,220.0)};
GLfloat xr; GLfloat yr;//基准点
GLdouble theta;//旋转角度
void rotate(wcPt2D *verts,GLfloat xr,GLfloat yr,GLdouble theta)
{
	//旋转函数，作为例子平移四边形
	GLint nverts = 4;
	GLint k;
	wcPt2D newVerts[4];//使用一个新的顶点对象集，方便观察平移效果
	for (k = 0; k < nverts;++k)
	{
		newVerts[k].x = xr + (verts[k].x - xr)*cos(theta) - (verts[k].y - yr)*sin(theta);
		newVerts[k].y = yr + (verts[k].x - xr)*sin(theta) + (verts[k].y - yr)*cos(theta);
	}
	
	glBegin(GL_QUADS);
	for (k = 0; k < nverts; ++k)
	{
		glVertex2f(verts[k].x, verts[k].y);
	}
	for (k = 0; k < nverts; ++k)
	{
		glVertex2f(newVerts[k].x, newVerts[k].y);
	}
	glEnd();

	glFlush();
}

结果：

【二维缩放】

改变一个对象的大小，可使用缩放变换。一个简单的二维缩放操作可通过将缩放系数和与对象坐标位置相乘得到：

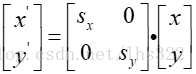
当缩放系数绝对值小于1时，缩放对象向原点靠近；当缩放系数绝对值大于1时，缩放对象远离原点。我们可以选择一个在缩放后不改变位置的点，称为固定点。固定点设为(xf,yf)，缩放后的坐标可计算为：

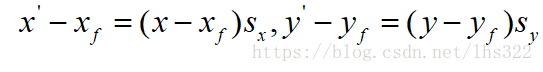
等式变形为：

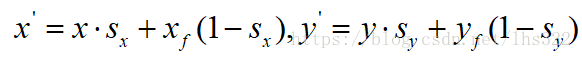
实例：

依然用上面的四边形，选择左下角的点作为缩放基点，缩放系数需要输入，结果是缩放系数Sx,Sy=2时的效果。缩放后我进行了200像素的向左平移，以获得对比效果，核心代码如下：

class wcPt2D
{
public:
	GLfloat x, y;
	wcPt2D(GLfloat x=0,GLfloat y=0)
	{
		this->x = x;
		this->y = y;
	}
};
wcPt2D verts[4] = { wcPt2D(10.0, 20.0), wcPt2D(100.0, 50.0), wcPt2D(120, 240.0), wcPt2D (30.0,220.0)};
GLfloat sx; GLfloat sy;//缩放系数
void scale(wcPt2D *verts,GLfloat sx,GLfloat sy)
{
	//缩放函数，作为例子平移四边形
	GLint nverts = 4;
	wcPt2D fixedPt = verts[0];//选择左下的点作为基准点
	GLint k;
	wcPt2D newVerts[4];//使用一个新的顶点对象集，方便观察平移效果
	for (k = 0; k < nverts;++k)
	{
		newVerts[k].x = verts[k].x*sx+fixedPt.x*(1-sx)+200;//加200是为了水平平移200个像素，方便比较
		newVerts[k].y = verts[k].y*sy + fixedPt.y*(1 - sy);
	}
	
	glBegin(GL_QUADS);
	for (k = 0; k < nverts; ++k)
	{
		glVertex2f(verts[k].x, verts[k].y);
	}
	for (k = 0; k < nverts; ++k)
	{
		glVertex2f(newVerts[k].x, newVerts[k].y);
	}
	glEnd();

	glFlush();
}
void funcPlot()
{
	glClear(GL_COLOR_BUFFER_BIT);
	scale(verts,sx,sy);
}

结果：