LSTM理解
本文是对Nico’s blog Simple LSTM 翻译.
几个星期前,我在Github上发布了一些LSTM代码,以帮助人们了解LSTM在实现层面的工作方式。 前向传递在其他地方都有很好的解释并且很容易理解[可参考wangduo对LSTM翻译],但是我自己导出了backprop方程,并且backprop代码没有任何解释。 这篇文章的目的是在LSTM的背景下解释所谓的反向传播。
注意:本文假设您了解LSTM网络的正向传递,因为这部分相对简单。 如果您对此不熟悉,请阅读这篇精彩的介绍文章,因为它包含了一个非常好的LSTM介绍。 我遵循与本文相同的表示法,因此我建议阅读本教程时,在单独的浏览器选项卡中打开论文,以便在阅读本文时方便参考。
介绍:
LSTM节点的正向传递定义如下:
g
(
t
)
=
ϕ
(
W
g
x
x
(
t
)
+
W
g
h
h
(
t
−
1
)
+
b
g
)
i
(
t
)
=
σ
(
W
i
x
x
(
t
)
+
W
i
h
h
(
t
−
1
)
+
b
i
)
f
(
t
)
=
σ
(
W
f
x
x
(
t
)
+
W
f
h
h
(
t
−
1
)
+
b
f
)
o
(
t
)
=
σ
(
W
o
x
x
(
t
)
+
W
o
h
h
(
t
−
1
)
+
b
o
)
s
(
t
)
=
g
(
t
)
∗
i
(
t
)
+
s
(
t
−
1
)
∗
f
(
t
)
h
(
t
)
=
s
(
t
)
∗
o
(
t
)
begin{aligned} g(t) &=phileft(W_{g x} x(t)+W_{g h} h(t-1)+b_{g}right) \ i(t) &=sigmaleft(W_{i x} x(t)+W_{i h} h(t-1)+b_{i}right) \ f(t) &=sigmaleft(W_{f x} x(t)+W_{f h} h(t-1)+b_{f}right) \ o(t) &=sigmaleft(W_{o x} x(t)+W_{o h} h(t-1)+b_{o}right) \ s(t) &=g(t) * i(t)+s(t-1) * f(t) \ h(t) &=s(t) * o(t) end{aligned}
g(t)i(t)f(t)o(t)s(t)h(t)=ϕ(Wgxx(t)+Wghh(t−1)+bg)=σ(Wixx(t)+Wihh(t−1)+bi)=σ(Wfxx(t)+Wfhh(t−1)+bf)=σ(Woxx(t)+Wohh(t−1)+bo)=g(t)∗i(t)+s(t−1)∗f(t)=s(t)∗o(t)
上面公式表示图示为:
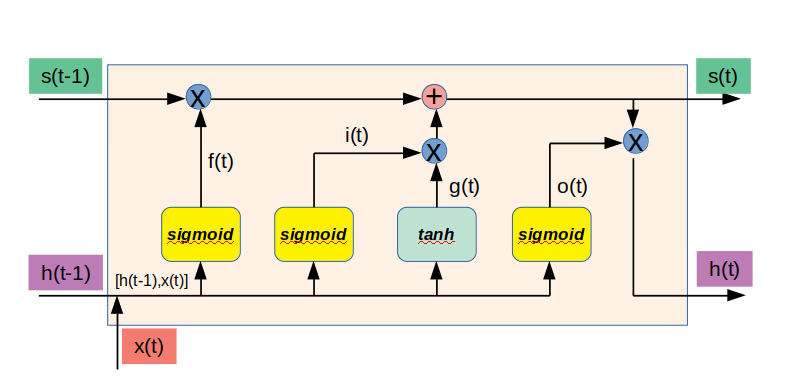
将
x
(
t
)
x(t)
x(t)和h(t-1)组合成为一个向量如下:
x
c
(
t
)
=
[
x
(
t
)
,
h
(
t
−
1
)
]
x_{c}(t)=[x(t), h(t-1)]
xc(t)=[x(t),h(t−1)]
我们可以重写上面的部分内容如下:
g
(
t
)
=
ϕ
(
W
g
x
c
(
t
)
+
b
g
)
i
(
t
)
=
σ
(
W
i
x
c
(
t
)
+
b
i
)
f
(
t
)
=
σ
(
W
f
x
c
(
t
)
+
b
f
)
o
(
t
)
=
σ
(
W
o
x
c
(
t
)
+
b
o
)
begin{aligned} g(t) &=phileft(W_{g} x_{c}(t)+b_{g}right) \ i(t) &=sigmaleft(W_{i} x_{c}(t)+b_{i}right) \ f(t) &=sigmaleft(W_{f} x_{c}(t)+b_{f}right) \ o(t) &=sigmaleft(W_{o} x_{c}(t)+b_{o}right) end{aligned}
g(t)i(t)f(t)o(t)=ϕ(Wgxc(t)+bg)=σ(Wixc(t)+bi)=σ(Wfxc(t)+bf)=σ(Woxc(t)+bo)
假设我们希望在每个时间步t处最小化的损失
l
(
t
)
l(t)
l(t)取决于通过隐藏层h和当前时刻的标签y得到的损失函数
f
f
f:
l
(
t
)
=
f
(
h
(
t
)
,
y
(
t
)
)
l(t)=f(h(t), y(t))
l(t)=f(h(t),y(t))
其中
f
f
f可以是任何可微分损失函数,例如欧几里德损失:
l
(
t
)
=
f
(
h
(
t
)
,
y
(
t
)
)
=
∥
h
(
t
)
−
y
(
t
)
∥
2
l(t)=f(h(t), y(t))=|h(t)-y(t)|^{2}
l(t)=f(h(t),y(t))=∥h(t)−y(t)∥2
在这种情况下,我们的最终目标是使用梯度下降最小化整个时间长度
T
T
T的损失L:
L
=
∑
t
=
1
T
l
(
t
)
L=sum_{t=1}^{T} l(t)
L=t=1∑Tl(t)
让我们通过计算损失函数的梯度:
d
L
d
w
frac{d L}{d w}
dwdL
其中
w
w
w是模型的标量参数(例如,它可以是矩阵
W
g
x
W_{gx}
Wgx)。 由于损失函数
l
(
t
)
=
f
(
h
(
t
)
,
y
(
t
)
)
l(t)=f(h(t),y(t))
l(t)=f(h(t),y(t))仅取决于隐藏层
h
(
t
)
h(t)
h(t)和标签
y
(
t
)
y(t)
y(t)的值,由于标签是常量,根据链式求导法则得到:
d
L
d
w
=
∑
t
=
1
T
∑
i
=
1
M
d
L
d
h
i
(
t
)
d
h
i
(
t
)
d
w
frac{d L}{d w}=sum_{t=1}^{T} sum_{i=1}^{M} frac{d L}{d h_{i}(t)} frac{d h_{i}(t)}{d w}
dwdL=t=1∑Ti=1∑Mdhi(t)dLdwdhi(t)
其中,
h
i
(
t
)
h_i(t)
hi(t)对应于第
i
i
i个存储器单元的隐藏输出的标量,
M
M
M是每个存储器单元的总数,由于网络在时间上向前传播信息,因此
h
i
(
t
)
h_i(t)
hi(t)对时间t之前的损失没有影响,因此,如下:
d
L
d
h
i
(
t
)
=
∑
s
=
1
T
d
l
(
s
)
d
h
i
(
t
)
=
∑
s
=
t
T
d
l
(
s
)
d
h
i
(
t
)
frac{d L}{d h_{i}(t)}=sum_{s=1}^{T} frac{d l(s)}{d h_{i}(t)}=sum_{s=t}^{T} frac{d l(s)}{d h_{i}(t)}
dhi(t)dL=s=1∑Tdhi(t)dl(s)=s=t∑Tdhi(t)dl(s)
为方便起见,我们引入变量
L
(
t
)
L(t)
L(t),表示从步骤t开始的累积损失:
L
(
t
)
=
∑
s
=
t
s
=
T
l
(
s
)
L(t)=sum_{s=t}^{s=T} l(s)
L(t)=s=t∑s=Tl(s)
这样
L
(
1
)
L(1)
L(1)就是整个序列的损失,这允许我们将上面的等式重写为:
d
L
d
h
i
(
t
)
=
∑
s
=
t
T
d
l
(
s
)
d
h
i
(
t
)
=
d
L
(
t
)
d
h
i
(
t
)
frac{d L}{d h_{i}(t)}=sum_{s=t}^{T} frac{d l(s)}{d h_{i}(t)}=frac{d L(t)}{d h_{i}(t)}
dhi(t)dL=s=t∑Tdhi(t)dl(s)=dhi(t)dL(t)
考虑到这一点,我们可以重新编写梯度计算公式:
d
L
d
w
=
∑
t
=
1
T
∑
i
=
1
M
d
L
(
t
)
d
h
i
(
t
)
d
h
i
(
t
)
d
w
frac{d L}{d w}=sum_{t=1}^{T} sum_{i=1}^{M} frac{d L(t)}{d h_{i}(t)} frac{d h_{i}(t)}{d w}
dwdL=t=1∑Ti=1∑Mdhi(t)dL(t)dwdhi(t)
确保你理解这最后的等式.
d
h
i
(
t
)
d
w
frac{dh_i(t)}{dw}
dwdhi(t) 的计算直接遵循前面给出的前向传播方程。 我们现在展示如何计算
d
L
(
t
)
d
h
i
(
t
)
frac{dL(t)}{dh_i(t)}
dhi(t)dL(t),这是所谓的反向传播随着时间发挥作用的地方。
随时间的反向传播
这个变量
L
(
t
)
L(t)
L(t)允许我们表达以下递归:
L
(
t
)
=
{
l
(
t
)
+
L
(
t
+
1
)
if
t
<
T
l
(
t
)
if
t
=
T
L(t)=left{begin{array}{ll}{l(t)+L(t+1)} & {text { if } t<T} \ {l(t)} & {text { if } t=T}end{array}right.
L(t)={l(t)+L(t+1)l(t) if t<T if t=T
因此,给定LSTM节点在时间t的激活
h
(
t
)
h(t)
h(t),我们就有了:
d
L
(
t
)
d
h
(
t
)
=
d
l
(
t
)
d
h
(
t
)
+
d
L
(
t
+
1
)
d
h
(
t
)
frac{d L(t)}{d h(t)}=frac{d l(t)}{d h(t)}+frac{d L(t+1)}{d h(t)}
dh(t)dL(t)=dh(t)dl(t)+dh(t)dL(t+1)
现在,我们知道右边的第一项
d
l
(
t
)
d
h
(
t
)
frac{dl(t)}{dh(t)}
dh(t)dl(t)来自何处:它是损失函数
l
(
t
)
l(t)
l(t)相对于时刻t的激活
h
(
t
)
h(t)
h(t)的导数.第二项
d
L
(
t
+
1
)
d
h
(
t
)
frac{dL(t+1)}{dh(t)}
dh(t)dL(t+1)是LSTM迭代性质的表现,表明我们需要下一个节点的导数信息,以便计算出当前节点的导数信息,因此我们需要计算
t
=
1
,
.
.
.
,
T
t=1,...,T
t=1,...,T的
d
L
(
t
)
d
h
(
t
)
frac{dL(t)}{dh(t)}
dh(t)dL(t)值,首先开始计算:
d
L
(
T
)
d
h
(
T
)
=
d
l
(
T
)
d
h
(
T
)
frac{d L(T)}{d h(T)}=frac{d l(T)}{d h(T)}
dh(T)dL(T)=dh(T)dl(T)
并通过网络向后工作。 因此,反向传播随着时间的推移。 有了这些基础,我们可以跳进代码。
代码
我们现在提供在1≤t≤T时执行backprop传递通过单个节点的代码。
代码输入:
-
top_diff_h= d L ( t ) d h ( t ) = d l ( t ) d h ( t ) + d L ( t + 1 ) d h ( t ) frac{d L(t)}{d h(t)}=frac{d l(t)}{d h(t)}+frac{d L(t+1)}{d h(t)} dh(t)dL(t)=dh(t)dl(t)+dh(t)dL(t+1)
-
top_diff_h= d L ( t + 1 ) d s ( t ) frac{d L(t+1)}{d s(t)} ds(t)dL(t+1)
计算输出:
- self.state.bottom_diff_s= d L ( t ) d s ( t ) frac{d L(t)}{d s(t)} ds(t)dL(t)
- self.state.bottom_diff_h= d L ( t ) d h ( t − 1 ) frac{d L(t)}{d h(t-1)} dh(t−1)dL(t)
其值需要及时向后传播,该代码还添加了衍生物:
- self.param.wi_diff= d L d W i frac{d L}{dW_i} dWidL
- …
- self.param.bi_diff= d L d b i frac{d L}{db_i} dbidL
- …
自反向计算以来,我们必须总结每个时间步的衍生物:
d L d w = ∑ t = 1 T ∑ i = 1 M d L ( t ) d h i ( t ) d h i ( t ) d w frac{d L}{d w}=sum_{t=1}^{T} sum_{i=1}^{M} frac{d L(t)}{d h_{i}(t)} frac{d h_{i}(t)}{d w} dwdL=t=1∑Ti=1∑Mdhi(t)dL(t)dwdhi(t)
另外,请注意我们使用:- dxc = d L d x c ( t ) text{dxc}=frac{d L}{dx_c(t)} dxc=dxc(t)dL
其中, x c ( t ) = [ x ( t ) , h ( t − 1 ) ] x_{c}(t)=[x(t), h(t-1)] xc(t)=[x(t),h(t−1)]
代码如下:
def top_diff_is(self, top_diff_h, top_diff_s): # notice that top_diff_s is carried along the constant error carousel ds = self.state.o * top_diff_h + top_diff_s do = self.state.s * top_diff_h di = self.state.g * ds dg = self.state.i * ds df = self.s_prev * ds # diffs w.r.t. vector inside sigma / tanh function di_input = sigmoid_derivative(self.state.i) * di df_input = sigmoid_derivative(self.state.f) * df do_input = sigmoid_derivative(self.state.o) * do dg_input = tanh_derivative(self.state.g) * dg # diffs w.r.t. inputs self.param.wi_diff += np.outer(di_input, self.xc) self.param.wf_diff += np.outer(df_input, self.xc) self.param.wo_diff += np.outer(do_input, self.xc) self.param.wg_diff += np.outer(dg_input, self.xc) self.param.bi_diff += di_input self.param.bf_diff += df_input self.param.bo_diff += do_input self.param.bg_diff += dg_input # compute bottom diff dxc = np.zeros_like(self.xc) dxc += np.dot(self.param.wi.T, di_input) dxc += np.dot(self.param.wf.T, df_input) dxc += np.dot(self.param.wo.T, do_input) dxc += np.dot(self.param.wg.T, dg_input) # save bottom diffs self.state.bottom_diff_s = ds * self.state.f self.state.bottom_diff_h = dxc[self.param.x_dim:]细节
前向传播公式表明, s ( t ) s(t) s(t)的值通过改变 h ( t ) h(t) h(t)或者 h ( t + 1 ) h(t+1) h(t+1)来影响损失函数 L ( t ) L(t) L(t),对 s ( t ) s(t) s(t)的求导法则:
d L ( t ) d s i ( t ) = d L ( t ) d h i ( t ) d h i ( t ) d s i ( t ) + d L ( t ) d h i ( t + 1 ) d h i ( t + 1 ) d s i ( t ) = d L ( t ) d h i ( t ) d h i ( t ) d s i ( t ) + d L ( t + 1 ) d h i ( t + 1 ) d h i ( t + 1 ) d s i ( t ) = d L ( t ) d h i ( t ) d h i ( t ) d s i ( t ) + d L ( t + 1 ) d s i ( t ) = d L ( t ) d h i ( t ) d h i ( t ) d s i ( t ) + [ t o p _ d i f f _ s ] i begin{aligned} frac{d L(t)}{d s_{i}(t)} &=frac{d L(t)}{d h_{i}(t)} frac{d h_{i}(t)}{d s_{i}(t)}+frac{d L(t)}{d h_{i}(t+1)} frac{d h_{i}(t+1)}{d s_{i}(t)} \ &=frac{d L(t)}{d h_{i}(t)} frac{d h_{i}(t)}{d s_{i}(t)}+frac{d L(t+1)}{d h_{i}(t+1)} frac{d h_{i}(t+1)}{d s_{i}(t)} \ &=frac{d L(t)}{d h_{i}(t)} frac{d h_{i}(t)}{d s_{i}(t)}+frac{d L(t+1)}{d s_{i}(t)} \ &=frac{d L(t)}{d h_{i}(t)} frac{d h_{i}(t)}{d s_{i}(t)}+left[{top_diff_s}right]_{i} end{aligned} dsi(t)dL(t)=dhi(t)dL(t)dsi(t)dhi(t)+dhi(t+1)dL(t)dsi(t)dhi(t+1)=dhi(t)dL(t)dsi(t)dhi(t)+dhi(t+1)dL(t+1)dsi(t)dhi(t+1)=dhi(t)dL(t)dsi(t)dhi(t)+dsi(t)dL(t+1)=dhi(t)dL(t)dsi(t)dhi(t)+[top_diff_s]i
由于前向传播方程为:
h ( t ) = s ( t ) ∗ o ( t ) h(t)=s(t) * o(t) h(t)=s(t)∗o(t)
可得:
d L ( t ) d h i ( t ) d h i ( t ) d s i ( t ) = o i ( t ) ∗ [ t o p _ d i f f _ h ] frac{d L(t)}{d h_{i}(t)}frac{d h_{i}(t)}{d s_{i}(t)}=o_{i}(t) *[top_diff_h] dhi(t)dL(t)dsi(t)dhi(t)=oi(t)∗[top_diff_h]
将上述结果放在一起:ds = self.state.o * top_diff_h + top_diff_s
最后
以上就是单纯钢铁侠最近收集整理的关于LSTM python 实现理解LSTM理解的全部内容,更多相关LSTM内容请搜索靠谱客的其他文章。








发表评论 取消回复