1. 首页
  2. 文章中心
  3. rnn

NNDL 实验七 循环神经网络（3）LSTM的记忆能力实验6.3 LSTM的记忆能力实验全面总结RNN（必做）

68 阅读 0 评论
我是靠谱客的博主 执着菠萝，最近开发中收集的这篇文章主要介绍NNDL 实验七 循环神经网络（3）LSTM的记忆能力实验6.3 LSTM的记忆能力实验全面总结RNN（必做），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

6.3 LSTM的记忆能力实验

使用LSTM模型重新进行数字求和实验，验证LSTM模型的长程依赖能力。

6.3.1 模型构建

使用第6.1.2.4节中定义Model_RNN4SeqClass模型，并构建 LSTM 算子．

只需要实例化 LSTM ，并传入Model_RNN4SeqClass模型，就可以用 LSTM 进行数字求和实验。

6.3.1.1 LSTM层

自定义LSTM算子
nn.LSTM
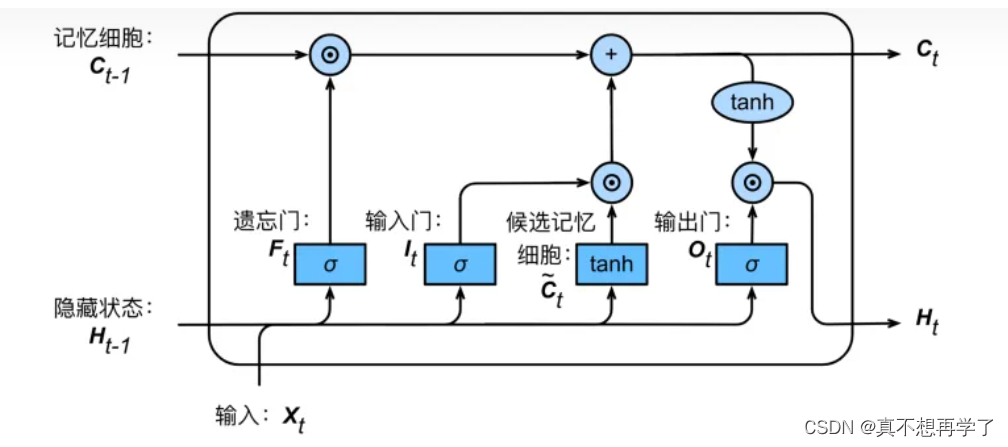
在这里插入图片描述

相较于简单的RNNcell，LSTMcell有着更为复杂的结构，包括三个门，一个记忆单元，根据LSTM的结构，现定义LSTMcell类，代替之前的RNNcell类。

class LSTMCell(nn.Module):

    def __init__(self, input_size, hidden_size, bias=True):
        super(LSTMCell, self).__init__()
        self.input_size = input_size
        self.hidden_size = hidden_size
        self.bias = bias
        self.x2h = nn.Linear(input_size, hidden_size, bias=bias)
        self.h2h = nn.Linear(hidden_size, hidden_size, bias=bias)
        self.reset_parameters()

    def reset_parameters(self):
        std = 1.0 / math.sqrt(self.hidden_size)
        for w in self.parameters():
            w.data.uniform_(-std, std)

    def forward(self, x, hidden):
        hx=hidden
        cx = hidden

        gates = self.x2h(x) + self.h2h(hx)

        gates = gates.squeeze()
        ingate = torch.sigmoid(gates)
        forgetgate = torch.sigmoid(gates)
        cellgate = torch.tanh(gates)
        outgate = torch.sigmoid(gates)

        cy = torch.mul(cx, forgetgate) + torch.mul(ingate, cellgate)

        hy = torch.mul(outgate, torch.tanh(cy))

        return (hy, cy)

将自定义LSTM与pytorch内置的LSTM进行对比
自定义LSTM：

class number_Sum_model(torch.nn.Module):
    def __init__(self,input_size, hidden_size,seq_len):
        super(number_Sum_model, self).__init__()
        self.linear=torch.nn.Linear(hidden_size,19)
        self.sigmoid=torch.nn.Sigmoid()
        self.input_size=input_size
        self.norm_in=torch.nn.BatchNorm1d(input_size)
        self.norm_h = torch.nn.BatchNorm1d(hidden_size)
        self.seq_len=seq_len
        self.lstm=LSTMCell(input_size=input_size, hidden_size=hidden_size)

    def forward(self,X):
        #print('---------input--------')
        #print(X)
        num=0
        for i in range(self.seq_len):
            x_in=X[i,:]
            #print('------num %4d in seq:------'%num)
            #print(x_in)
            num+=1
            if i==0:
                c0=torch.randn(size=x_in.shape)
                h1,c1 = self.lstm.forward(x_in,c0)
            else:
                h1,c1=self.lstm.forward(x_in,c1)

        outh=self.linear(h1)
        return outh

6.3.2 模型训练

训练过程与基本的网络训练过程没什么区别，代码如下：

def train():
    net =number_Sum_model(input_size=10,hidden_size=10,seq_len=seq_len)
    epoches=1000
    running_loss=0
    loss_list=[]
    t_loss_list=[]
    optim = torch.optim.Adam(net.parameters(), lr=0.001)
    loss = torch.nn.CrossEntropyLoss()
    for epoch in range(epoches):
        epoch_loss=0
        for x,t in zip(train_X,target):
            out = net.forward(x)
            #print('------target------')
            #print(t)
            l=loss(out,t)
            l.backward()
            optim.step()
            optim.zero_grad()
            running_loss+=l
            epoch_loss+=l.detach().numpy()
        loss_list.append(epoch_loss)
        test_loss=0
        for x,t,in zip(test_X,test_target):
            out=net.forward(x)
            t_loss=loss(out,t)
            test_loss+=t_loss.detach().numpy()
        t_loss_list.append(test_loss)
        if epoch %100 == 0:
            print('===============epoch=%5d===================' % (epoch))
            print('----------------current output:-----------------')
            print(out.shape)
            print('[train] [epoch:%4d/%4d] current loss: %.8f,current epoch loss:%.8f,total loss:%.8f'
                  % (epoch + 1, epoches, l.item(),epoch_loss, running_loss))
            print('[test] accuracy in train data:%.8f %%'%(test(net, train_X, target)*100))
            print('[test] accuracy in test data:%.8f %%' % (test(net, test_X, test_target) * 100))

6.3.2.1 训练指定长度的数字预测模型

一共有6种序列长度，对应SRN训练，有5，10，15，20，25，30共6种。数据集的生成部分和处理部分参见SRN长程记忆实验部分。
主要用到的函数：
处理输入数据，进行独热编码并转换成tensor

def set_data(X):
    o_X=[]
    for x in X:
        target_list = []
        for target in x:
            if target == 0:
                target_list.append(torch.Tensor([1, 0, 0, 0, 0, 0, 0, 0, 0, 0]))
            elif target == 1:
                target_list.append(torch.Tensor([0, 1, 0, 0, 0, 0, 0, 0, 0, 0]))
            elif target == 2:
                target_list.append(torch.Tensor([0, 0, 1, 0, 0, 0, 0, 0, 0, 0]))
            elif target == 3:
                target_list.append(torch.Tensor([0, 0, 0, 1, 0, 0, 0, 0, 0, 0]))
            elif target == 4:
                target_list.append(torch.Tensor([0, 0, 0, 0, 1, 0, 0, 0, 0, 0]))
            elif target == 5:
                target_list.append(torch.Tensor([0, 0, 0, 0, 0, 1, 0, 0, 0, 0]))
            elif target == 6:
                target_list.append(torch.Tensor([0, 0, 0, 0, 0, 0, 1, 0, 0, 0]))
            elif target == 7:
                target_list.append(torch.Tensor([0, 0, 0, 0, 0, 0, 0, 1, 0, 0]))
            elif target == 8:
                target_list.append(torch.Tensor([0, 0, 0, 0, 0, 0, 0, 0, 1, 0]))
            elif target==9:
                target_list.append(torch.Tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 1]))
        X_list = torch.stack(target_list)
        o_X.append(X_list)
    output=torch.stack(o_X)
    return torch.squeeze(output)

处理输出数据，进行独热编码并转换成tensor

def set_target(X):
    o_X = []
    for x in X:
        target_list = []
        for target in x:
            if target == 0:
                target_list.append(torch.Tensor([1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]))
            elif target == 1:
                target_list.append(torch.Tensor([0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]))
            elif target == 2:
                target_list.append(torch.Tensor([0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]))
            elif target == 3:
                target_list.append(torch.Tensor([0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]))
            elif target ==4:
                target_list.append(torch.Tensor([0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]))
            elif target == 5:
                target_list.append(torch.Tensor([0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]))
            elif target == 6:
                target_list.append(torch.Tensor([0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]))
            elif target == 7:
                target_list.append(torch.Tensor([0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]))
            elif target == 8:
                target_list.append(torch.Tensor([0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]))
            if target == 9:
                target_list.append(torch.Tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]))
            elif target == 10:
                target_list.append(torch.Tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0]))
            elif target == 11:
                target_list.append(torch.Tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0]))
            elif target == 12:
                target_list.append(torch.Tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0]))
            elif target == 13:
                target_list.append(torch.Tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0]))
            elif target == 14:
                target_list.append(torch.Tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0]))
            elif target == 15:
                target_list.append(torch.Tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0]))
            elif target == 16:
                target_list.append(torch.Tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0]))
            elif target == 17:
                target_list.append(torch.Tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0]))
            elif target==18:
                target_list.append(torch.Tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]))
        X_list = torch.stack(target_list)
        o_X.append(X_list)
    output=torch.stack(o_X)
    return torch.squeeze(output)

测试网络，指标为正确率

def test(model, X, y):
    T=0
    for x in X:
        pre_y = model(x)
        max_pre_y = torch.argmax(pre_y, dim=0)
        max_y = torch.argmax(y, dim=0)
        acc=torch.nonzero(max_y.eq(max_pre_y)).shape[0]
        T+=acc
    return T/target.shape[0]

随机生成数据集

def get_data(seq_len):
    outx=[]
    outy=[]
    for i in range(10):
        for j in range(10):
            tmp=[i,j]+random_num(seq_len-2)
            outx.append(tmp)
            outy.append(i+j)
    return outx,outy

def random_num(num):
    list=[]
    for i in range(num):
        pool=[i for i in range(10)]+[0]*90
        list.append(random.choice(pool))
    return list

6.3.2.3 损失曲线展示

采用边训练边绘制的方法，最后一并输出。

        print('-------------------training ended.----------------')
        print('-------------------test---------------------')
        plt.subplot(2,3,i+1)
        plt.plot(range(epoches),loss_list,label='loss in train data')
        plt.plot(range(epoches),t_loss_list,label='loss in test data')
        plt.legend()
        plt.xlabel('epoches')
        plt.ylabel('loss')
        plt.title('seq_lenth={}'.format(seq_len))
    plt.show()

6.3.3 模型评价

6.3.3.1 在测试集上进行模型评价

【思考题1】LSTM与SRN实验结果对比，谈谈看法。（选做）

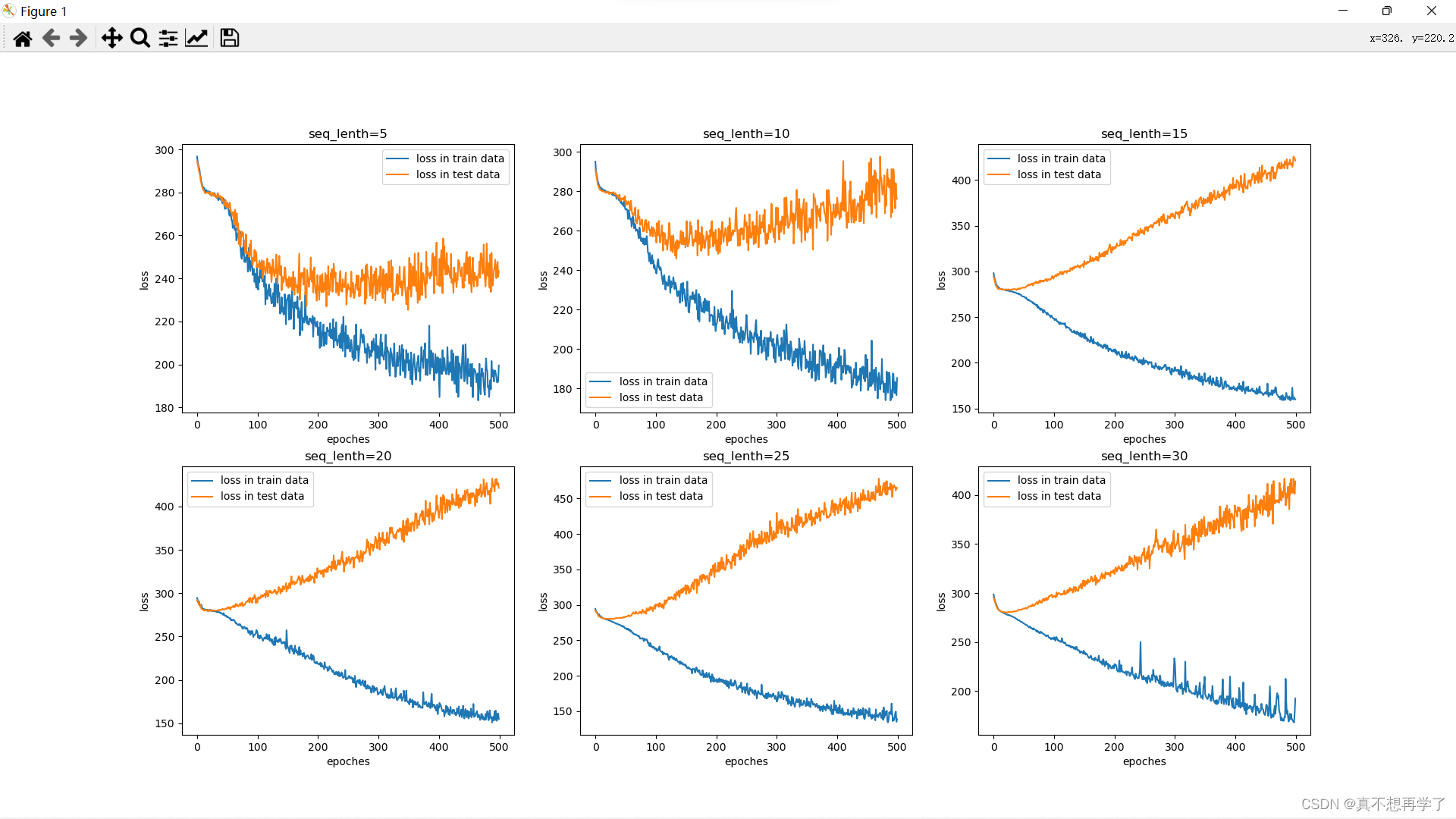在这里插入图片描述对比SRN’（将隐藏层数降低到了10）的结果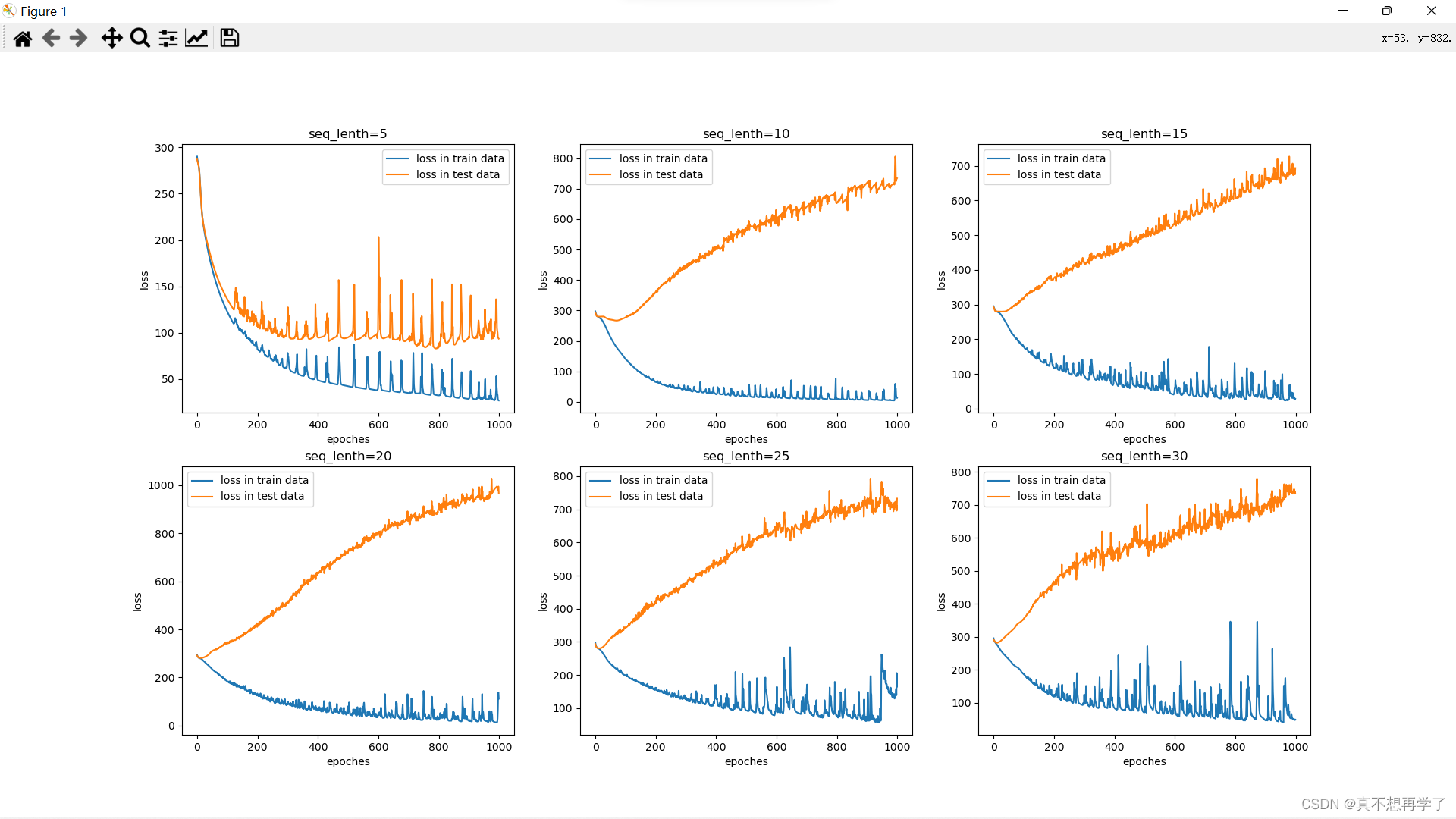在这里插入图片描述

可以看到，LSTM的损失要明显低于SRN，虽然效果没有那么神奇，但很明显在前几次都是LSTM占优的，后几个也是损失要低于SRN的，而且LSTM只运行了500次，运行多了的话会内存满了然后终止训练。
相较于SRN的简单cell模型，LSTMcell添加了三个门和一个状态单元，拥有更加复杂多变的网络结构，而且还添加了一条总线，增加了模型的长程记忆能力，这也是为什么LSTM能够更好的分类较长干扰序列的主要原因。
为了便于观察，还是按照邱老师的这个结果作为对比：
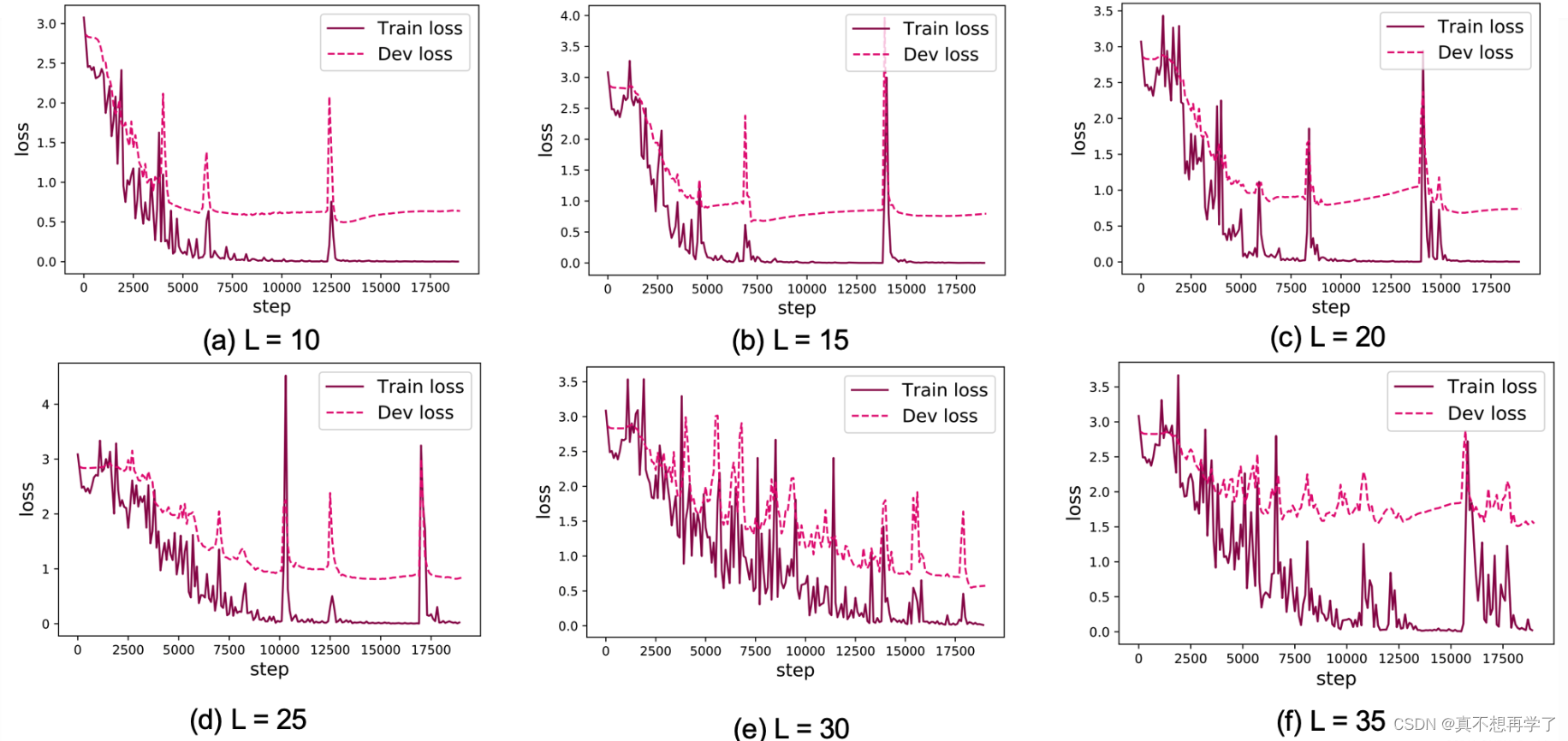
在这里插入图片描述
这个就非常具有代表性；他的长序列分类在测试集上的损失就明显要比SRN的要低 ，它几乎是贴近在训练集上的损失的。
由于LSTMcell本身就设计的很复杂，导致这也很难说清楚它到底是怎样实现的，大体上，就是通过遗忘门将干扰序列给遗忘掉了，或者说是将原来的记忆用新的记忆冲刷掉了，这个过程通过一次逻辑运算实现；输入门决定是否将信息输入到长程状态记忆中，状态单元则是储存了当前的状态，两者的卷积实际上像是挑选出了有用的东西加到总线上；最后的输出门则是利用上了总线上的信息，对输入进行处理并输出，这时候的总线已经包含了输入的很多信息（因为已经经过了两次处理，一次遗忘门，一次状态输入），同时又包含了总线上的之前信息，就这样在此基础上，进一步增强了网络对长程信息记忆的能力。网络越长，优势就越明显。
（纯属个人理解，如有错误请多指出。）

【思考题2】LSTM与SRN在不同长度数据集上的准确度对比，谈谈看法。（选做）

6.3.3.3 LSTM模型门状态和单元状态的变化

【思考题3】分析LSTM中单元状态和门数值的变化图，并用自己的话解释该图。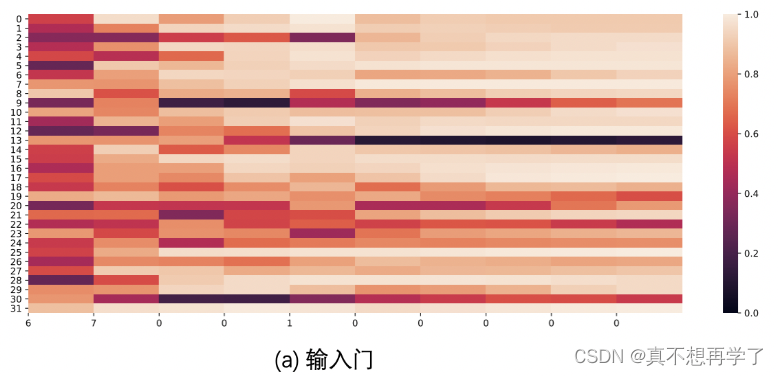在这里插入图片描述

输入门需要与单元状态进行一次相关运算，它的值决定了状态门的某些是否需要输入到长程总线中，从而对主线进行调整

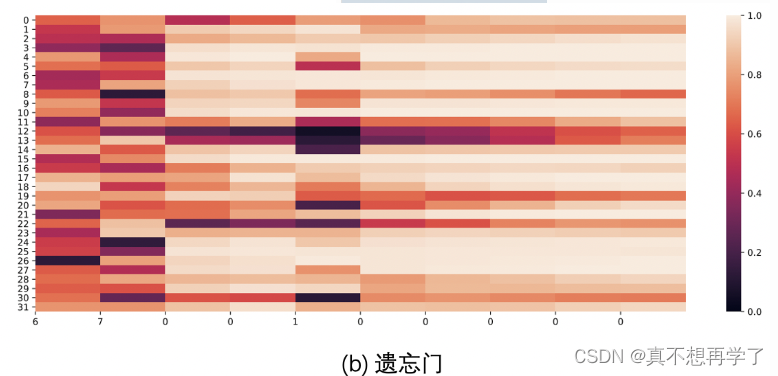
在这里插入图片描述
遗忘门决定是否对总线信息进行冲洗，热力图中的和总线上面的值差别越大，总线信息被冲洗的越厉害，可以看到随着迭代次数增加，他的值是区域稳定的。
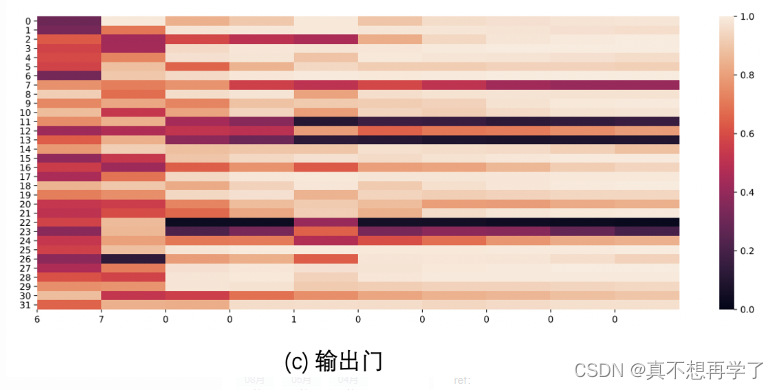
在这里插入图片描述
输出门会与总线进行一次相关运算，将总线信息（它包含的经验）利用上，从而输出下一个隐藏状态的值，随着迭代层数的增加，网络的输出值也是趋于稳定的。
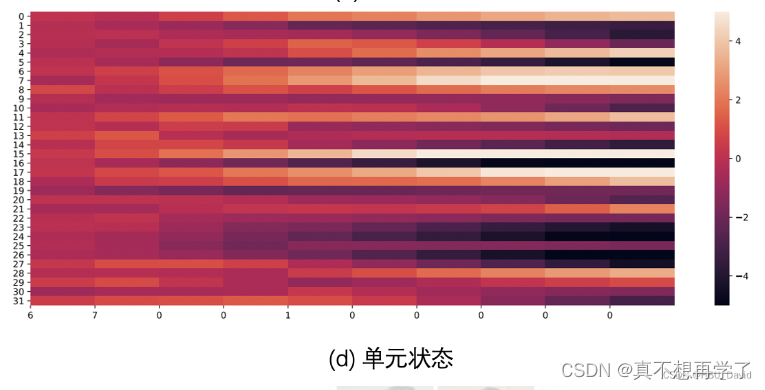
在这里插入图片描述
经过一次tanh，降至约束到了大约-5~5之间，它是当前的状态，也就是候选记忆的存储位置，他会与输入门进行一次相关运算，被挑选出有用的信息加入长程总线之中。

LSTM有一个长期总线和一个短期记忆单元，所以被称为长短期网络模型，实际上，他的短期记忆功能似乎也体现于他的隐状态之中，因为它里面也存储了短期的网络信息。

全面总结RNN（必做）

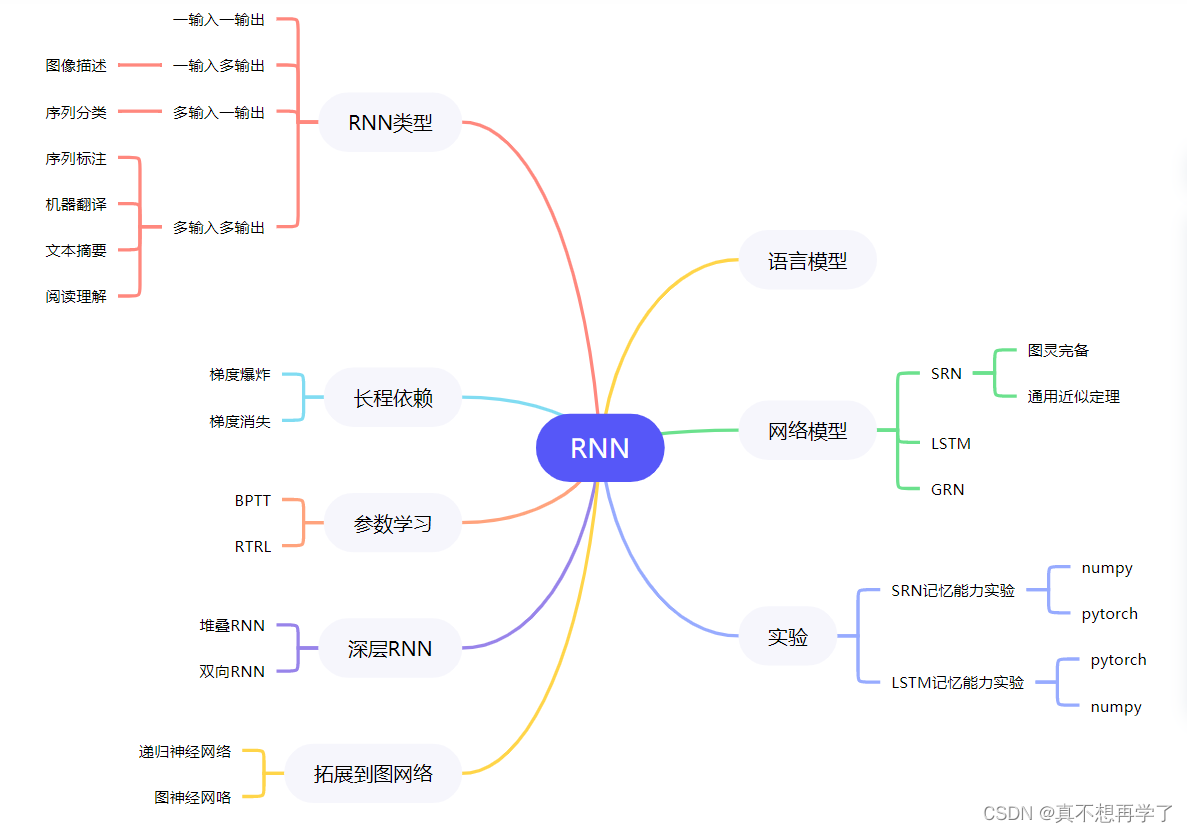
在这里插入图片描述

最后

以上就是执着菠萝为你收集整理的NNDL 实验七 循环神经网络（3）LSTM的记忆能力实验6.3 LSTM的记忆能力实验全面总结RNN（必做）的全部内容，希望文章能够帮你解决NNDL 实验七 循环神经网络（3）LSTM的记忆能力实验6.3 LSTM的记忆能力实验全面总结RNN（必做）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(45)

相关文章

python基础教程：Python中利用LSTM模型进行时间序列预测分析的实现
python基础教程：Python中利用LSTM模型进行时间序列预测分析的实现
5G多址技术何去何从?
5G多址技术何去何从?
python之LSTM预测模型
python之LSTM预测模型
python利用LSTM进行时间序列分析预测
python利用LSTM进行时间序列分析预测
NNDL 实验七 循环神经网络（3）LSTM的记忆能力实验6.3 LSTM的记忆能力实验全面总结RNN（必做）
NNDL 实验七 循环神经网络（3）LSTM的记忆能力实验6.3 LSTM的记忆能力实验全面总结RNN（必做）
lstm预测模型_Python实现多变量序列堆叠式LSTM模型，并实现未来多时刻预测
lstm预测模型_Python实现多变量序列堆叠式LSTM模型，并实现未来多时刻预测
LSTM python 实现理解LSTM理解
LSTM python 实现理解LSTM理解
无线电信号调制【小波去噪】（Matlab&Python代码实现）
无线电信号调制【小波去噪】（Matlab&Python代码实现）

评论列表共有 0 条评论

立即
投稿
返回
顶部