【转载请注明出处:http://blog.csdn.net/leytton/article/details/40380753】
%功能:多项式求解
%建立向量X,各元素为多项式按降幂排列时系数,默认项为0,不得省略
% 如 y=x^3+4*x+12 表示为X=[1 0 4 12];
% y=x^2-9 表示为 X=[1 0 -9]; y=3x+6 表示为 X=[3 6];
% roots(X) 即为 y=0 的解
X=[1 0 -9];
roots(X)
X=[3 6];
roots(X)
%功能:多项式乘积
%y1=2*x^2+3x+1 y2=x+6
y1=[2 3 1];
y2=[1 6];
y=conv(y1,y2) %y=y1*y2
polyval(y,4) %当x=4时求y的值
%功能:多项式拟合
clear all;
x=[0 1 2 3 4 5];
y=[2 1 3 2 5 8];
P2=polyfit(x,y,2);
P8=polyfit(x,y,8);
%y2=polyval(P2,x(1):0.01:x(end));
y2=polyval(P2,x);
y8=polyval(P8,x);
plot(x,y,'*');
hold on
%plot(x(1):0.01:x(end),y2,'x');
%plot画图的颜色线型 http://blog.sina.com.cn/s/blog_4d8716e401000apg.html
plot(x,y2,'r:');
plot(x,y8,'c-');
ylim([0,8]);
clear all;
t=0:pi/50:5*pi;
y0=exp(-t/4);
y=exp[(-t/4).*sin(4*t)];
plot(t,y,'-r')
摘自 http://blog.csdn.net/wenqisun/article/details/7952476
多项式拟合
polyfit(X,Y,N):多项式拟合,返回降幂排列的多项式系数。
polyval(P,xi):计算多项式的值。
其中,X,Y是数据点的值;N是拟合的最高次幂;P是返回的多项式系数;xi是要求的点的横坐标。
x=[1 2 3 4 5 6 7 8 9]
y=[9 7 6 3 -1 2 5 7 20]
P=polyfit(x,y,3);
xi=0:.2:10;
yi=polyval(P,xi);
plot(xi,yi,x,y,'r*');摘自 http://jingyan.baidu.com/article/6c67b1d6eee2dc2787bb1eb5.html
poly---特征多项式
格式:poly(a)
(1)如果a是一个n阶矩阵,poly(a)是一个有n+1个元素的行向量,这n+1个元素是特征多项式的系数(降幂排列).
(2)如果a是一个n维向量,则poly(a)是多项式(x-a(1))*(x-a(2))*..(x-a(n)),即该多项式以向量a的元素为根。
摘自 http://jingyan.baidu.com/article/a3aad71aaff6edb1fb009684.html
特定点数值求解
对于给定的多项式表达式,比如f(x),求特定点(x0)值,可以采用polyval函数。
% polyval
% y = x^5 + 4*x^3 + 2*x^2 + x + 1
p = [1 0 4 2 1 1];
y1 = polyval(p,1)
其中,在表达多项式时,其实只需要表示出各项系数。计算结果如下所示:
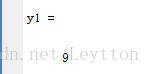
多项式相乘
对于给定的多项式p1与p2,可以利用conv函数快速求解其乘积值:
% conv
% y1 = x^5 + 4*x^3 + 2*x^2 + x + 1
% y2 = x^2 + 4*x + 2
p1 = [1 0 4 2 1 1];
p2 = [1 4 2];
p = conv(p1,p2)
其中输出结果如下:

参数化显示多项式
在数学分析与书写时,我们习惯于参数化多项式,也就是含有变量的式子,可利用poly2str函数。
% poly2str
% y = 5*x^3 + 2*x + 3
p = [5 0 2 3];
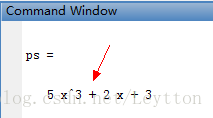
ps = poly2str(p,'x')
根(零点)求解
在多项式分析时,常需要求解根,可使用roots指令。
% roots
% y = 5*x^4 + 4*x^2 + 2*x + 4
p = [5 0 4 2 4];
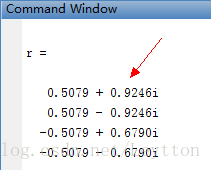
r = roots(p)
由于方程系数为4阶,可以求得4个实根。如下图所示:
多项式相除
有时候需要进行多项式之间除法,例如 p = p1 / p2 ,其中p1,p2为两个多项式,可以借助于deconv函数实现。
% roots
% y1 = 3*x^4 + 4*x^2 + 2*x + 6
% y2 = 5*x^2 + x + 3
p1 = [3 0 4 2 6];
p2 = [5 1 3];
[p,r] = deconv(p1,p2)
其中,p是相除后的商,而r为余数。

转载于:https://www.cnblogs.com/leytton/p/8253347.html
最后
以上就是饱满热狗最近收集整理的关于《MATLAB与系统仿真》 多项式的全部内容,更多相关《MATLAB与系统仿真》内容请搜索靠谱客的其他文章。








发表评论 取消回复