冲激信号的卷积性质&采样信号频谱的周期性延拓

1. 冲激信号的卷积

由冲激信号的卷积性质可知：冲激信号具有显像性。

任何信号对单位冲激函数的卷积等于该信号本身，那么单位冲激函数就相当于是一种“显像”信号，当冲激函数对冲激函数卷积时，就相当于将其中的一个冲激函数显像出来。

clc,clear,close all;
x = [1,zeros(1,9)]      %信号1，作为冲激信号
h = [-2:1:2]              %信号2
nx = [1:10];nh = [-2:2];  %序列下标
disp(length(x));
disp(length(h));
[y,ny] = convu(x,nx,h,nh)
stem(ny,y,"linewidth",2);

function[y,ny]=convu(h,nh,x,nx)
nys = nh(1)+nx(1);     %卷积的起始点
nyf = nh(end)+nx(end); %卷积的终止点
y = conv(h,x); ny=nys:nyf;
end

运行结果如下图所示：

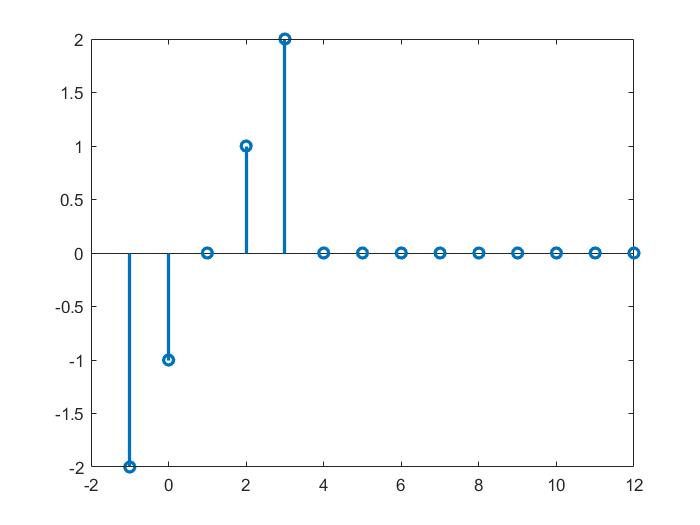
信号1可看做$\delta (n)$，与信号2做卷积。

clc,clear,close all;
x = [0,1,zeros(1,8)]      %信号1，作为冲激信号
h = [-2:1:2]              %信号2
nx = [1:10];nh = [-2:2];  %序列下标
disp(length(x));
disp(length(h));
[y,ny] = convu(x,nx,h,nh)
stem(ny,y,"linewidth",2);

function[y,ny]=convu(h,nh,x,nx)
nys = nh(1)+nx(1);     %卷积的起始点=信号1起始点+信号2起始点
nyf = nh(end)+nx(end); %卷积的终止点=信号1终止点+信号2终止点
y = conv(h,x); ny=nys:nyf;
end

运行结果如下图所示：

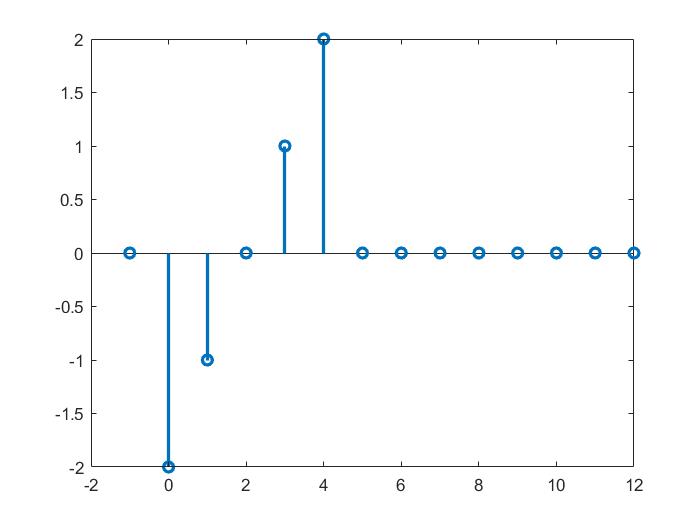
信号2的取值为[-2,-1,0,1,2]，信号1可看做$\delta (n-1)$.

对比第一幅图，两者作卷积相当于将信号2向右平移一个单位。

2. 性质:

我们知道：

两个信号在时域乘积的傅里叶变换等于两个信号分别的傅里叶变换的卷积。

3. 仿真验证：

通过以下程序得以验证：

clc,clear,close all;
x = [1,zeros(1,10),1,zeros(1,10)]      %信号1，作为冲激信号
h = [zeros(1,7),-2:1:2,zeros(1,10)]             %信号2
nx = [1:length(x)];nh = [-9:12];       %序列下标
xn = fft(x,32); hn=fft(h,32);
disp(length(x));
disp(length(h));
[y,ny] = convu(x,nx,h,nh)
yn = fft(y,32);        %对卷积结果进行傅里叶变换
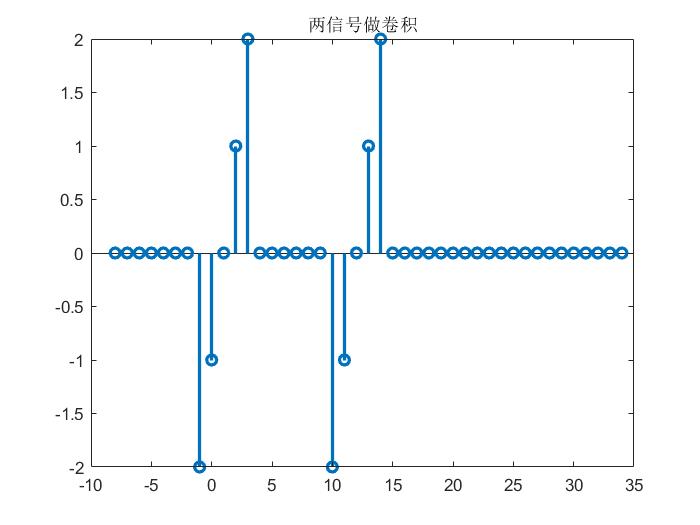
stem(ny,y,"linewidth",2);
title("两信号做卷积")
figure(2)
stem(fftshift(abs(xn.*hn)),"linewidth",2);
title("两信号分别做傅里叶变换后相乘")
figure(3)
stem(fftshift(abs(yn)),"linewidth",2);
title("两信号做卷积后的傅里叶变换")

function[y,ny]=convu(h,nh,x,nx)
nys = nh(1)+nx(1);     %卷积的起始点
nyf = nh(end)+nx(end); %卷积的终止点
y = conv(h,x); ny=nys:nyf;
end

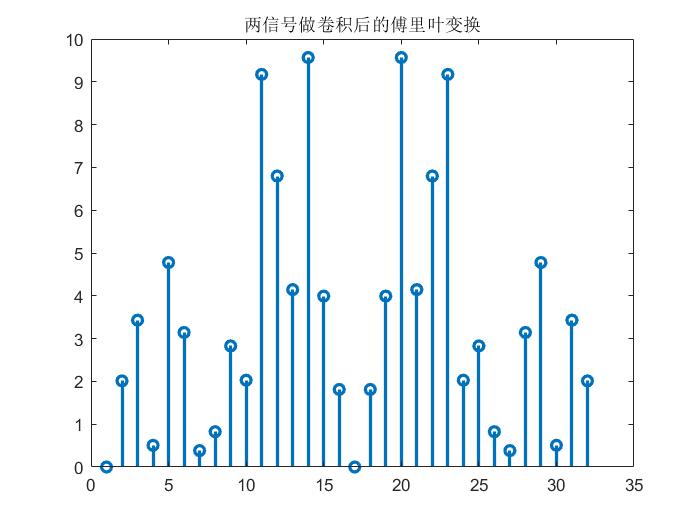
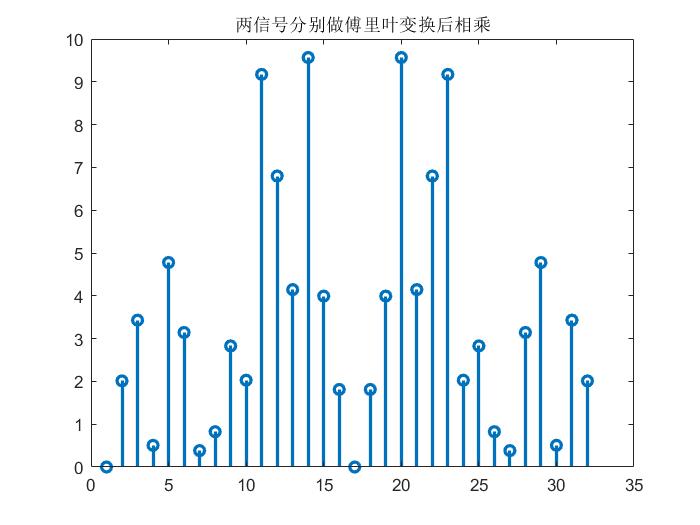
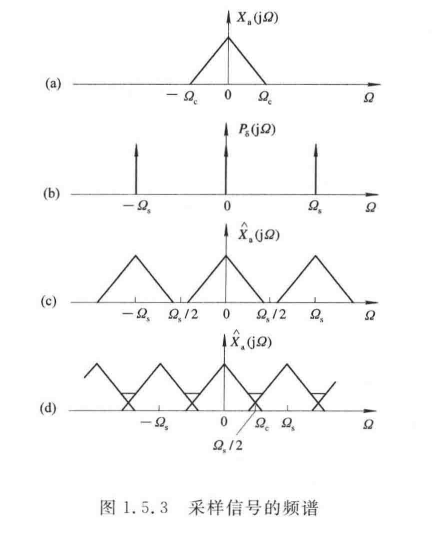
实际上，这种思想在验证采样信号的频谱时也得以体现：

quadquad 先分别求出原始模拟信号的傅里叶变换与冲激串的傅里叶变换，得到其频谱，再将两者相乘，便得到采样信号的频谱，与直接对采样信号进行傅里叶变换得到的频谱效果是一致的。

理想采样信号的频谱，是原模拟信号的频谱以采样角频率为周期，进行周期性延拓而成的。

且一个域的采样，必引起另一个域中的周期延拓。

最后

以上就是开心草丛最近收集整理的关于冲激信号的卷积性质&采样信号频谱的周期性延拓的全部内容，更多相关冲激信号内容请搜索靠谱客的其他文章。