系统稳定性判定（频域）

本文包含以下内容：
一、奈奎斯特稳定性判据
二、基于matlab对系统开环频率特性来判断系统稳定性

系统稳定性的简单理解可以移步 2021/03/09发的博文

一、奈奎斯特稳定性判据
$$Z=P-2N$$
其中，
Z为系统闭环传递函数右半平面极点数,当Z等于0,系统稳定;
P为开环传递函数右半平面极点个数；
N为系统开环奈奎斯特曲线包含（-1，j0）的圈数，逆时针为正；

改判据可以映射到对应的伯德图来进行，只是N的计量方式不同：
$$N＝（N＋）-（N－）$$
其中，
N＋为幅频曲线大于０时，对应相频曲线在频率增加方向,至下而上穿越-180°的次数;
N－为幅频曲线大于０时，对应相频曲线在频率增加方向,至上而下穿越-180°的次数;
特别注意,临界穿越点算0.5次.

二、基于matlab对系统开环频率特性来判断系统稳定性
假设开环传递函数为:
$$G(s)=\frac{K}{(s+2)(s^2+2s+5)}$$
我们来看不同K值下,系统的稳定性.
从开环传递函数可以看出,又半平面没有极点,P=0.
接下来我们通过matlab绘制不同K值下的奈奎斯特曲线,
输入以下代码:

den=[1 4 9 10];
for k = 10: 20: 100
    num = [k];
    nyquist(num, den);
    hold on
end

得到以下曲线:

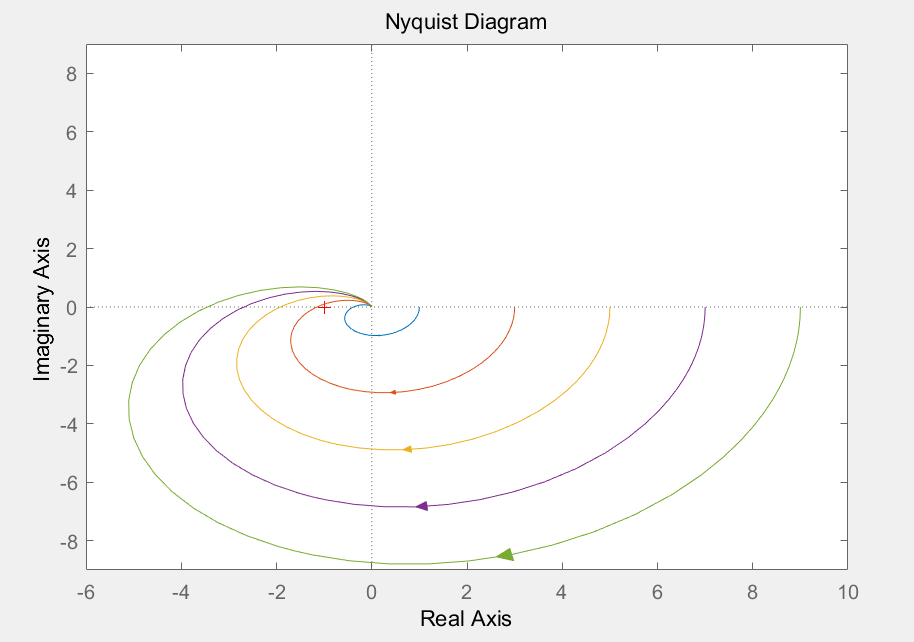
由图中可以得出,
当k=10时候,N等0,P=0,系统稳定
当k=30,50,70,90时,N等于-1,P=2,系统不稳定.

我们再用伯德图验证下,输入以下代码:

den=[1 4 9 10];
for k = 10: 20: 100
    num = [k];
    bode(num, den);
    hold on
end

得到以下图形:

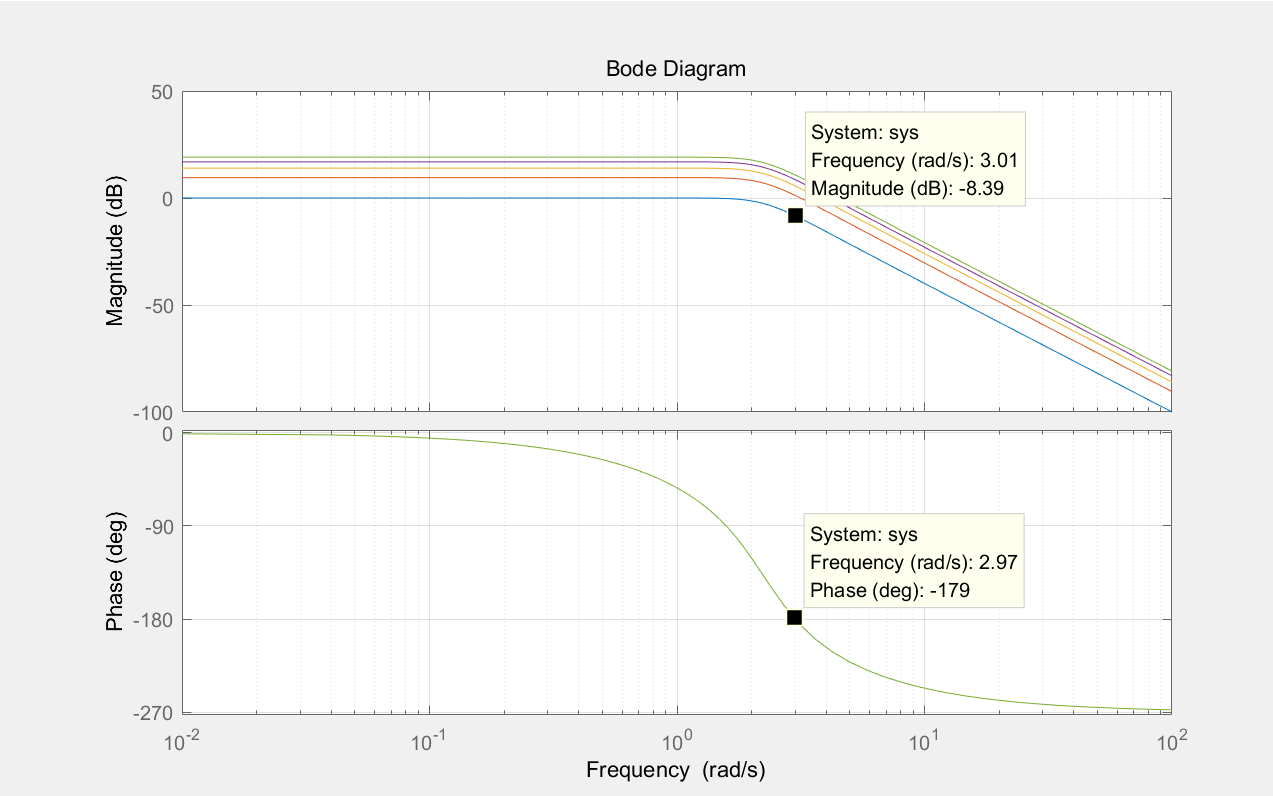
从图中而已看出
当k=10时候,N=0,P=0,系统稳定
当k=30,50,70,90时,N+=0,N-=1等于-1,P=2,系统不稳定.

用求根的方式再确认下k=30时的系统稳定性.
输入以下代码

num=[30];
den=[1 4 9 40];
roots(den)

ans =

  -4.1524 + 0.0000i
   0.0762 + 3.1028i
   0.0762 - 3.1028i

确实右半平面有两个根,系统不稳定.

最后

以上就是开心黑裤为你收集整理的系统稳定性判定（频域）的全部内容，希望文章能够帮你解决系统稳定性判定（频域）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。