奈奎斯特判据的个人理解

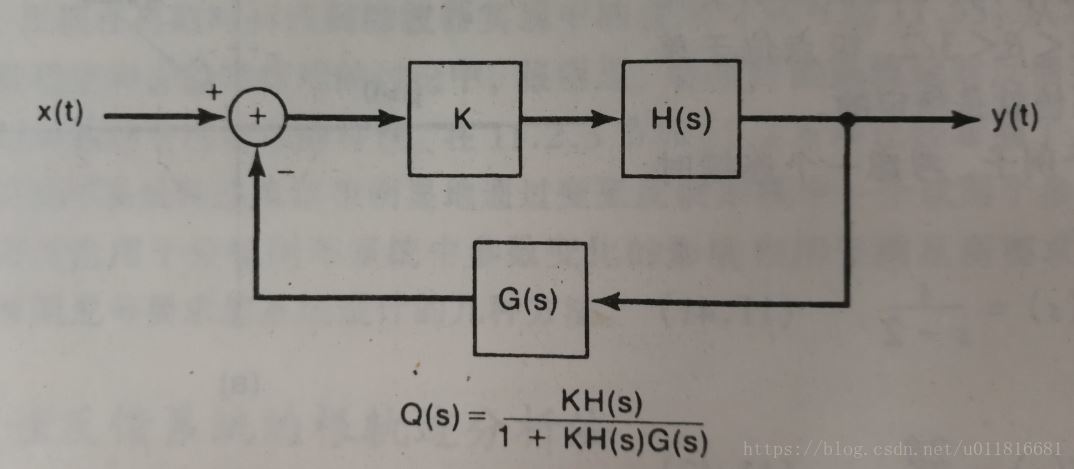
对于上述反馈系统而言，它的闭环传递函数为，它的开环传递函数为。我们期望这个反馈系统是稳定的，也就是说对于而言，我们希望它的极点都出现在平面的左半面。设辅助函数，这个函数等效于 的分母，因此的零点也就对应着的极点，的极点也就对应着的零点。所以我们期望稳定也就是希望的零点都出现在平面的左半面，或者说，平面的右半面没有的任何零点。那么我们如何判断在平面的右半面的零点个数呢？这就引入复变函数的围线性质。

围线性质

对于一个一般有理函数，其中是复变量。假设对复平面上一条沿顺时针闭合的围线求其所对应的，如下图所示。

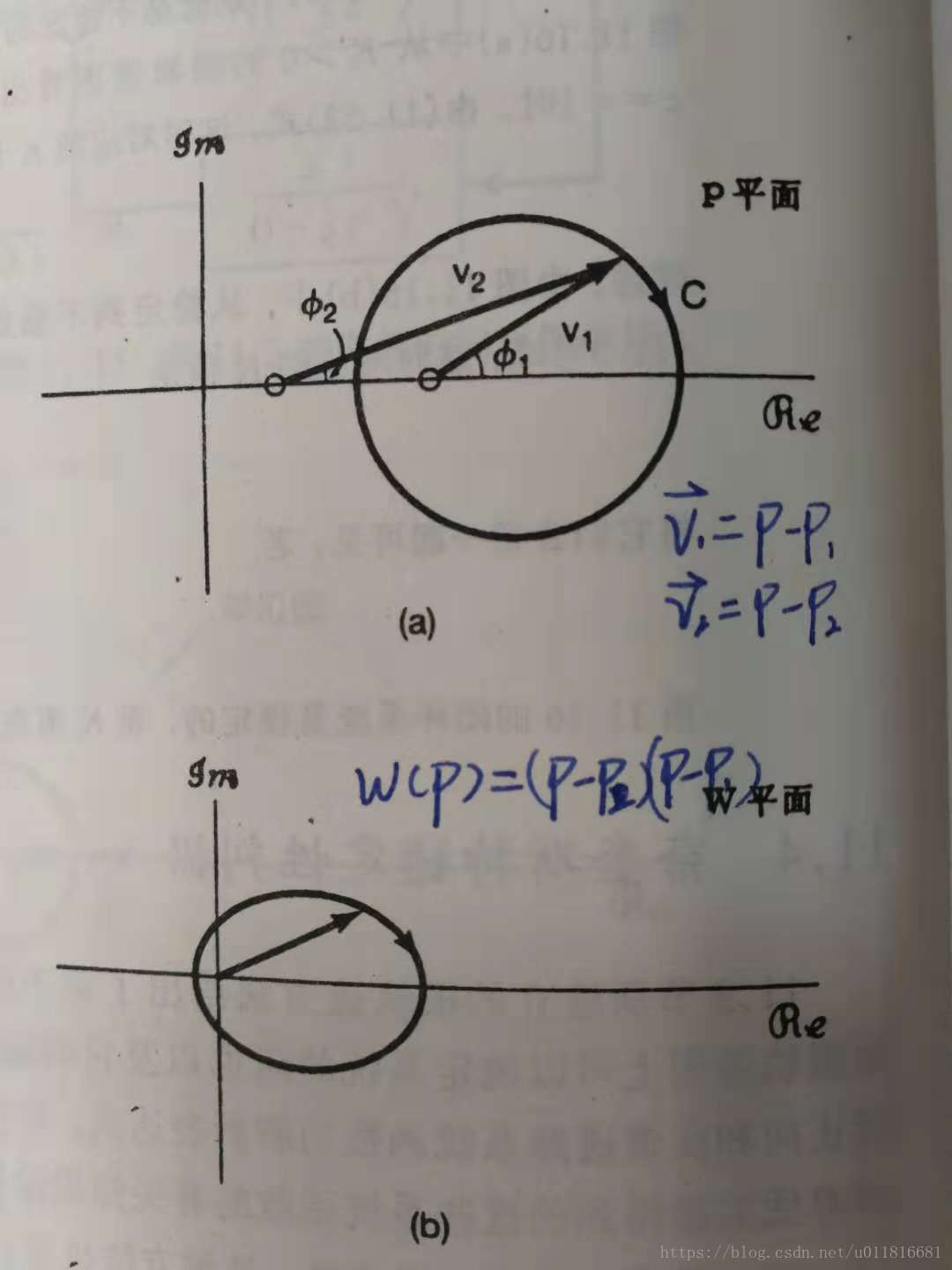
 这里为了方便说明，假设，也就是说这个函数存在两个零点，而没有任何极点。考虑复平面上的顺时针闭合围线包围了其中一个零点，那么随着围线上的点（复变量）顺时针旋转一周时，围线上的点与围线所包围的零点所形成的向量的相角变换，而围线上的点与围线外的零点所形成的向量的相角变换。因此对于有理函数而言，随着复平面上一条只包围一个零点的围线顺时针转一周，它的相角变换了，也就是说也在复平面上顺时针绕原点转了一周。

推展而言对于复平面上包围一个极点的顺时针围线而言，围线上的点与极点所形成的向量的相角变化也是，但是对于有理函数而言，随着复平面上一条只包围一个极点的围线顺时针转一周，它的相角变换了，也就是说也在复平面上逆时针绕原点转了一周。

由此得到复变函数的围线性质：当在平面内，以顺时针方向沿以闭合路径C绕一周时，对于沿这条闭和路径的值所对应的的图以顺时针方向环绕远点的净次数等于在平面上闭合路径C内的零点数减去它的极点数。

回到奈奎斯特判据

我们去s平面内一条囊括整个有伴平面的顺时针闭合围线C如下图所示。

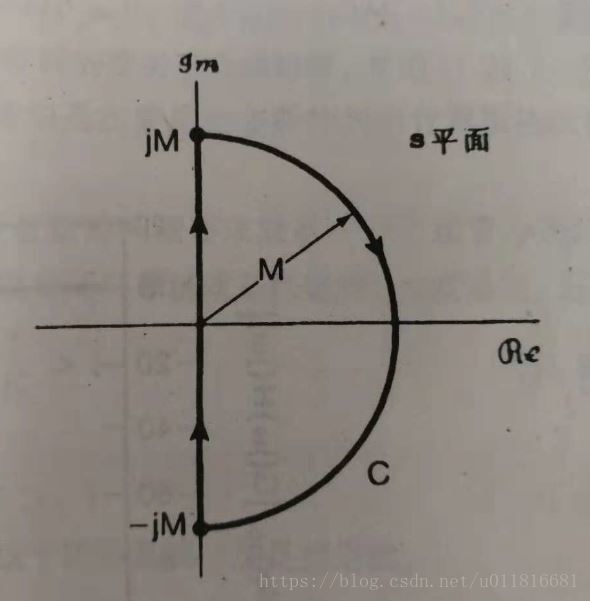
那么这个围线所对应的顺时针绕复平面上原点的圈数就等效于顺时针绕复平面上的圈数，这等于在s右半平面的零点数减去极点数。而在s右半平面的零点对应的就是闭环传递函数在s右半平面的极点，在s右半平面的极点对应的就是开环传递函数的极点。

综上所述，s平面内一条顺时针，囊括整个s右半平面的闭合围线C（如上图）所对应的开环传递函数在复平面上的曲线，顺时针绕复平面上的圈数，应该等于闭环传递函数在s右半平面的极点数减去开环传递函数的极点数。

为了使闭环传递函数稳定，那么就要求在s右半平面无任何极点，也就是说，

最后

以上就是平淡面包为你收集整理的奈奎斯特判据的个人理解的全部内容，希望文章能够帮你解决奈奎斯特判据的个人理解所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。