稳定判据_奈奎斯特稳定判据的简明通俗理解和应用

又到了大学春季学期，自控原理如期而至；还记得一年前我在学自控的时候，得到一位恩师的指导和解惑，问了老师太多自控原理的问题还去蹭现代控制理论，恩师都耐心解答，先在这里感谢恩师对我自控原理的指导和大学学习的“启蒙“。今天学直流电机运动控制的时候，回过头又翻看奈氏判据（幅相曲线和波德图判稳），再次感叹奈奎斯特判据的优美巧妙，并写下一些理解心得（没有很详细的每一步，只有难点的分析，故建议学到频域分析的时候再看帮助理解），希望对后面的同学有所帮助。

一、幅角原理

由自控原理教材（胡寿松版），奈奎斯特判稳的第一节是判据的数学基础——幅角原理；讲的是：复平面的一个复变函数F (s)=（s-z1）*（s-z2）/（s-p1）*（s-p2）（可以是任意的复变函数，这里用它方便讨论） ，然后它的自变量s进行顺时针运动，顺时针运动的轨迹是一个闭合轨迹（可以是圆或者任何闭合曲线）Γ曲线，且s运动的时候不能经过他的零极点（z1，z2和p1，p2），这个闭合轨迹包围的零极点个数P、Z和F(s) 绕坐标原点的圈数R有关，具体关系如下：R=P-Z。很抽象，请看下面的通俗分析：

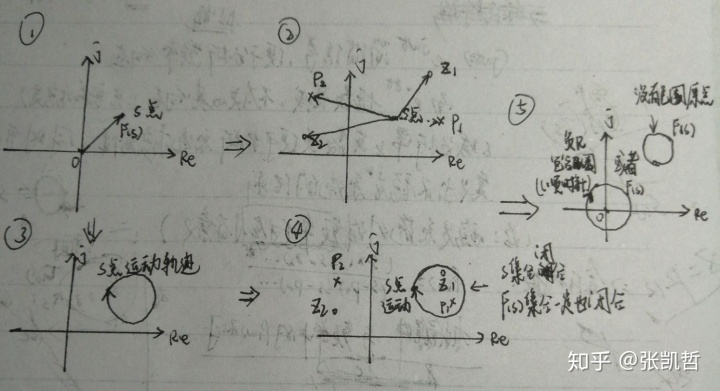
首先，任意一点s，它的F(s)的相角为 ∠F(S)=∠(s-z1) +∠(s-z2) -∠(s-p1) -∠(s-p2)，注意，∠F(S)对应的角度是对原点的夹角且我们这里不考虑长度（幅值），只考虑相角。

然后，如果这个任意一点s它运动起来，顺时针运动形成一个闭合曲线Γ，那么这个曲线如果包围了零点z1和极点p1，那么由复平面向量的相角定义，逆时针为正，顺时针为负，围绕闭合曲线Γ一周的角度为∫∠(s-z1)=∫∠(s-p1)＝-2π；而没有被包围的零点z2和极点p2所对应的角度∫∠(s-z2)=∫∠(s-p2)＝0。因此F(s)绕原点的圈数就与闭合曲线Γ包围零极点数有直接关系R=P-Z。（逆时针为正圈数，顺时针为负圈数）

二、复变函数F(s)和闭合曲线Γ的选择和频域转换

终于把第一步难关攻克，我们接下来看第二个问题，我们有了幅角原理，得到了F(s)绕原点的圈数就与闭合曲线Γ包围零极点数有直接关系R=P-Z，我们用它来做什么呢？

（1）构造需要的复变函数F(s)

令 F(s)=1+G(s)H(s)=1+B(s)/A(s)=[A(s)+B(s)]/A(s)，那么F(s)的极点为A(s)，也是开环传函的极点；F(s)的零点为A(s)+B(s)，是闭环传函的极点。不得不说，F(s)是非常巧妙的构造，F（s）联系开环传函和闭环传函；同时它的零点就是闭环传函的极点，正是我们判稳所需要的，即F(s)没有在s坐标实部大于0的极点，系统就是稳定的！

现在我们只知道开环传函G(s)H(s)，同时我们知道由教材不难理解F(s)绕原点的圈数就等价于开环传函绕（-1，0）的圈数。那么我们就可以用开环传函画圈，它绕（-1，0）的圈数就是F(s)绕原点的圈数——那我们就知道了R=P-Z中的R。由于开环传函已知，那么F(s)的极点就是开环传函的极点，它的位置我们也可以在s坐标具体确定，那么画出能确定R和P的闭合曲线Γ，我们也就能求出F(s)的Z=P-R,也就是被闭合曲线Γ包围的Z的个数。

（2）那么剩下的问题就是闭合曲线Γ到底怎么画呢？

第一步，想清楚我们是要干什么——判定稳定性，也就是Z（闭环极点数）在s坐标虚轴的右半平面个数为0。有了这个目标，那我们就知道要使闭合曲线Γ包围了整个虚轴右半平面，怎么用数学方法表达——s的实部从0到正无穷大，s的虚部从负无穷到正无穷；

第二步，闭合曲线Γ我们找好了，那么随之我们定下了P（开环极点被闭合曲线Γ包围的个数）。然后我们想知道R是多少？

第三步，我们如何通过确定了闭合曲线Γ，然后确定R【开环传函包围（-1，0）的圈数】呢？这是最美妙的一步，当我想通这一步的时候，我被奈奎斯特大师深深折服了！我们都知道，频域中的开环幅相曲线容易画，即jw从0到正无穷大（负无穷到0相当于对称的另一半）；而在s域，你却很难画出F(s)【或开环传函G(s)H(s)】在上述的闭合曲线Γ映射下的曲线到底包围原点【或(-1，0)点】多少圈。怎么办？前面的步骤都要前功尽弃了？当然不会，奈奎斯特大师给了我们答案——既然幅相曲线容易画出，那么我们能不能将s域转化为频域，忽略掉实部，我们就可以用幅相曲线得到R的值。我们知道一般情况下，开环传函的分子阶次都是小于分母的阶次，即s趋于无穷大时，开环传函的幅值是等于0的，也就是都收敛到了原点；而无穷大虚轴右半平面闭合曲线Γ又和虚轴有两个交点，故这个半圆闭合曲线Γ就可以等价到虚轴上（jw从负无穷到正无穷）。太妙了，s域就这么和频域jw等价了！

下面是我当时问我恩师同样的问题：

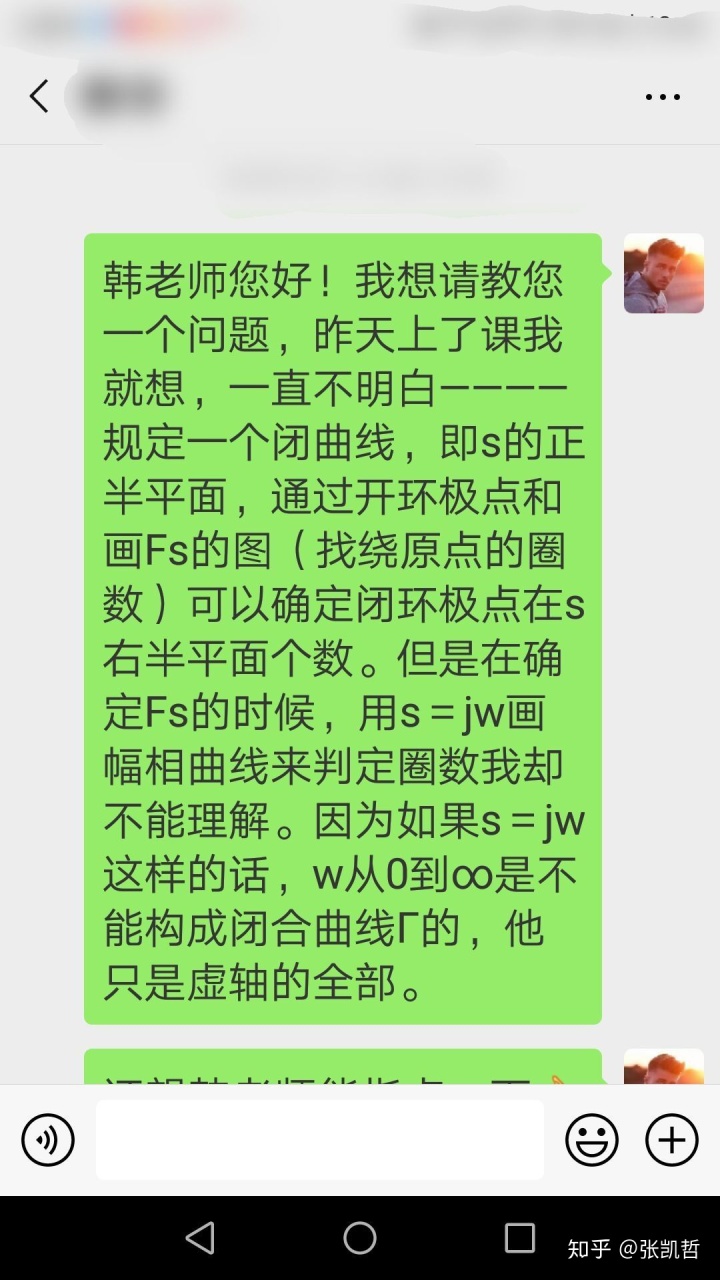
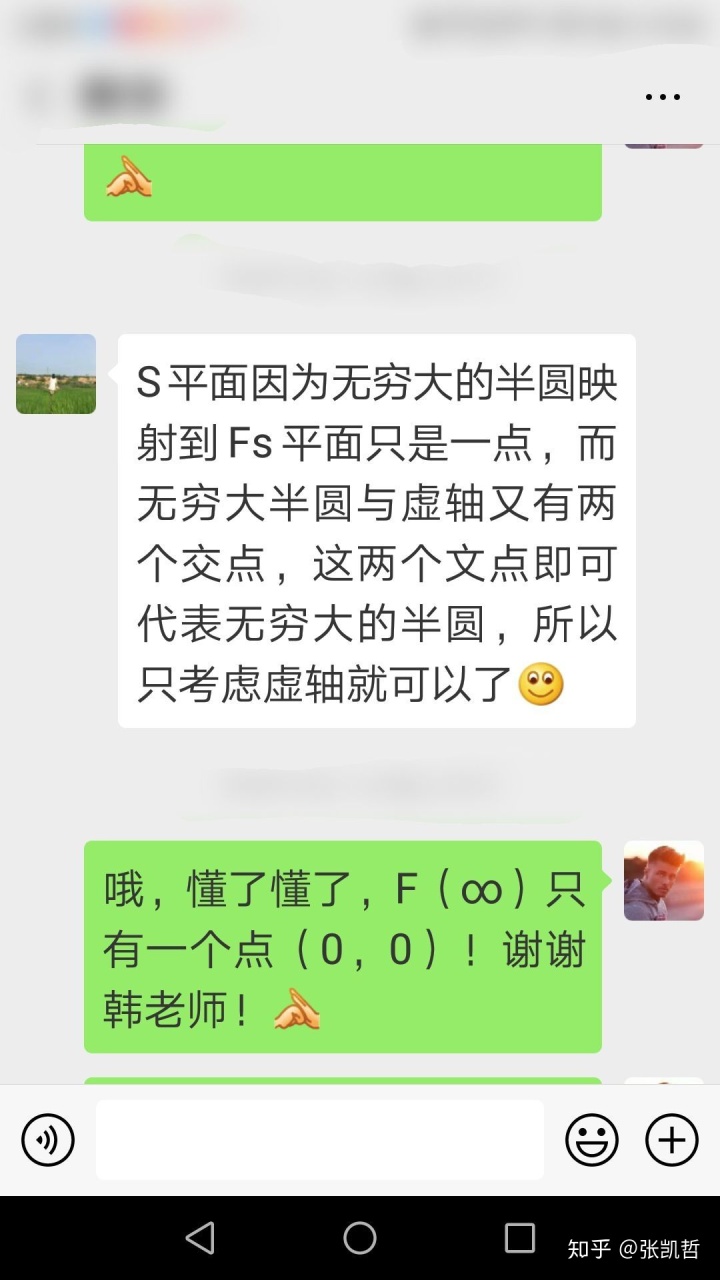
第四步，闭合曲线Γ已经等价到了整个虚轴，剩下就是用开环传函画幅相曲线，由于幅相曲线是jw从0到正无穷，即只含了一半的闭合曲线Γ。但是另一半是和实轴对称的，故求出的是与（-1，0）的半包围圈数，再乘2得到需要的R值。如果遇到积分环节或震荡环节，虚轴上会有开环极点，必须绕开，剩下具体的求法和注意点自控原理教材讲得很详细，我就不再赘述了。

三、奈奎斯特判据的应用

能坚持看到这里的电气控制系同学，很谢谢你们的耐心和信任！由于教材有频域分析的具体应用和设计，最后我只谈下自控原理频域分析和复频域分析的理解：

（1）复频域分析以根轨迹为主，同样是利用开环传递函数，根轨迹是研究根轨迹开环增益的变化导致闭环极点的走向。分析方便直观，清晰的说明了系统的稳态性能，但是对系统的动态性能设计却不是很好使。

（2）频域分析法的好处就比较多了，我个人认为频率是系统系统动态性能最直观的表达，可以通过波德图和幅相曲线判定稳定性和动态性能设计；而s域中加入衰减系数的实部，是一个指数衰减过程，它只起到判定稳定性（数学上就是收敛）的作用。当然，稳定性是系统的第一要求，如果没有稳定性，也就没有了频率响应和动态性能。

（3）时域是我们用来验证系统在频域中设计的好坏的，因为用它分析计算复杂，所以不用来设计。

（4）上述的判据都是基于经典控制理论的，即主要考虑的是系统的外特性，也就是分析输出响应，并没有解决系统内部变量的关系。在较低阶次或内部变量不多的对象中（如直流电机）还可以用波德图等频域分析设计，而面对内部变量较复杂的对象中（交流电机等）则需要用现代控制理论进行分析，学校一般会安排自控原理和现代控制一起上的。具体的分析我现在也在学，以后有机会继续交流。

（5）最后，控制理论不没有涉及到具体的对象，故有疑惑是正常的。但是系统传递函数结构清晰明了，方便我们打下理论基础，预祝每个同学都能学好自控原理！