信号与系统在仿真中的离散化

几种信号与系统里的典型环节传递函数

给定一个跃阶信号输入，各个系统的响应如下各图：
一阶惯性环节的微分方程：
$$T\dot{x}+x=y$$

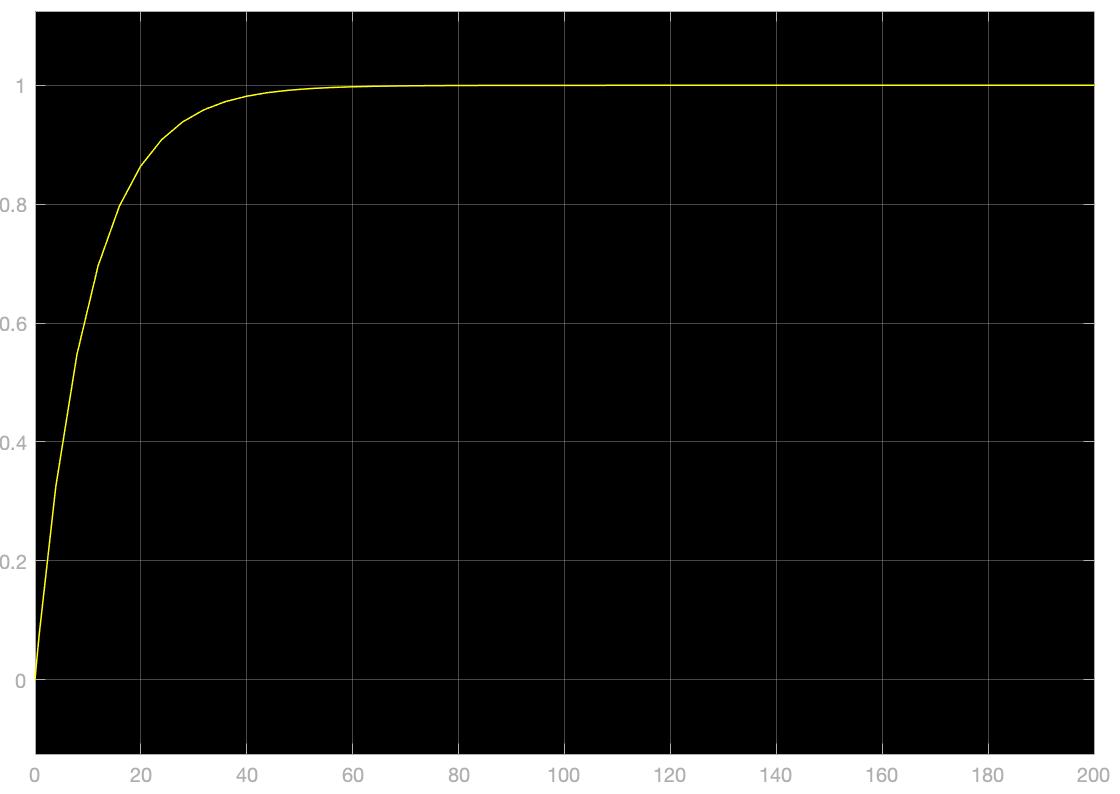
二阶惯性环节的微分方程：
$$T^2\ddot{x}+2\zeta T\dot{x}+x=y$$

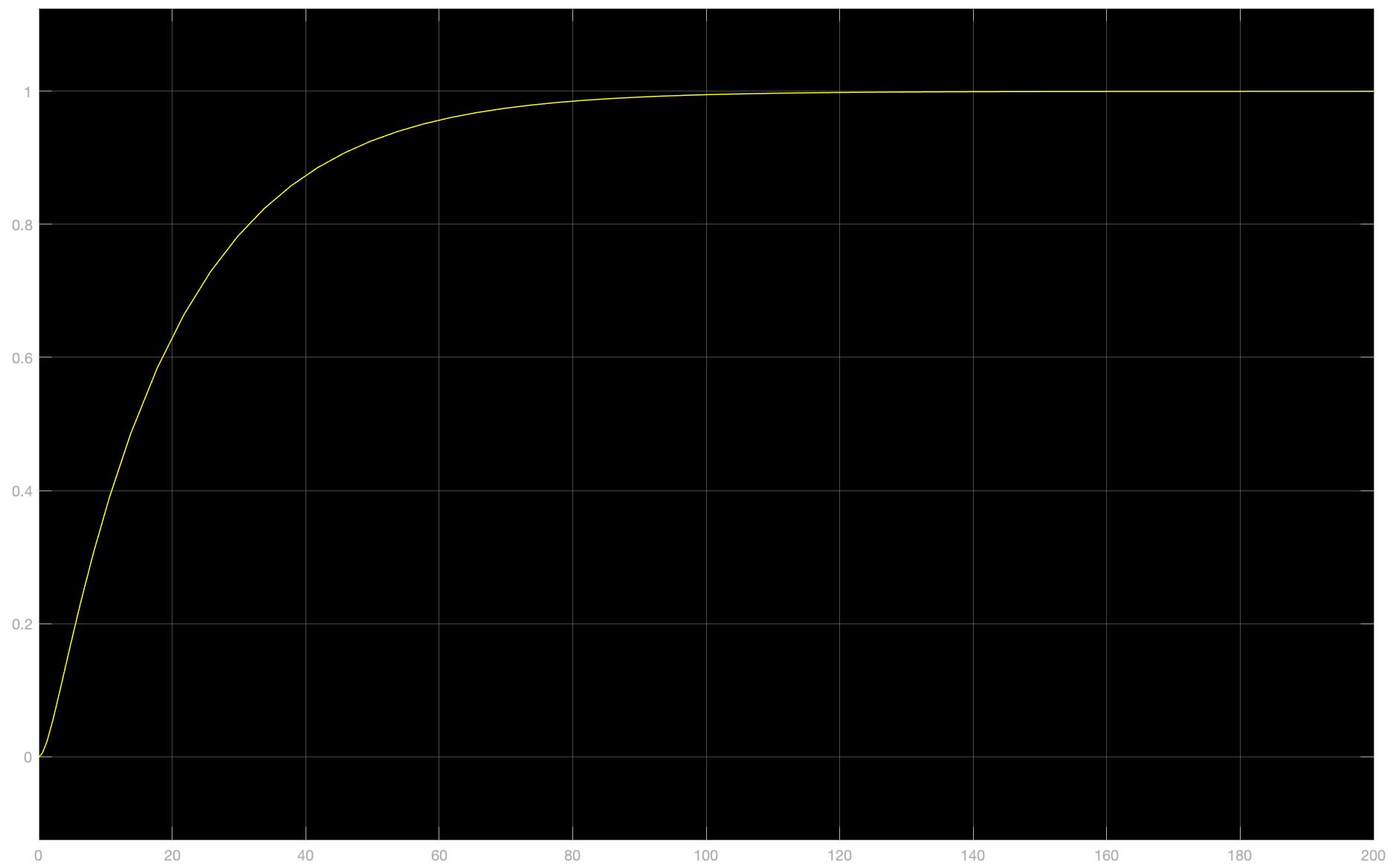
滞后环节的微分方程：
$$x(t-\tau )=y$$
滞后环节的图线是滞后一定时间的跃阶函数，这里就不画了。
一阶惯性环节的传递函数：
$$G(s)=\frac{1}{Ts+1}$$
二阶惯性环节的传递函数：
$$G(s)=\frac{1}{T^2{s}^2+2\zeta Ts+1}$$
滞后环节的传递函数：
$$G(s)=exp(-\tau s)$$

信号与系统中离散化的方法

Matlab中提供了五种离散连续信号的方法实现s域到z域的变换：

zoh零阶保持法；

foh一阶保持法；

tustin双线性变换法；

impulse脉冲响应法；

matched零极点匹配法。

根据z变换的理论，s域到z域最基本的映射关系是：
$$z=exp(Ts)$$
这种变化不会使频率发生畸变，但是会发生频率混叠现象，所以很少使用。实际计算中会对其进行简化处理，由连续信号传递函数转化得到近似的离散信号传递函数的模型。其中最简单的是由幂级数展开式的前两项进行变形得到关系式，用一阶后向差分的称为Euler法。
$$s=\frac{z-1}{T}$$
同样地，前向差分：
$$s=\frac{1-z}{T}$$
前向差分和后向差分法近似关系比较简单，而且不改变系统的稳态增益。但是前向差分可能改变系统的稳定性，并产生较大的畸变，一般不采用。后向差分不改变系统的稳定性，同样会产生畸变，但不存在频率混叠。

Tustin双线性变换法（matlab默认方法，也是主流的方法）：
$$s=\frac{2}{T}\frac{z-1}{z+1}$$
用梯形面积取代数值积分；特点和后向差分类似。但线性范围比后向差分要大。

零极点匹配法：
$$G(s)=\frac{K_s(s+z_1)(s+z_2)...}{(s+p_1)(s+p_2)(s+p_3)...}$$

$$G(z)=\frac{K_z(z-e^{-z_{1}T})(z-e^{-z_{2}T})...}{(z-e^{-p_{1}T})(z-e^{-p_{2}T})(z-e^{-p_{3}T})...}$$

映射关系为z变换，稳定性不变，频率混叠，没有畸变。

脉冲响应不变法和阶跃响应不变法（零阶保持器法）：

多对一变换，频率混叠；稳态增益改变（工程意义不大，不用于控制器设计）

零阶保持器：
$$G(s)=\frac{1-e^{-Ts}}{s}$$

$$X(z)=(1-z^{-1})\frac{z}{z-1}$$

一阶保持器：
$$G(s)=T(1+Ts)(\frac{1-e^{-Ts}}{Ts}{)}^2$$

离散化的差分方程

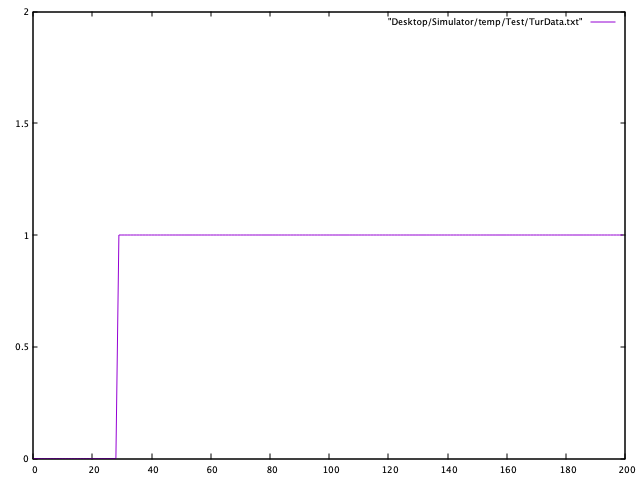
同样地我们使用跃阶函数作为输入，下面gnuplot画出的是用cpp代码输出的图线。
一阶惯性环节的差分方程：
$$y(k+1)=y(k)+\frac{\Delta t}{T}(x(k)-y(k))$$

//transfer function is G(s) = 1/(T*s+1)
double FirstOrderOscillation(double y_b,double x,double dt,double T){
    double y;
    y = y_b + dt/T * (x - y_b);
    return y;
}

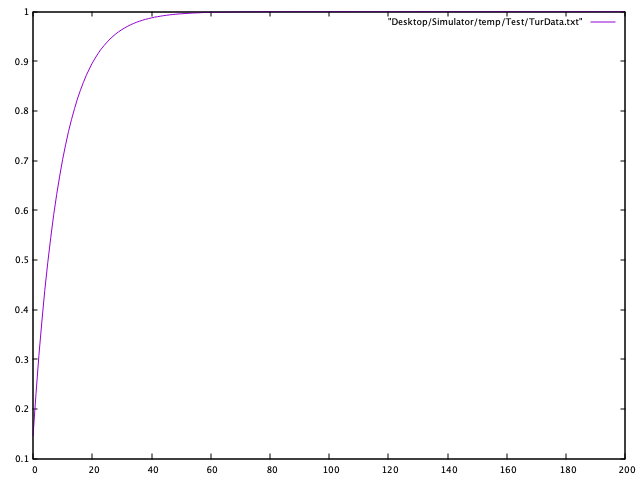
二阶惯性环节的差分方程：
$$y(k+2)=(2-\frac{2\zeta \Delta t}{T})y(k+1)+(\frac{2\zeta \Delta t}{T}-1-\frac{{\Delta t}^2}{T^2}y(k))+\frac{1}{T^2}x(k)$$

//transfer function is G(s) = 1/(Tˆ2*sˆ2+2*zeta*T*s+1)
double SecondOrderOscillation(double y_b,double y_bb,double x,double dt,double T,double zeta){
    double y;
    y = (2-2*zeta*dt/T)*y_b + (2*zeta*dt/T - 1 - dt*dt/(T*T))*y_bb + x/(T*T);
    return y;
}

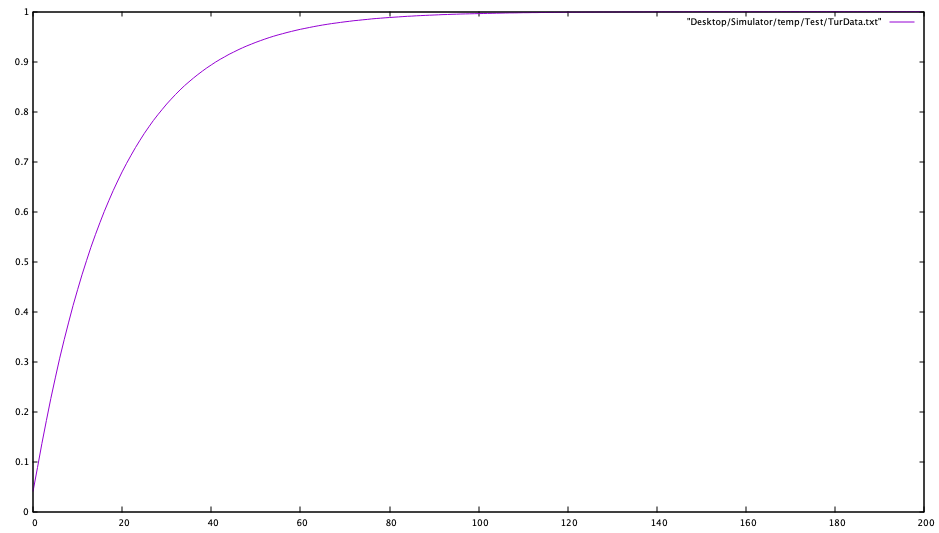
滞后环节差分方程：
$$y(k)=x(k-nT)$$

static std::vector<double> input_delay;
//transfer function is G(s) = exp(-tau*s)
double Delay(double tau,double x,double dt){
    double y;
    int delayedsteps = int(tau/dt);
    input_delay.insert(input_delay.begin(),x);
    if(input_delay.size() == uint64_t(delayedsteps)){
        y = input_delay.back();
        input_delay.pop_back();
        }
    else {
        y = 0.;
        }
    std::cout<<y<<std::endl;
    return y;
}

最后

以上就是醉熏刺猬为你收集整理的信号与系统在仿真中的离散化的全部内容，希望文章能够帮你解决信号与系统在仿真中的离散化所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。