MATLAB中tf函数的使用

目录

语法

说明

示例

SISO传递函数模型

离散时间SISO传递函数模型

阻尼比和固有频率的二阶传递函数

离散时间MIMO传递函数模型

将SISO传递函数连接到MIMO传递函数模型中

使用有理表达式的传递函数模型

使用有理表达式的离散时间传递函数模型

具有继承属性的传递函数模型

传递函数模型阵列

将状态空间模型转换为传递函数

        使用tf创建实值或复值传递函数模型，或转换动态系统模型传递函数形式。传递函数是线性时不变系统的频域表示。例如，考虑由传递函数表示的连续时间SISO动态系统sys(s) = N(s)/D(s)，在哪里s = jw和N(s)和D(s)分别称为分子多项式和分母多项式。这tf模型对象可以表示连续时间或离散时间中SISO或MIMO传递函数。可以通过直接指定其系数或通过转换另一种类型的模型(如状态空间模型)来创建传递函数模型对象ss)转换成传递函数形式。也可以使用tf为了创建广义状态空间(genss)模型或不确定状态空间(uss(鲁棒控制工具箱))模特。

语法

sys = tf(numerator,denominator)
sys = tf(numerator,denominator,ts)
sys = tf(numerator,denominator,ltiSys)
sys = tf(m)
sys = tf(___,Name,Value)
sys = tf(ltiSys)
sys = tf(ltiSys,component)
s = tf('s')
z = tf('z',ts)

说明

sys = tf(numerator,denominator)创建连续时间传递函数模型，设置Numerator和Denominator属性。例如，考虑由传递函数表示的连续时间SISO动态系统sys(s) = N(s)/D(s)，输入参数numerator和denominator是的系数分别为N(s)和D(s)。

sys = tf(numerator,denominator,ts)创建离散时间传递函数模型，设置Numerator, Denominator，以及Ts属性。例如，考虑由传递函数表示的离散时间SISO动态系统sys(z) = N(z)/D(z)，输入参数numerator和denominator是的系数分别为N(z)和D(z)。若要不指定采样时间，请设置ts的输入参数-1.

sys = tf(numerator,denominator,ltiSys)使用从动态系统模型继承的属性创建传递函数模型ltiSys，包括采样时间。

sys = tf(m)创建表示静态增益的传递函数模型，m.

sys = tf(___,Name,Value)使用一个或多个设置传递函数模型的属性Name,Value为任何先前的输入参数组合配对参数。

sys = tf(ltiSys)转换动态系统模型ltiSys传递函数模型。

sys = tf(ltiSys,component)转换指定的component关于ltiSys传递函数形式。仅在以下情况下使用此语法ltiSys是已识别的线性时不变(LTI)模型。

s = tf('s')创建特殊变量s您可以在rational表达式中使用它来创建连续时间传递函数模型。使用有理表达式有时比指定多项式系数更容易、更直观。

z = tf('z',ts)创建特殊变量z可以在rational表达式中使用它来创建离散时间传递函数模型。若要不指定采样时间，请设置ts的输入参数-1.

示例

SISO传递函数模型

        对于这个例子，考虑下面的SISO传递函数模型:

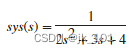
        指定按降序排列的分子和分母系数s，并创建传递函数模型。 

numerator = 1;
denominator = [2,3,4];
sys = tf(numerator,denominator)

%%
sys =
 
         1
  ---------------
  2 s^2 + 3 s + 4

离散时间SISO传递函数模型

        对于这个例子，考虑下面的离散时间SISO传递函数模型:

        指定按降序排列的分子和分母系数z和0.1秒的采样时间。创建离散时间传递函数模型。 

numerator = [2,0];
denominator = [4,0,3,-1];
ts = 0.1;
sys = tf(numerator,denominator,ts)

%%
sys =
 
        2 z
  ---------------
  4 z^3 + 3 z - 1
 

阻尼比和固有频率的二阶传递函数

        对于本例，考虑一个传递函数模型，它代表一个具有已知固有频率和阻尼比的二阶系统。

        用阻尼比表示的二阶系统的传递函数ζ和自然频率ω0，是:

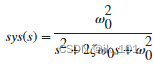
        假设一个阻尼比，ζ= 0.25和固有频率，ω0= 3弧度/秒，创建二阶传递函数。 

zeta = 0.25;
w0 = 3;
numerator = w0^2;
denominator = [1,2*zeta*w0,w0^2];
sys = tf(numerator,denominator)

%%
sys =
 
         9
  ---------------
  s^2 + 1.5 s + 9

        检查该传递函数对阶跃输入的响应。

stepplot(sys)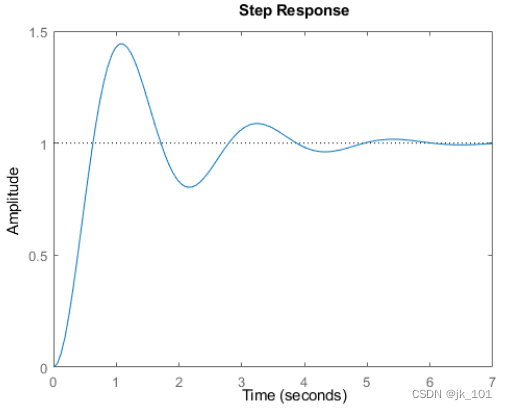

        该图显示了低阻尼比二阶系统的预期衰荡。

离散时间MIMO传递函数模型

        创建离散时间、多输入、多输出模型的传递函数:

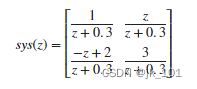
        带采样时间ts = 0.2秒。将分子系数指定为2乘2矩阵。

numerators = {1 [1 0];[-1 2] 3};

        将公分母的系数指定为行向量。

denominator = [1 0.3];

        创建离散时间MIMO传递函数模型。

ts = 0.2;
sys = tf(numerators,denominator,ts)


sys =
 
  From input 1 to output...
          1
   1:  -------
       z + 0.3
 
       -z + 2
   2:  -------
       z + 0.3
 
  From input 2 to output...
          z
   1:  -------
       z + 0.3
 
          3
   2:  -------
       z + 0.3

将SISO传递函数连接到MIMO传递函数模型中

        在本例中，通过串联SISO传递函数模型来创建MIMO传递函数模型。考虑以下单输入、双输出传递函数:

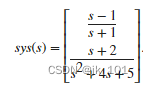
        通过连接SISO条目来指定MIMO传递函数模型。 

sys1 = tf([1 -1],[1 1]);		
sys2 = tf([1 2],[1 4 5]);
sys = [sys1;sys2]


sys =
 
  From input to output...
       s - 1
   1:  -----
       s + 1
 
           s + 2
   2:  -------------
       s^2 + 4 s + 5
 

使用有理表达式的传递函数模型

        对于这个例子，使用有理表达式创建一个连续时间传递函数模型。使用有理表达式有时比指定分子和分母的多项式系数更容易和更直观。

        考虑以下系统:

        要创建传递函数模型，首先指定s作为一个tf对象。

s = tf('s')


s =
 
  s
 

        使用有理表达式中的s创建传递函数模型。

sys = s/(s^2 + 2*s + 10)


sys =
 
        s
  --------------
  s^2 + 2 s + 10
 

使用有理表达式的离散时间传递函数模型

        对于这个例子，使用一个有理表达式创建一个离散时间传递函数模型。使用有理表达式有时比指定多项式系数更容易、更直观。

        考虑以下系统:

        要创建传递函数模型，首先指定z作为一个tf对象和采样时间Ts. 

ts = 0.1;
z = tf('z',ts)


z =
 
  z

        使用以下公式创建传递函数模型z在理性的表达中。

sys = (z - 1) / (z^2 - 1.85*z + 0.9)


sys =
 
        z - 1
  ------------------
  z^2 - 1.85 z + 0.9

具有继承属性的传递函数模型

        对于本例，创建一个传递函数模型，其属性继承自另一个传递函数模型。考虑以下两个传递函数:

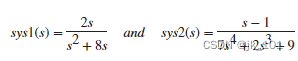
        对于本例，创建sys1与TimeUnit和InputDelay属性设置为'minutes'.

numerator1 = [2,0];
denominator1 = [1,8,0];
sys1 = tf(numerator1,denominator1,'TimeUnit','minutes','InputUnit','minutes')


sys1 =
 
     2 s
  ---------
  s^2 + 8 s


%%
propValues1 = [sys1.TimeUnit,sys1.InputUnit]
propValues1 = 1x2 cell
    {'minutes'}    {'minutes'}

        使用从继承的属性创建第二个传递函数模型sys1.

numerator2 = [1,-1];
denominator2 = [7,2,0,0,9];
sys2 = tf(numerator2,denominator2,sys1)


sys2 =
 
        s - 1
  -----------------
  7 s^4 + 2 s^3 + 9



%%
propValues2 = [sys2.TimeUnit,sys2.InputUnit]
propValues2 = 1x2 cell
    {'minutes'}    {'minutes'}
 

        观察传递函数模型sys2具有与...相同属性sys1.

传递函数模型阵列

        可以使用for循环来指定传递函数模型的数组。首先，用零预先分配传递函数数组。

sys = tf(zeros(1,1,3));

        前两个指数表示模型的输出和输入的数量，而第三个指数是阵列中模型的数量。使用中的有理表达式创建传递函数模型数组for循环。

s = tf('s');                                                  
for k = 1:3                                                             
    sys(:,:,k) = k/(s^2+s+k);                                          
end
sys


sys(:,:,1,1) =
 
       1
  -----------
  s^2 + s + 1
 

sys(:,:,2,1) =
 
       2
  -----------
  s^2 + s + 2
 

sys(:,:,3,1) =
 
       3
  -----------
  s^2 + s + 3

将状态空间模型转换为传递函数

        对于本例，计算以下状态空间模型的传递函数:

使用状态空间矩阵创建状态空间模型。

A = [-2 -1;1 -2];
B = [1 1;2 -1];
C = [1 0];
D = [0 1];
ltiSys = ss(A,B,C,D);

        转换状态空间模型ltiSys一个传递函数。

sys = tf(ltiSys)

sys =
 
  From input 1 to output:
        s
  -------------
  s^2 + 4 s + 5
 
  From input 2 to output:
  s^2 + 5 s + 8
  -------------
  s^2 + 4 s + 5

最后

以上就是甜美小笼包为你收集整理的MATLAB中tf函数的使用的全部内容，希望文章能够帮你解决MATLAB中tf函数的使用所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。