目录
- 1.题目一
- 2.题目二
- 3.题目三
- 4.题目四
1.题目一
编写MATLAB程序,求以下各序列的z变换:
使用ztrans求解,得到结果如下:
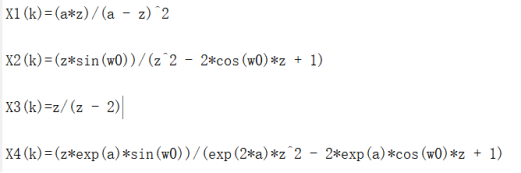
使用自建函数symdisp,使结果以数学公式表示:
syms n a w0
x1 = n*a^n;
X1 = ztrans(x1);%求x1(n)的Z变换
x2 = sin(w0*n);
X2 = ztrans(x2);%求x2(n)的Z变换
x3 = 2^n;
X3 = ztrans(x3);%求x3(n)的Z变换
x4 = exp(-a*n)*sin(w0*n);
X4 = ztrans(x4);%求x4(n)的Z变换
fprintf('X1(k)=')
disp(X1);
fprintf('X2(k)=')
disp(X2);
fprintf('X3(k)=')
disp(X3);
fprintf('X4(k)=')
disp(X4);
% %需要添加symdisp函数后才可运行
% symdisp(X1);%以直观的数学公式显示
% symdisp(X2);
% symdisp(X3);
% symdisp(X4);
symdisp.m
function h=symdisp(s)
%//SYMDISP Display a symbolic expression in human readable form.
%// symdisplay(S) displays the symbolic expression S in a small figure window,
%// using standard mathematical notation.
%//
%// Examples:
%// syms x t positive
%// f=taylor(cos(x));
%// symdisp(f)
%// f=int(exp(-t)*t^(x-1),t,0,inf);
%// symdisp(f)
%//
%// Required toolbox: Symbolic Math
%//
%// See also SYMBOLIC PRETTY.
if ~isa(s,'sym')
s=sym(s);
%error('输入参数必须是sym类型,请使用 sym() 将你的结果转化为sym类型.')
end
S=['$',latex(s),'$'];
S=strrep(S,'&','& quad');
S=strrep(S,'{it','mathrm{');
h=msgbox(S,'字符的数学展示形式');
h1=get(h,'children');
h2=h1(1);
h3=get(h2,'children');
if isempty(h3)
h2=h1(2); h3=get(h2,'children');
end
set(h3,'visible','off')
set(h3,'interpreter','latex')
set(h3,'string',S)
set(h3,'fontsize',20)
w=get(h3,'extent');
W=get(h,'position');
W(3)=max(w(3)+10,125);
W(4)=w(4)+40;
set(h,'position',W)
h4=h1(2);
if ~strcmp(get(h4,'tag'),'OKButton'), h4=h1(1); end
o=get(h4,'position');
o(1)=(W(3)-o(3))/2;
set(h4,'position',o)
set(h3,'visible','on')
set(h,'color','w');
2.题目二
编写MATLAB程序,用部分分式法求解下列系统的z反变换,写出x(n)的表示式,并用图形与impz求得的结果相比较,取前10个点作图
使用部分分式法求解Z反变换,得到第一个X(z)的多项式分解结果:
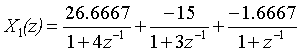
得到x1(n)的表达式为(假设为因果序列):
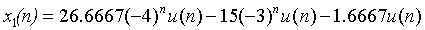
得到第二个X(z)的多项式分解结果:
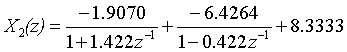
得到x2(n)的表达式为(假设为因果序列):
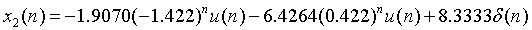
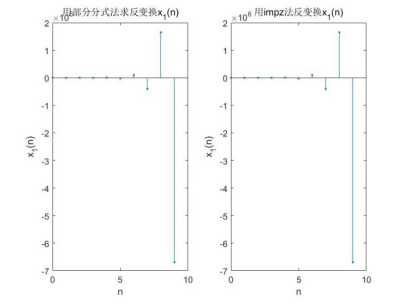
对第一个X(z)使用部分分式法和impz法分别求解Z反变换,图形如下:
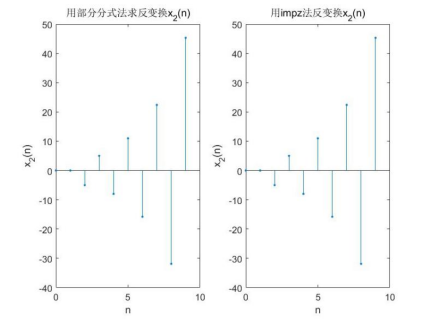
对第二个X(z)使用部分分式法和impz法分别求解Z反变换,图形如下:
N=10;
n=0:N-1;
b1=[10,20,0,0];
a1=[1,8,19,12];
[r1,p1,c1] = residuez(b1,a1); %将有理多项式部分分式展开
x1=r1(1)*p1(1).^n+r1(2)*p1(2).^n+r1(3)*p1(3).^n; %求X1(Z)的反变换x1(n)
x1_1=impz(b1,a1,N); %使用impz求解
figure;subplot(1,2,1);stem(n,x1,'.');
title('用部分分式法求反变换x_1(n)');
xlabel('n');ylabel('x_1(n)');
subplot(1,2,2);stem(n,x1_1,'.');
title('用impz法反变换x_1(n)');
xlabel('n');ylabel('x_1(n)')
b2=[0,0,-5];
a2=[1,1,-0.6];
[r2,p2,c2] = residuez(b2,a2); %将有理多项式部分分式展开
x2=r2(1)*p2(1).^n+r2(2)*p2(2).^n+c2(1).*(n==0); %求X2(Z)的反变换x2(n)
x2_1=impz(b2,a2,N); %使用impz求解
figure;subplot(1,2,1);stem(n,x2,'.');
title('用部分分式法求反变换x_2(n)');
xlabel('n');ylabel('x_2(n)');
subplot(1,2,2);stem(n,x2_1,'.');
title('用impz法反变换x_2(n)');
xlabel('n');ylabel('x_2(n)')、
3.题目三
编写MATLAB程序,已知离散时间系统的传递函数(tf)模型:
要求将其转换为:
①零-极点增益(zpk)模型;②二次分式(sos)模型;③极点留数(rpk)模型;④状态变量(ss)模型。
①使用tf2zpk求得zpk模型为:

即零-极点增益模型的系统函数为:
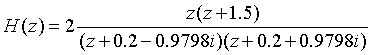
②使用tf2sos求得sos模型为:
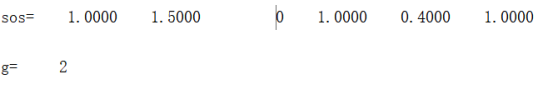
即二次分式模型如下:
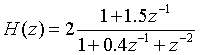
③使用residuez求得rpk模型为:

即极点留数模型为:
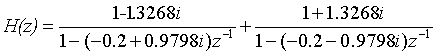
④使用tf2ss求得ss模型为:

将这些系数代入状态方程中即可得到系统的状态方程。
num=[2,3,0]; %tf模型中分子多项式的系数向量
den=[1,0.4,1]; %tf模型中分母多项式的系数向量
[z,p,k]=tf2zp(num,den);%将tf模型转换为zpk模型
[sos,g]=tf2sos(num,den);%将tf模型转换为sos模型
[r1,p1,k1]=residuez(num,den);%将tf模型转换为rpk模型
[A,B,C,D]=tf2ss(num,den);%将tf模型转换为ss模型
fprintf('z=')
disp(z);
fprintf('p=')
disp(p);
fprintf('k=')
disp(k);
fprintf('sos=')
disp(sos);
fprintf('g=')
disp(g);
fprintf('r=')
disp(r1);
fprintf('p=')
disp(p1);
fprintf('k=')
disp(k1);
fprintf('A=')
disp(A);
fprintf('B=')
disp(B);
fprintf('C=')
disp(C);
fprintf('D=')
disp(D);
4.题目四
4.已知离散时间系统的零-极点增益(zpk)模型为:
要求将其转换为:①传递函数(tf)模型;②二次分式(sos)模型;③极点留数(rpk)模型。
①使用zp2tf求得tf模型为:
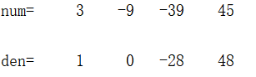
即系统传递函数模型为:
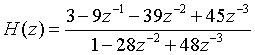
②使用zp2sos求得sos模型为:

即二次分式模型为:
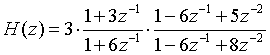
③使用residuez求得rpk模型为:

即极点留数模型为:
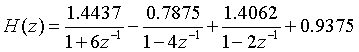
z=[1,-3,5]';
p=[2,4,-6]';
k=3;
[num,den]=zp2tf(z,p,k);%将zpk模型转换为tf模型
[sos,g]=zp2sos(z,p,k);%将zpk模型转换为sos模型
[r1,p1,k1]=residuez(num,den);%将zpk模型转换为rpk模型
fprintf('num=')
disp(num);
fprintf('den=')
disp(den);
fprintf('sos=n')
disp(sos);
fprintf('g=')
disp(g);
fprintf('r=n')
disp(r1);
fprintf('p=n')
disp(p1);
fprintf('k=')
disp(k1);
最后
以上就是快乐大碗最近收集整理的关于数字信号处理实验41.题目一2.题目二3.题目三4.题目四的全部内容,更多相关数字信号处理实验41内容请搜索靠谱客的其他文章。
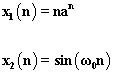
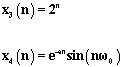
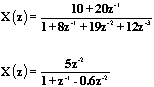
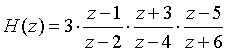








发表评论 取消回复