此系列属于胡寿松《自动控制原理题海与考研指导》(第三版)习题精选,仅包含部分经典习题,需要完整版习题答案请自行查找,本系列属于知识点巩固部分,搭配如下几个系列进行学习,可用于期末考试和考研复习。
自动控制原理(第七版)知识提炼
自动控制原理(第七版)课后习题精选
自动控制原理(第七版)附录MATLAB基础
第六章:线性系统的校正方法
Example 6.1
设单位反馈的开环传递函数为: G 0 ( s ) = K s ( s + 1 ) ( 0.5 s + 1 ) G_0(s)=displaystylefrac{K}{s(s+1)(0.5s+1)} G0(s)=s(s+1)(0.5s+1)K,要求设计一串联校正网络,使校正后系统的开环增益 K = 5 K=5 K=5,相角裕度不低于 40 ° 40° 40°,幅值裕度不小于 10 d B 10{rm dB} 10dB.
解:
由题意可得,取
K
=
5
K=5
K=5,则待校正系统的传递函数为:
G
0
(
s
)
=
5
s
(
s
+
1
)
(
0.5
s
+
1
)
G_0(s)=frac{5}{s(s+1)(0.5s+1)}
G0(s)=s(s+1)(0.5s+1)5
-
绘制待校正系统的对数幅频渐近特性曲线。
待校正系统的对数幅频渐近特性曲线如下图 L ′ ( ω ) L'(omega) L′(ω)所示.由图可知,待校正系统的截止频率为: ω c ′ = 2.15 r a d / s omega_c'=2.15{rm rad/s} ωc′=2.15rad/s,计算待校正系统的相角裕度。
γ ′ = 180 ° − 90 ° − ( arctan ω c ′ + arctan 0.5 ω c ′ ) ∣ ω c ′ = 2.15 = − 22.13 ° gamma'=left.180°-90°-(arctanomega_c'+arctan0.5omega_c')right|_{omega_c'=2.15}=-22.13° γ′=180°−90°−(arctanωc′+arctan0.5ωc′)∣ωc′=2.15=−22.13°
表明待校正系统不稳定.由于
φ m = γ − γ ′ = 40 ° + 22.13 ° = 62.13 ° > 60 ° varphi_m=gamma-gamma'=40°+22.13°=62.13°>60° φm=γ−γ′=40°+22.13°=62.13°>60°
故考虑采用串联滞后校正. -
由要求的 γ ′ ′ gamma'' γ′′选择 ω c ′ ′ omega_c'' ωc′′。
选取 φ ( ω c ′ ′ ) = − 6 ° varphi(omega_c'')=-6° φ(ωc′′)=−6°,要求 γ ′ ′ = 40 ° gamma''=40° γ′′=40°,有: γ ′ ( ω c ′ ′ ) = γ ′ ′ − φ ( ω c ′ ′ ) = 46 ° gamma'(omega_c'')=gamma''-varphi(omega_c'')=46° γ′(ωc′′)=γ′′−φ(ωc′′)=46°.
由 γ ′ = 90 ° − arctan ω c ′ ′ − arctan 0.5 ω c ′ ′ gamma'=90°-arctanomega_c''-arctan0.5omega_c'' γ′=90°−arctanωc′′−arctan0.5ωc′′,解得已校正系统的截止频率: ω c ′ ′ = 0.54 r a d / s omega_c''=0.54{rm rad/s} ωc′′=0.54rad/s.
-
确定滞后网络参数 b b b和 T T T.
当 ω c ′ ′ = 0.54 r a d / s omega_c''=0.54{rm rad/s} ωc′′=0.54rad/s时,由图可测得: L ′ ( ω c ′ ′ ) = 19.33 d B L'(omega_c'')=19.33{rm dB} L′(ωc′′)=19.33dB;
由 20 lg b = − L ′ ( ω c ′ ′ ) 20lg{b}=-L'(omega_c'') 20lgb=−L′(ωc′′),解得: b = 0.11 b=0.11 b=0.11。
令 1 b T = 0.1 ω c ′ ′ displaystylefrac{1}{bT}=0.1omega_c'' bT1=0.1ωc′′,解得: T = 168.35 T=168.35 T=168.35。
则有串联滞后校正网络对数幅频渐近特性曲线如下图 L c ( ω ) L_c(omega) Lc(ω)所示,其传递函数为:
G c ( s ) = 1 + b T s 1 + T s = 1 + 18.52 s 1 + 168.35 s G_c(s)=frac{1+bTs}{1+Ts}=frac{1+18.52s}{1+168.35s} Gc(s)=1+Ts1+bTs=1+168.35s1+18.52s
已校正系统的对数幅频渐近特性曲线如下图 L ′ ′ ( ω ) L''(omega) L′′(ω)所示,其传递函数为:
G c ( s ) G 0 ( s ) = 5 ( 18.52 s + 1 ) s ( s + 1 ) ( 0.5 s + 1 ) ( 168.35 s + 1 ) G_c(s)G_0(s)=frac{5(18.52s+1)}{s(s+1)(0.5s+1)(168.35s+1)} Gc(s)G0(s)=s(s+1)(0.5s+1)(168.35s+1)5(18.52s+1) -
验算性能指标。
γ ′ ′ = 180 ° + ∠ G c ( j ω c ′ ′ ) G 0 ( j ω c ′ ′ ) = 90 ° + ( arctan 18.52 ω c ′ ′ − arctan ω c ′ ′ − arctan 0.5 ω c ′ ′ − arctan 168.35 ω c ′ ′ ) ∣ ω c ′ ′ = 0.54 = 41.44 ° > 40 ° begin{aligned} gamma''&=180°+angle{G_c({rm j}omega_c'')G_0({rm j}omega_c'')}\\ &=left.90°+(arctan18.52omega_c''-arctanomega_c''-arctan0.5omega_c''-arctan168.35omega_c'')right|_{omega_c''=0.54}=41.44°>40° end{aligned} γ′′=180°+∠Gc(jωc′′)G0(jωc′′)=90°+(arctan18.52ωc′′−arctanωc′′−arctan0.5ωc′′−arctan168.35ωc′′)∣ωc′′=0.54=41.44°>40°
再由 ∠ G ( j ω x ′ ′ ) = − 180 ° angle{G({rm j}omega_x'')}=-180° ∠G(jωx′′)=−180°,求得已校正系统的穿越频率: ω x ′ ′ = 1.36 r a d / s omega_x''=1.36{rm rad/s} ωx′′=1.36rad/s.故增益裕度为:
h ′ ′ ( d B ) = − 20 lg ∣ G c ( j ) ω x ′ ′ G 0 ( j ω x ′ ′ ) ∣ = 14.05 d B > 10 d B h''({rm dB})=-20lg|G_c({rm j})omega_x''G_0({rm j}omega_x'')|=14.05{rm dB}>10{rm dB} h′′(dB)=−20lg∣Gc(j)ωx′′G0(jωx′′)∣=14.05dB>10dB
满足性能要求. -
系统开环对数幅频渐近特性曲线。
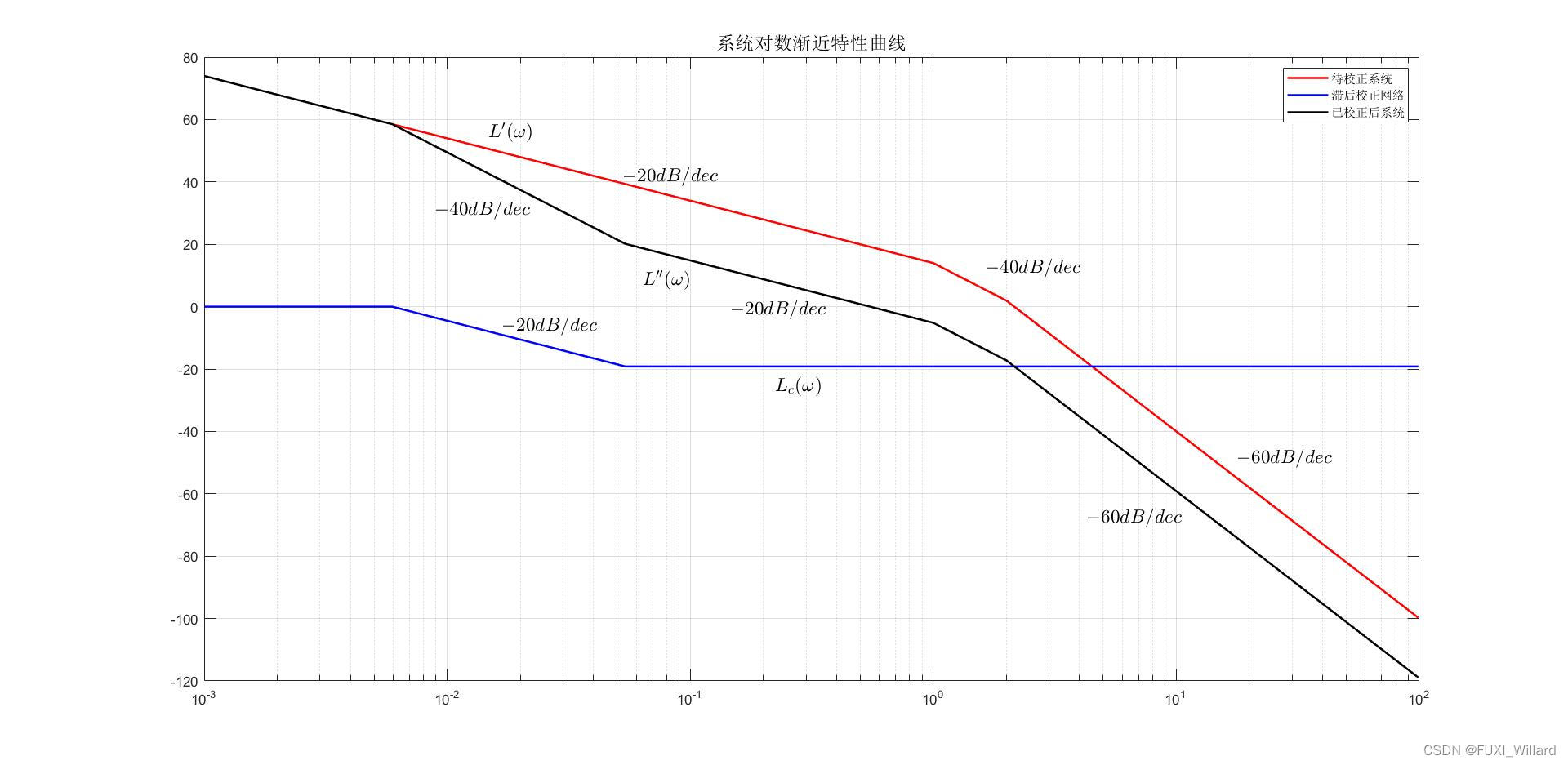
Example 6.2
设单位反馈开环传递函数为: G 0 ( s ) = K s ( s + 1 ) ( 0.2 s + 1 ) G_0(s)=displaystylefrac{K}{s(s+1)(0.2s+1)} G0(s)=s(s+1)(0.2s+1)K,设计一串联校正装置,使系统满足 K v = 8 , γ ( ω c ) = 40 ° K_v=8,gamma(omega_c)=40° Kv=8,γ(ωc)=40°,并比较校正前后的截止频率.
解:
由题意可得,取
K
=
K
v
=
8
K=K_v=8
K=Kv=8,则待校正系统的传递函数为:
G
0
(
s
)
=
8
s
(
s
+
1
)
(
0.2
s
+
1
)
G_0(s)=frac{8}{s(s+1)(0.2s+1)}
G0(s)=s(s+1)(0.2s+1)8
-
绘制待校正系统的对数幅频渐近特性曲线。
待校正系统的对数幅频渐近特性曲线如下图 L ′ ( ω ) L'(omega) L′(ω)所示.由图可得,待校正系统的截止频率为: ω c ′ = 2.83 r a d / s omega_c'=2.83{rm rad/s} ωc′=2.83rad/s,计算待校正系统的相角裕度为:
γ ′ = ( 180 ° − 90 ° − arctan ω c ′ − arctan 0.2 ω c ′ ) ∣ ω c ′ = 2.83 = − 10.05 ° gamma'=left.(180°-90°-arctanomega_c'-arctan0.2omega_c')right|_{omega_c'=2.83}=-10.05° γ′=(180°−90°−arctanωc′−arctan0.2ωc′)∣ωc′=2.83=−10.05°
表明待校正系统不稳定,故考虑采用串联滞后校正. -
由要求的 γ ′ ′ gamma'' γ′′选择 ω c ′ ′ omega_c'' ωc′′。
选取 φ ( ω c ′ ′ ) = − 6 ° varphi(omega_c'')=-6° φ(ωc′′)=−6°,要求 γ ′ ′ = 40 ° gamma''=40° γ′′=40°,则有: γ ′ ( ω c ′ ′ ) = γ ′ ′ − φ ( ω c ′ ′ ) = 46 ° gamma'(omega_c'')=gamma''-varphi(omega_c'')=46° γ′(ωc′′)=γ′′−φ(ωc′′)=46°.
由 γ ′ = 90 ° − arctan ω c ′ ′ − arctan 0.2 ω c ′ ′ gamma'=90°-arctanomega_c''-arctan0.2omega_c'' γ′=90°−arctanωc′′−arctan0.2ωc′′,解得校正后系统的截止频率: ω c ′ ′ = 0.72 r a d / s omega_c''=0.72{rm rad/s} ωc′′=0.72rad/s.
-
确定滞后网络参数 b b b和 T T T。
当 ω c ′ ′ = 0.72 r a d / s omega_c''=0.72{rm rad/s} ωc′′=0.72rad/s时,由图可测得 L ′ ( ω c ′ ′ ) = 20.92 d B L'(omega_c'')=20.92{rm dB} L′(ωc′′)=20.92dB;
再由 20 lg b = − L ′ ( ω c ′ ′ ) 20lg{b}=-L'(omega_c'') 20lgb=−L′(ωc′′),解得: b = 0.09 b=0.09 b=0.09。
令 1 b T = 0.1 ω c ′ ′ displaystylefrac{1}{bT}=0.1omega_c'' bT1=0.1ωc′′,求得: T = 154.32 T=154.32 T=154.32。
则串联滞后校正网络对数幅频渐近特性曲线如 L c ( ω ) L_c(omega) Lc(ω)所示,其传递函数为:
G c ( s ) = 1 + b T s 1 + T s = 1 + 13.89 s 1 + 154.32 s G_c(s)=frac{1+bTs}{1+Ts}=frac{1+13.89s}{1+154.32s} Gc(s)=1+Ts1+bTs=1+154.32s1+13.89s
已校正后系统的对数幅频渐近特性曲线如 L ′ ′ ( ω ) L''(omega) L′′(ω)所示,其传递函数为:
G c ( s ) G 0 ( s ) = 8 ( 13.89 s + 1 ) s ( s + 1 ) ( 0.2 s + 1 ) ( 154.32 s + 1 ) G_c(s)G_0(s)=frac{8(13.89s+1)}{s(s+1)(0.2s+1)(154.32s+1)} Gc(s)G0(s)=s(s+1)(0.2s+1)(154.32s+1)8(13.89s+1) -
验算性能指标。
γ ′ ′ = 180 ° + ∠ G c ( j ω c ′ ′ ) G 0 ( j ω c ′ ′ ) = 90 ° + ( arctan 13.89 ω c ′ ′ − arctan ω c ′ ′ − arctan 0.2 ω c ′ ′ − arctan 154.32 ω c ′ ′ ) ∣ ω c ′ ′ = 0.72 = 40.87 ° begin{aligned} gamma''&=180°+angle{G_c({rm j}omega_c'')}{G_0({rm j}omega_c'')}\\ &=left.90°+(arctan13.89omega_c''-arctanomega_c''-arctan0.2omega_c''-arctan154.32omega_c'')right|_{omega_c''=0.72}=40.87° end{aligned} γ′′=180°+∠Gc(jωc′′)G0(jωc′′)=90°+(arctan13.89ωc′′−arctanωc′′−arctan0.2ωc′′−arctan154.32ωc′′)∣ωc′′=0.72=40.87°
满足性能指标要求.系统校正前的截止频率: ω c ′ = 2.83 r a d / s omega_c'=2.83{rm rad/s} ωc′=2.83rad/s,相角裕度: γ ′ = − 10.03 ° gamma'=-10.03° γ′=−10.03°,闭环系统不稳定;采用滞后校正后的截止频率: ω c ′ ′ = 0.72 r a d / s omega_c''=0.72{rm rad/s} ωc′′=0.72rad/s,相角裕度: γ ′ ′ = 40.87 ° gamma''=40.87° γ′′=40.87°,闭环系统稳定。表明了滞后校正是通过减小系统的截止频率来提高系统的相角裕度.
-
系统开环对数幅频渐近特性曲线。
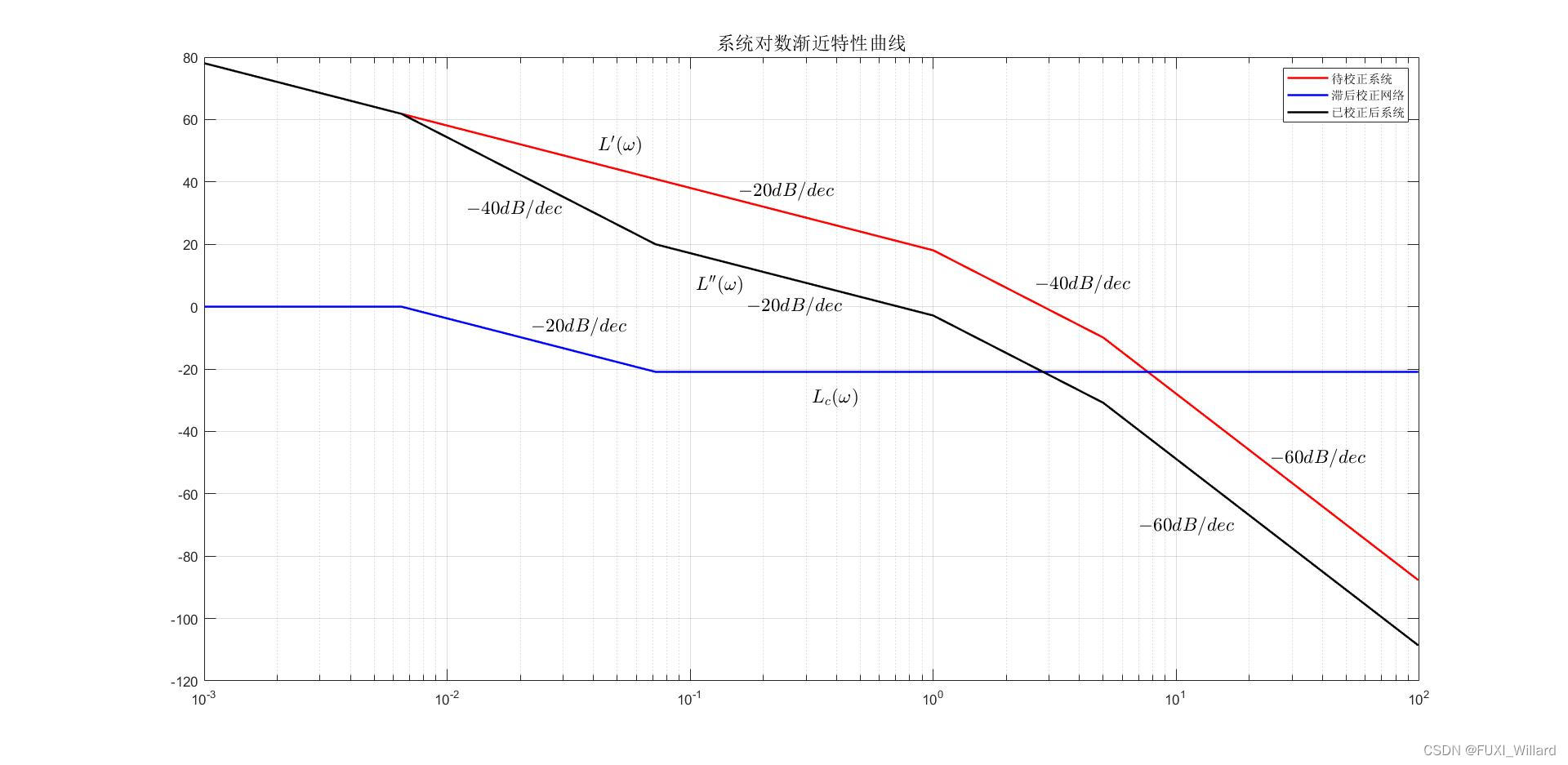
Example 6.3
设单位反馈系统的开环传递函数为: G 0 ( s ) = K s ( 0.1 s + 1 ) ( 0.2 s + 1 ) G_0(s)=displaystylefrac{K}{s(0.1s+1)(0.2s+1)} G0(s)=s(0.1s+1)(0.2s+1)K,设计校正装置,使系统的静态速度误差系数 K v = 100 K_v=100 Kv=100,相角裕度 γ ≥ 40 ° gamma≥40° γ≥40°.
解:
由题意可得,取
K
=
K
v
=
100
K=K_v=100
K=Kv=100,则待校正系统的传递函数为:
G
0
(
s
)
=
100
s
(
0.1
s
+
1
)
(
0.2
s
+
1
)
G_0(s)=frac{100}{s(0.1s+1)(0.2s+1)}
G0(s)=s(0.1s+1)(0.2s+1)100
-
绘制待校正系统的对数幅频渐近特性曲线。
待校正系统的对数幅频渐近特性曲线如下图 L ′ ( ω ) L'(omega) L′(ω)所示,待校正系统的截止频率 ω c ′ = 17.10 r a d / s omega_c'=17.10{rm rad/s} ωc′=17.10rad/s,计算待校正系统相角裕度:
γ ′ = ( 180 ° − 90 ° − arctan 0.1 ω c ′ − arctan 0.2 ω c ′ ) ∣ ω c ′ = 17.10 = − 43.38 ° gamma'=left.(180°-90°-arctan0.1omega_c'-arctan0.2omega_c')right|_{omega_c'=17.10}=-43.38° γ′=(180°−90°−arctan0.1ωc′−arctan0.2ωc′)∣ωc′=17.10=−43.38°
表明待校正系统不稳定,故考虑采用串联滞后校正. -
由要求的 γ ′ ′ gamma'' γ′′选择 ω c ′ ′ omega_c'' ωc′′。
选取 φ ( ω c ′ ′ ) = − 6 ° varphi(omega_c'')=-6° φ(ωc′′)=−6°,要求 γ ′ ′ = 40 ° gamma''=40° γ′′=40°,则有: γ ′ ( ω c ′ ′ ) = γ ′ ′ − φ ( ω c ′ ′ ) = 46 ° gamma'(omega_c'')=gamma''-varphi(omega_c'')=46° γ′(ωc′′)=γ′′−φ(ωc′′)=46°.
由 γ ′ = 90 ° − arctan 0.1 ω c ′ ′ − arctan 0.2 ω c ′ ′ gamma'=90°-arctan0.1omega_c''-arctan0.2omega_c'' γ′=90°−arctan0.1ωc′′−arctan0.2ωc′′,解得校正后系统的截止频率: ω c ′ ′ = 2.74 r a d / s omega_c''=2.74{rm rad/s} ωc′′=2.74rad/s.
-
确定滞后网络参数 b b b和 T T T。
当 ω c ′ ′ = 2.74 r a d / s omega_c''=2.74{rm rad/s} ωc′′=2.74rad/s时,由图可测得 L ′ ( ω c ′ ′ ) = 31.24 d B L'(omega_c'')=31.24{rm dB} L′(ωc′′)=31.24dB;
由 20 lg b = − L ′ ( ω c ′ ′ ) 20lg{b}=-L'(omega_c'') 20lgb=−L′(ωc′′),解得: b = 0.0274 b=0.0274 b=0.0274,取 b = 0.03 b=0.03 b=0.03。
令 1 b T = 0.1 ω c ′ ′ displaystylefrac{1}{bT}=0.1omega_c'' bT1=0.1ωc′′,解得: T = 121.65 T=121.65 T=121.65。
则串联滞后校正网络的对数幅频渐近特性如 L c ( ω ) L_c(omega) Lc(ω)所示,其传递函数为:
G c ( s ) = 1 + b T s 1 + T s = 1 + 3.65 s 1 + 121.65 s G_c(s)=frac{1+bTs}{1+Ts}=frac{1+3.65s}{1+121.65s} Gc(s)=1+Ts1+bTs=1+121.65s1+3.65s
已校正系统的开环对数幅频渐近特性曲线如下图 L ′ ′ ( ω ) L''(omega) L′′(ω)所示,其传递函数为:
G c ( s ) G 0 ( s ) = 100 ( 3.65 s + 1 ) s ( 0.1 s + 1 ) ( 0.2 s + 1 ) ( 121.65 s + 1 ) G_c(s)G_0(s)=frac{100(3.65s+1)}{s(0.1s+1)(0.2s+1)(121.65s+1)} Gc(s)G0(s)=s(0.1s+1)(0.2s+1)(121.65s+1)100(3.65s+1) -
验算性能指标。
γ ′ ′ = 180 ° + ∠ G c ( j ω c ′ ′ ) G 0 ( j ω c ′ ′ ) = 90 ° + ( arctan 3.65 ω c ′ ′ − arctan 0.1 ω c ′ ′ − arctan 0.2 ω c ′ ′ − arctan 121.65 ω c ′ ′ ) ∣ ω c ′ ′ = 2.74 = 40.42 ° begin{aligned} gamma''&=180°+angle{G_c({rm j}omega_c'')G_0({rm j}omega_c'')}\\ &=left.90°+(arctan3.65omega_c''-arctan0.1omega_c''-arctan0.2omega_c''-arctan121.65omega_c'')right|_{omega_c''=2.74}=40.42° end{aligned} γ′′=180°+∠Gc(jωc′′)G0(jωc′′)=90°+(arctan3.65ωc′′−arctan0.1ωc′′−arctan0.2ωc′′−arctan121.65ωc′′)∣ωc′′=2.74=40.42°
满足性能指标要求。 -
系统开环对数幅频渐近特性曲线。
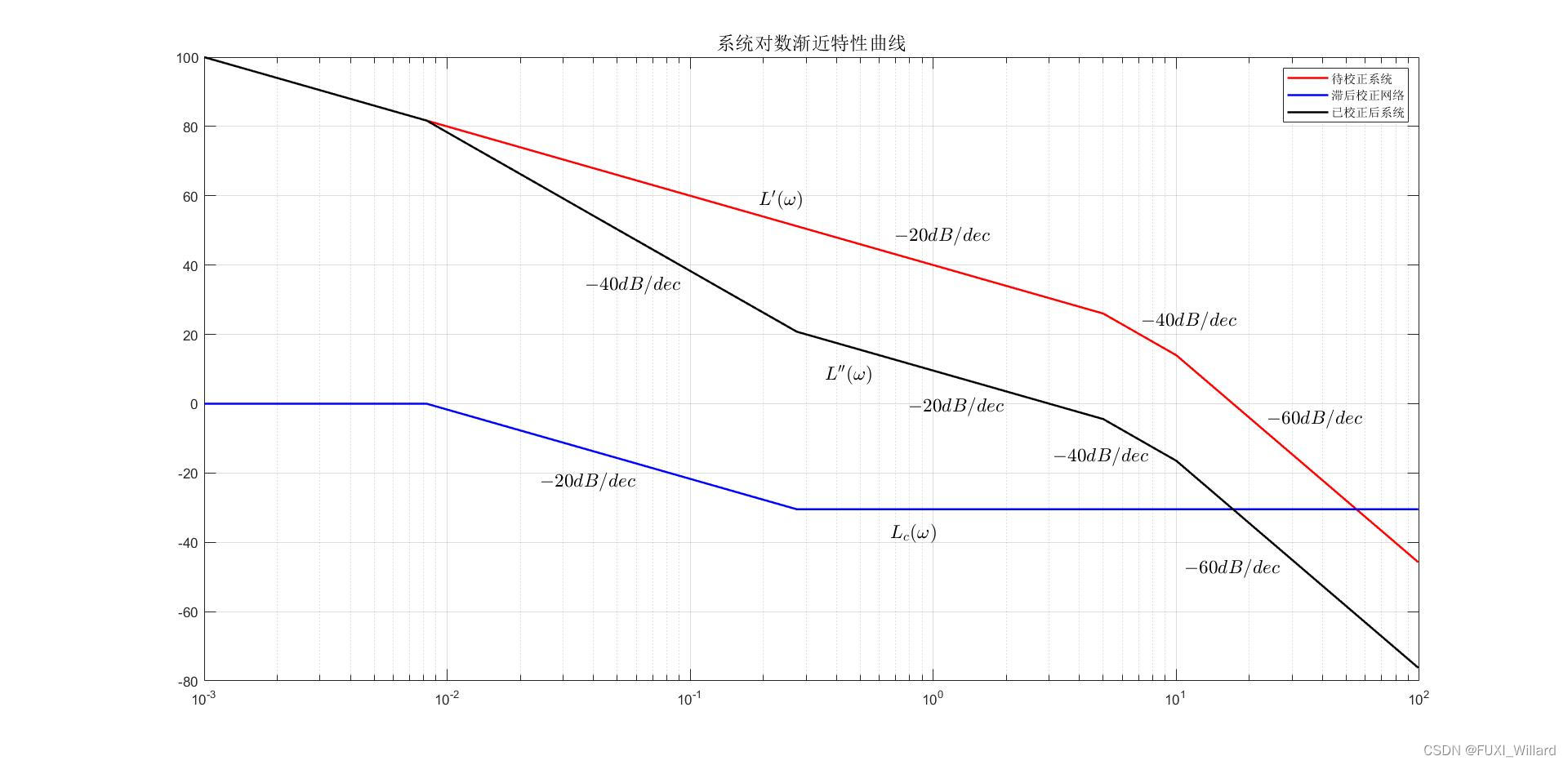
Example 6.4
设单位反馈系统的开环传递函数为: G 0 ( s ) = K s ( s + 1 ) G_0(s)=displaystylefrac{K}{s(s+1)} G0(s)=s(s+1)K,设计串联校正装置,使校正后系统的阻尼比: ζ = 0.7 zeta=0.7 ζ=0.7,调节时间为: t s = 1.4 ( Δ = 5 % ) t_s=1.4(Delta=5%) ts=1.4(Δ=5%),速度误差系数: K v ≥ 2 K_v≥2 Kv≥2.
解:
令串联校正装置传递函数为:
G
c
(
s
)
=
p
(
s
+
1
)
s
+
p
G_c(s)=frac{p(s+1)}{s+p}
Gc(s)=s+pp(s+1)
校正后系统开环传递函数:
G
(
s
)
=
G
0
(
s
)
G
c
(
s
)
=
p
K
s
(
s
+
p
)
G(s)=G_0(s)G_c(s)=frac{pK}{s(s+p)}
G(s)=G0(s)Gc(s)=s(s+p)pK
校正后系统闭环传递函数:
Φ
(
s
)
=
K
p
s
2
+
p
s
+
K
p
Phi(s)=frac{Kp}{s^2+ps+Kp}
Φ(s)=s2+ps+KpKp
则
ω
n
=
K
p
,
2
ζ
ω
n
=
p
omega_n=sqrt{Kp},2zetaomega_n=p
ωn=Kp,2ζωn=p
由校正后系统的调节时间:
t
s
=
1.4
t_s=1.4
ts=1.4,即:
3.5
ζ
ω
n
=
1.4
displaystylefrac{3.5}{zetaomega_n}=1.4
ζωn3.5=1.4;由校正后系统阻尼比为:
ζ
=
0.7
zeta=0.7
ζ=0.7,解得:
ω
n
=
3.57
omega_n=3.57
ωn=3.57。
由 ω n = K p omega_n=sqrt{Kp} ωn=Kp和 2 ζ ω n = p 2zetaomega_n=p 2ζωn=p,解得: p = 5.0 , K = 2.55 p=5.0,K=2.55 p=5.0,K=2.55。
由已校正系统的开环传递函数,可知: K v = K = 2.55 > 2 K_v=K=2.55>2 Kv=K=2.55>2,满足设计要求.
所以,串联校正装置传递函数为:
G
c
(
s
)
=
5
(
s
+
1
)
s
+
5
G_c(s)=frac{5(s+1)}{s+5}
Gc(s)=s+55(s+1)
Example 6.5
设单位反馈系统的开环传递函数为: G 0 ( s ) = K s ( 0.05 s + 1 ) ( 0.2 s + 1 ) G_0(s)=displaystylefrac{K}{s(0.05s+1)(0.2s+1)} G0(s)=s(0.05s+1)(0.2s+1)K,设计串联校正装置,使系统的静态误差系数不小于 5 5 5,超调量不大于 25 % 25% 25%,调节时间不大于 1 s 1{rm s} 1s.
解:
由题意,取
K
=
K
v
=
5
K=K_v=5
K=Kv=5,则待校正系统的传递函数为:
G
0
(
s
)
=
5
s
(
0.05
s
+
1
)
(
0.2
s
+
1
)
G_0(s)=frac{5}{s(0.05s+1)(0.2s+1)}
G0(s)=s(0.05s+1)(0.2s+1)5
-
绘制待校正系统的对数幅频渐近特性曲线。
待校正系统对数幅频渐近特性曲线如下图 L ′ ( ω ) L'(omega) L′(ω)所示,由图可得,待校正系统的截止频率: ω c ′ = 5 r a d / s omega_c'=5{rm rad/s} ωc′=5rad/s,计算待校正系统的相角裕度为:
γ ′ = ( 180 ° − 90 ° − arctan 0.05 ω c ′ − arctan 0.2 ω c ′ ) ∣ ω c ′ = 5 = 30.96 ° gamma'=left.(180°-90°-arctan0.05omega_c'-arctan0.2omega_c')right|_{omega_c'=5}=30.96° γ′=(180°−90°−arctan0.05ωc′−arctan0.2ωc′)∣ωc′=5=30.96° -
将 σ % 、 t s sigma%、t_s σ%、ts转换为相应的频域指标。
由
σ % = [ 0.16 + 0.4 ( M r − 1 ) ] × 100 % ≤ 25 % t s = K 0 π ω c ≤ 1 , K 0 = 2 + 1.5 ( M r − 1 ) + 2.5 ( M r − 1 ) 2 begin{aligned} &sigma%=[0.16+0.4(M_r-1)]times100%≤25%\\ &t_s=frac{K_0pi}{omega_c}≤1,K_0=2+1.5(M_r-1)+2.5(M_r-1)^2 end{aligned} σ%=[0.16+0.4(Mr−1)]×100%≤25%ts=ωcK0π≤1,K0=2+1.5(Mr−1)+2.5(Mr−1)2
求得:
M r ≤ 1.225 , ω c ≥ 7.74 r a d / s M_r≤1.225,omega_c≥7.74{rm rad/s} Mr≤1.225,ωc≥7.74rad/s
由 M r = 1 sin γ M_r=displaystylefrac{1}{singamma} Mr=sinγ1,解得: γ ≥ 54.72 ° gamma≥54.72° γ≥54.72°。由于 ω c > ω c ′ omega_c>omega_c' ωc>ωc′,故考虑采用超前校正.
-
确定超前网络参数 a a a和 T T T。
选取 ω c ′ ′ = 8 r a d / s omega_c''=8{rm rad/s} ωc′′=8rad/s时,由图可测得: L ′ ( ω c ′ ′ ) = − 8.16 d B L'(omega_c'')=-8.16{rm dB} L′(ωc′′)=−8.16dB;
由 10 lg a = − L ′ ( ω c ′ ′ ) 10lg{a}=-L'(omega_c'') 10lga=−L′(ωc′′),解得: a = 6.55 a=6.55 a=6.55。令 T = 1 ω c ′ ′ a T=displaystylefrac{1}{omega_c''sqrt{a}} T=ωc′′a1,求得: T = 0.049 T=0.049 T=0.049。
串联超前校正网络的对数幅频渐近特性曲线如 L c ( ω ) L_c(omega) Lc(ω)所示,其传递函数为:
a G c ( s ) = 1 + a T s 1 + T s = 1 + 0.32 s 1 + 0.049 s aG_c(s)=frac{1+aTs}{1+Ts}=frac{1+0.32s}{1+0.049s} aGc(s)=1+Ts1+aTs=1+0.049s1+0.32s
将放大器增益提高 a a a倍,校正后系统的对数幅频渐近特性曲线如 L ′ ′ ( ω ) L''(omega) L′′(ω)所示,其传递函数为:
a G c ( s ) G 0 ( s ) = 5 ( 0.32 s + 1 ) s ( 0.05 s + 1 ) ( 0.2 s + 1 ) ( 0.049 s + 1 ) aG_c(s)G_0(s)=frac{5(0.32s+1)}{s(0.05s+1)(0.2s+1)(0.049s+1)} aGc(s)G0(s)=s(0.05s+1)(0.2s+1)(0.049s+1)5(0.32s+1) -
性能指标验算。
γ ′ ′ = 180 ° + ∠ a G c ( j ω c ′ ′ ) G 0 ( j ω c ′ ′ ) = 90 ° + ( arctan 0.32 ω c ′ ′ − arctan 0.05 ω c ′ ′ − arctan 0.2 ω c ′ ′ − arctan 0.049 ω c ′ ′ ) ∣ ω c ′ ′ = 8 = 57.46 ° > 54.72 ° begin{aligned} gamma''&=180°+angle{aG_c({rm j}omega_c'')G_0({rm j}omega_c'')}\\ &=left.90°+(arctan0.32omega_c''-arctan0.05omega_c''-arctan0.2omega_c''-arctan0.049omega_c'')right|_{omega_c''=8}\\ &=57.46°>54.72° end{aligned} γ′′=180°+∠aGc(jωc′′)G0(jωc′′)=90°+(arctan0.32ωc′′−arctan0.05ωc′′−arctan0.2ωc′′−arctan0.049ωc′′)∣ωc′′=8=57.46°>54.72° -
系统开环对数幅频渐近特性曲线。
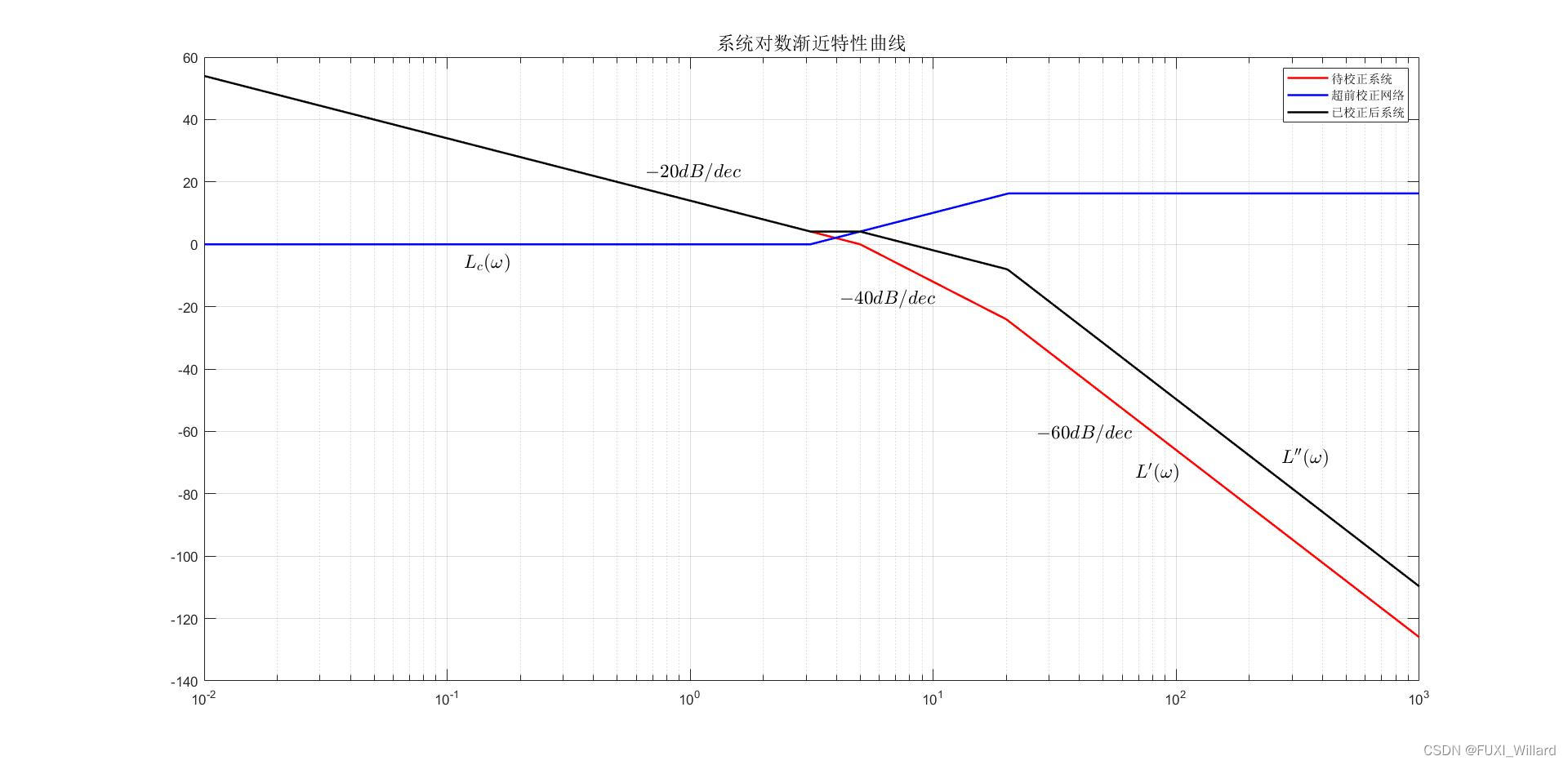
Example 6.6
设单位反馈系统的开环传递函数为: G 0 ( s ) = K s ( 0.05 s + 1 ) ( 0.25 s + 1 ) ( 0.1 s + 1 ) G_0(s)=displaystylefrac{K}{s(0.05s+1)(0.25s+1)(0.1s+1)} G0(s)=s(0.05s+1)(0.25s+1)(0.1s+1)K,若要求校正后系统的开环增益不小于 12 12 12,超调量小于 30 % 30% 30%,调节时间小于 6 s ( Δ = 5 % ) 6s(Delta=5%) 6s(Δ=5%),确定串联滞后校正装置的传递函数。
解:
由题意,取
K
=
12
K=12
K=12,则待校正系统的传递函数为:
G
0
(
s
)
=
12
s
(
0.05
s
+
1
)
(
0.25
s
+
1
)
(
0.1
s
+
1
)
G_0(s)=frac{12}{s(0.05s+1)(0.25s+1)(0.1s+1)}
G0(s)=s(0.05s+1)(0.25s+1)(0.1s+1)12
-
绘制待校正系统的对数幅频渐近特性曲线。
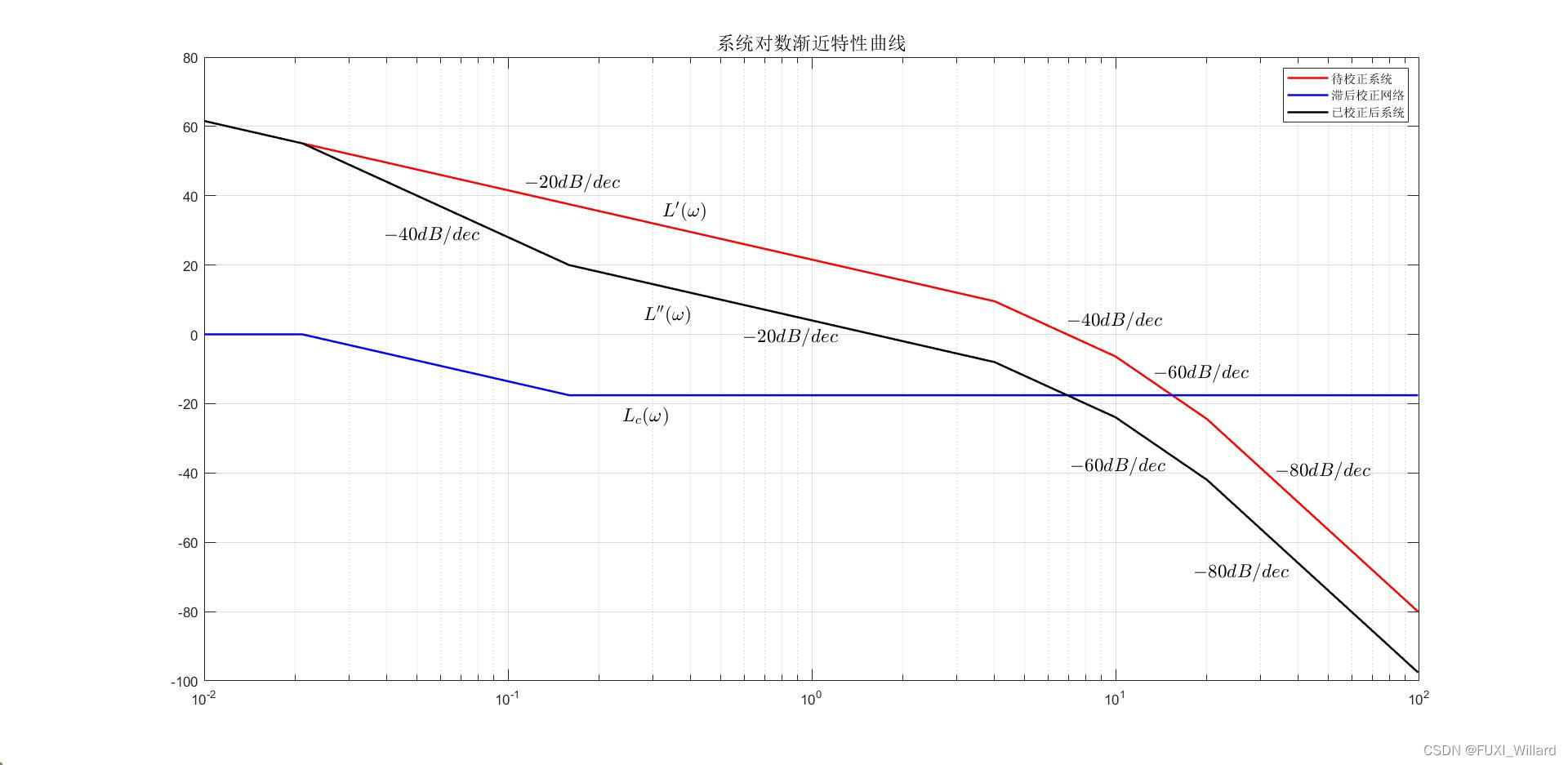
待校正系统对数幅频渐近特性曲线如下图 L ′ ( ω ) L'(omega) L′(ω)所示,由图可得,待校正系统的截止频率: ω c ′ = 6.93 r a d / s omega_c'=6.93{rm rad/s} ωc′=6.93rad/s,计算待校正系统的相角裕度为:
γ ′ = ( 180 ° − 90 ° − arctan 0.05 ω c ′ − arctan 0.25 ω c ′ − arctan 0.1 ω c ′ ) ∣ ω c ′ = 6.93 = − 23.83 ° gamma'=left.(180°-90°-arctan0.05omega_c'-arctan0.25omega_c'-arctan0.1omega_c')right|_{omega_c'=6.93}=-23.83° γ′=(180°−90°−arctan0.05ωc′−arctan0.25ωc′−arctan0.1ωc′)∣ωc′=6.93=−23.83°
表明待校正系统不稳定. -
将 σ % 、 t s sigma%、t_s σ%、ts转换为相应的频域指标。
由
σ % = [ 0.16 + 0.4 ( M r − 1 ) ] × 100 % < 30 % t s = K 0 π ω c < 6 , K 0 = 2 + 1.5 ( M r − 1 ) + 2.5 ( M r − 1 ) 2 begin{aligned} &sigma%=[0.16+0.4(M_r-1)]times100%<30%\\ &t_s=frac{K_0pi}{omega_c}<6,K_0=2+1.5(M_r-1)+2.5(M_r-1)^2 end{aligned} σ%=[0.16+0.4(Mr−1)]×100%<30%ts=ωcK0π<6,K0=2+1.5(Mr−1)+2.5(Mr−1)2
解得:
M r < 1.35 , ω c > 1.48 r a d / s M_r<1.35,omega_c>1.48{rm rad/s} Mr<1.35,ωc>1.48rad/s
由 M r = 1 sin γ M_r=displaystylefrac{1}{singamma} Mr=sinγ1,解得: γ > 47.79 ° gamma>47.79° γ>47.79°。由于 γ ′ < 0 gamma'<0 γ′<0和 ω c < ω c ′ omega_c<omega_c' ωc<ωc′,故考虑采用滞后校正。
-
由要求的 γ ′ ′ gamma'' γ′′选择 ω c ′ ′ omega_c'' ωc′′。
选取 φ ( ω c ′ ′ ) = − 6 ° varphi(omega_c'')=-6° φ(ωc′′)=−6°,要求 γ > 47.79 ° gamma>47.79° γ>47.79°,选取 γ ′ ′ = 48 ° gamma''=48° γ′′=48°.有 γ ′ ( ω c ′ ′ ) = γ ′ ′ − φ ( ω c ′ ′ ) = 54 ° gamma'(omega_c'')=gamma''-varphi(omega_c'')=54° γ′(ωc′′)=γ′′−φ(ωc′′)=54°.
由
γ ′ ′ = 90 ° − arctan 0.05 ω c ′ ′ − arctan 0.25 ω c ′ ′ − arctan 0.1 ω c ′ ′ ⇒ ω c ′ ′ = 1.59 r a d / s gamma''=90°-arctan0.05omega_c''-arctan0.25omega_c''-arctan0.1omega_c''Rightarrowomega_c''=1.59{rm rad/s} γ′′=90°−arctan0.05ωc′′−arctan0.25ωc′′−arctan0.1ωc′′⇒ωc′′=1.59rad/s -
确定滞后网络参数 b b b和 T T T。
当 ω c ′ ′ = 1.59 r a d / s omega_c''=1.59{rm rad/s} ωc′′=1.59rad/s时,由图可测得: L ′ ( ω c ′ ′ ) = 17.56 d B L'(omega_c'')=17.56{rm dB} L′(ωc′′)=17.56dB.由 20 lg b = − L ′ ( ω c ′ ′ ) 20lg{b}=-L'(omega_c'') 20lgb=−L′(ωc′′),解得: b = 0.1325 b=0.1325 b=0.1325。
令 1 b T = 0.1 ω c ′ ′ displaystylefrac{1}{bT}=0.1omega_c'' bT1=0.1ωc′′,解得: T = 47.47 T=47.47 T=47.47。
则串联滞后校正网络对数幅频渐近特性曲线如 L c ( ω ) L_c(omega) Lc(ω)所示,其传递函数为:
G c ( s ) = 1 + b T s 1 + T s = 1 + 6.29 s 1 + 47.47 s G_c(s)=frac{1+bTs}{1+Ts}=frac{1+6.29s}{1+47.47s} Gc(s)=1+Ts1+bTs=1+47.47s1+6.29s
校正后系统开环对数幅频渐近特性曲线如 L ′ ′ ( ω ) L''(omega) L′′(ω)所示,其传递函数为:
G c ( s ) G 0 ( s ) = 12 ( 6.29 s + 1 ) s ( 0.05 s + 1 ) ( 0.25 s + 1 ) ( 0.1 s + 1 ) ( 47.47 s + 1 ) G_c(s)G_0(s)=frac{12(6.29s+1)}{s(0.05s+1)(0.25s+1)(0.1s+1)(47.47s+1)} Gc(s)G0(s)=s(0.05s+1)(0.25s+1)(0.1s+1)(47.47s+1)12(6.29s+1) -
验算性能指标。
γ ′ ′ = 180 ° + ∠ G c ( j ω c ′ ′ ) G 0 ( j ω c ′ ′ ) = ( 90 ° + arctan 6.29 ω c ′ ′ − arctan 0.05 ω c ′ ′ − arctan 0.25 ω c ′ ′ − arctan 0.1 ω c ′ ′ − arctan 47.47 ω c ′ ′ ) ∣ ω c ′ ′ = 1.59 = 49.79 ° > 47.79 ° begin{aligned} gamma''&=180°+angle{G_c({rm j}omega_c'')G_0({rm j}omega_c'')}\\ &=(90°+arctan6.29omega_c''-arctan0.05omega_c''-arctan0.25omega_c'' -arctan0.1omega_c''\\ &-left.arctan47.47omega_c'')right|_{omega_c''=1.59}=49.79°>47.79° end{aligned} γ′′=180°+∠Gc(jωc′′)G0(jωc′′)=(90°+arctan6.29ωc′′−arctan0.05ωc′′−arctan0.25ωc′′−arctan0.1ωc′′−arctan47.47ωc′′)∣ωc′′=1.59=49.79°>47.79°
所以,各项性能指标均满足要求. -
系统开环对数幅频渐近特性曲线。
Example 6.7
已知待校正系统开环传递函数为: G 0 ( s ) = 10 s ( 0.25 s + 1 ) ( 0.05 s + 1 ) G_0(s)=displaystylefrac{10}{s(0.25s+1)(0.05s+1)} G0(s)=s(0.25s+1)(0.05s+1)10,若要求校正后系统的谐振峰值: M r = 1.4 M_r=1.4 Mr=1.4,谐振频率: ω r > 8 omega_r>8 ωr>8,确定校正装置.
解:
由校正后系统的谐振峰值要求: M r = 1.4 M_r=1.4 Mr=1.4和 M r = 1 sin γ M_r=displaystylefrac{1}{singamma} Mr=sinγ1,解得已校正系统的相角裕度为: γ = 45.58 ° gamma=45.58° γ=45.58°。
-
绘制待校正系统的对数幅频渐近特性曲线。
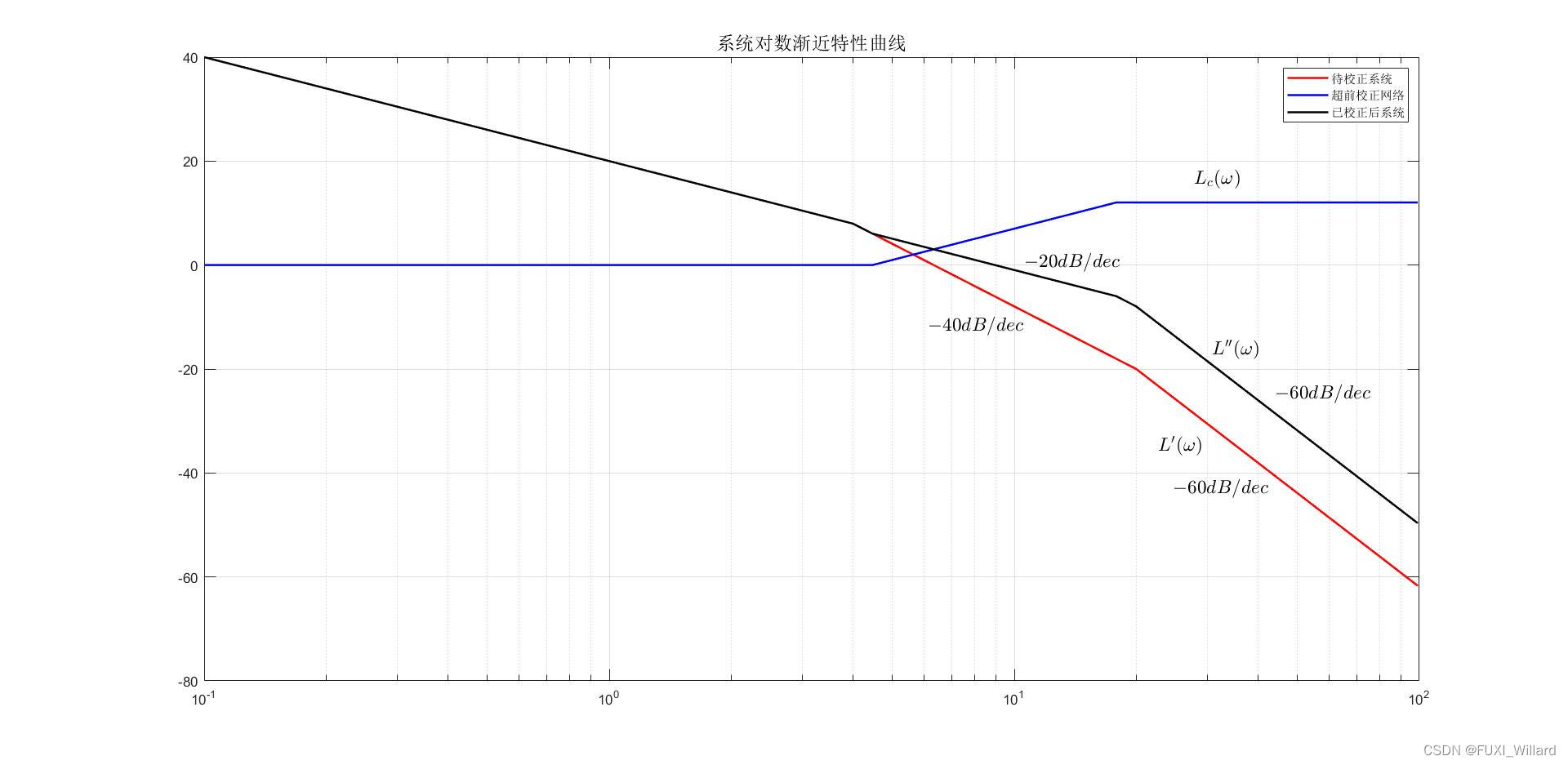
待校正系统的对数幅频渐近特性曲线如 L ′ ( ω ) L'(omega) L′(ω)所示,由图可得,待校正系统的截止频率为: ω c ′ = 6.32 r a d / s omega_c'=6.32{rm rad/s} ωc′=6.32rad/s.计算待校正系统的相角裕度为:
γ ′ = ( 180 ° − 90 ° − arctan 0.25 ω c ′ − arctan 0.05 ω c ′ ) ∣ ω c ′ = 6.32 = 14.79 ° < γ gamma'=left.(180°-90°-arctan0.25omega_c'-arctan0.05omega_c')right|_{omega_c'=6.32}=14.79°<gamma γ′=(180°−90°−arctan0.25ωc′−arctan0.05ωc′)∣ωc′=6.32=14.79°<γ
故考虑采用超前校正. -
确定超前网络参数 a a a和 T T T.
取 ω c ′ ′ = 9 r a d / s omega_c''=9{rm rad/s} ωc′′=9rad/s时,由图可测得: L ′ ( ω c ′ ′ ) = − 6.13 d B L'(omega_c'')=-6.13{rm dB} L′(ωc′′)=−6.13dB;由 10 lg a = − L ′ ( ω c ′ ′ ) 10lg{a}=-L'(omega_c'') 10lga=−L′(ωc′′),解得: a = 4.1 a=4.1 a=4.1。
令 T = 1 ω c ′ ′ a T=displaystylefrac{1}{omega_c''sqrt{a}} T=ωc′′a1,求得: T = 0.056 T=0.056 T=0.056。
则串联超前校正网络的对数幅频渐近特性曲线如 L c ( ω ) L_c(omega) Lc(ω)所示,其传递函数为:
a G c ( s ) = 1 + a T s 1 + T s = 1 + 0.224 s 1 + 0.056 s aG_c(s)=frac{1+aTs}{1+Ts}=frac{1+0.224s}{1+0.056s} aGc(s)=1+Ts1+aTs=1+0.056s1+0.224s
将放大器增益提高 a a a倍,已校正系统的开环对数幅频渐近特性曲线如 L ′ ′ ( ω ) L''(omega) L′′(ω)所示,其传递函数为:
G ( s ) = 10 ( 0.224 s + 1 ) s ( 0.05 s + 1 ) ( 0.25 s + 1 ) ( 0.056 s + 1 ) G(s)=frac{10(0.224s+1)}{s(0.05s+1)(0.25s+1)(0.056s+1)} G(s)=s(0.05s+1)(0.25s+1)(0.056s+1)10(0.224s+1) -
系统开环对数幅频渐近特性曲线。
Example 6.8
已知系统开环传递函数为: G ( s ) = K s ( 1 + 0.5 s ) ( 1 + 0.1 s ) G(s)=displaystylefrac{K}{s(1+0.5s)(1+0.1s)} G(s)=s(1+0.5s)(1+0.1s)K,设计 P I D {rm PID} PID校正装置,使系统 K v ≥ 10 , γ ( ω c ′ ′ ) ≥ 50 ° K_v≥10,gamma(omega_c'')≥50° Kv≥10,γ(ωc′′)≥50°,且 ω c ′ ′ ≥ 4 omega_c''≥4 ωc′′≥4.
解:
令
K
=
K
v
=
10
K=K_v=10
K=Kv=10,作校正系统如下图
L
′
(
ω
)
L'(omega)
L′(ω)所示:
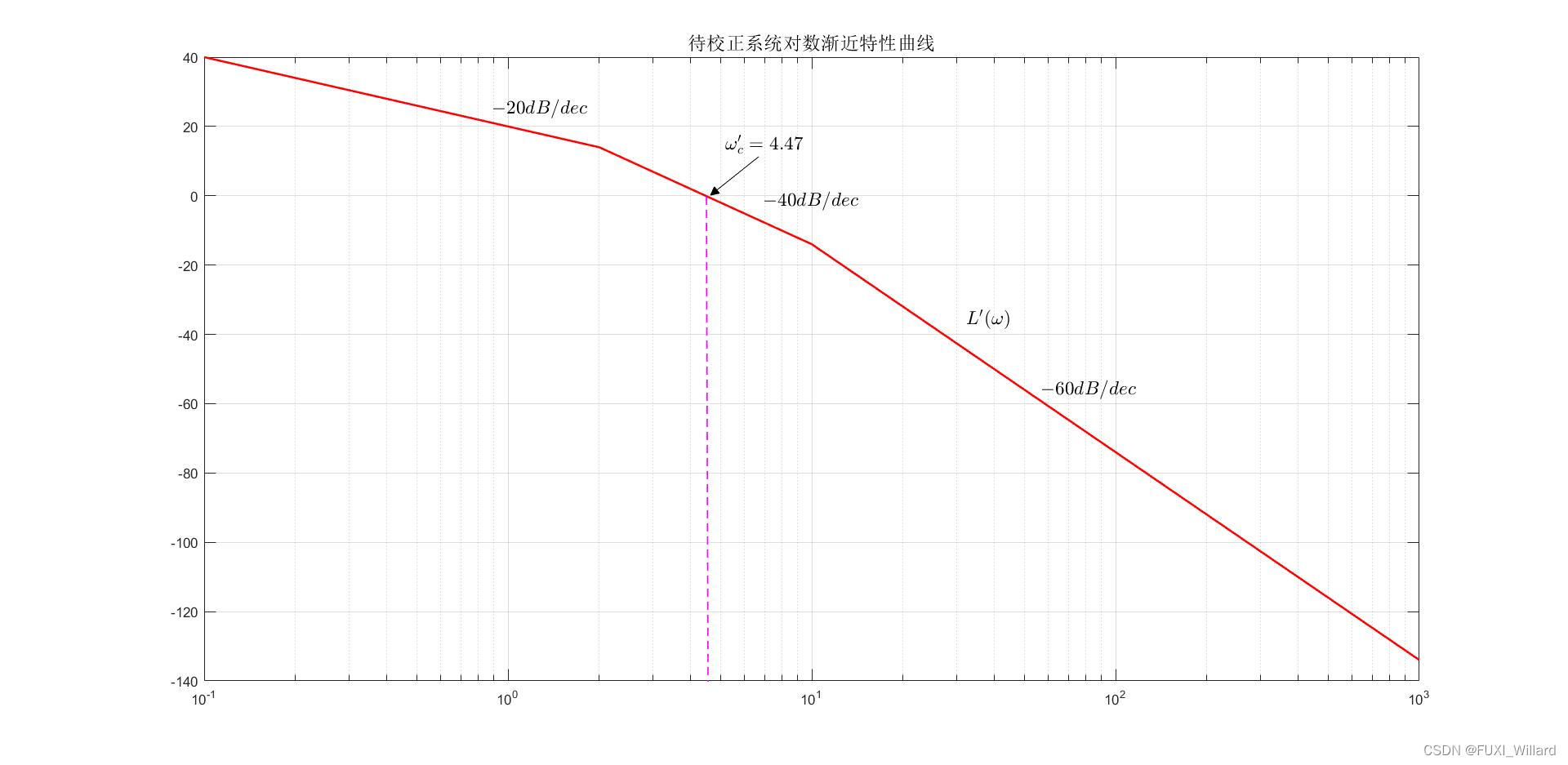
由图可知,
ω
c
′
=
4.47
,
γ
(
ω
c
′
)
≈
0
°
omega_c'=4.47,gamma(omega_c')≈0°
ωc′=4.47,γ(ωc′)≈0°。
设
P
I
D
{rm PID}
PID校正装置传递函数为:
G
c
(
s
)
=
(
1
+
τ
1
s
)
(
1
+
τ
2
s
)
τ
1
s
+
1
=
(
1
+
s
/
ω
1
)
(
1
+
s
/
ω
2
)
s
/
ω
1
G_c(s)=frac{(1+tau_1s)(1+tau_2s)}{tau_1s+1}=frac{(1+s/omega_1)(1+s/omega_2)}{s/omega_1}
Gc(s)=τ1s+1(1+τ1s)(1+τ2s)=s/ω1(1+s/ω1)(1+s/ω2)
则校正后系统频率特性为:
G
(
j
ω
)
G
c
(
j
ω
)
=
K
1
(
1
+
j
ω
/
ω
1
)
(
1
+
j
ω
/
ω
2
)
(
j
ω
)
2
(
1
+
j
ω
/
2
)
(
1
+
j
ω
/
10
)
,
K
1
=
K
ω
1
G({rm j}omega)G_c({rm j}omega)=frac{K_1(1+{rm j}omega/omega_1)(1+{rm j}omega/omega_2)}{({rm j}omega)^2(1+{rm j}omega/2)(1+{rm j}omega/10)},K_1=Komega_1
G(jω)Gc(jω)=(jω)2(1+jω/2)(1+jω/10)K1(1+jω/ω1)(1+jω/ω2),K1=Kω1
由于校正后为Ⅱ型系统,故
K
v
K_v
Kv的要求肯定满足,系统开环增益可任选,由其他条件而定.
初选
ω
c
′
′
=
4
omega_c''=4
ωc′′=4。为降低系统阶次,选
ω
2
=
2
omega_2=2
ω2=2,并选
ω
1
=
0.4
omega_1=0.4
ω1=0.4,可得:
G
(
j
ω
)
G
c
(
j
ω
)
=
K
1
(
1
+
j
ω
/
0.4
)
(
j
ω
)
2
(
1
+
j
ω
/
10
)
G({rm j}omega)G_c({rm j}omega)=frac{K_1(1+{rm j}omega/0.4)}{({rm j}omega)^2(1+{rm j}omega/10)}
G(jω)Gc(jω)=(jω)2(1+jω/10)K1(1+jω/0.4)
其对应幅频特性应通过截止频率
ω
c
′
′
=
4
omega_c''=4
ωc′′=4,故由近似式:
K
1
ω
c
′
′
/
0.4
(
ω
c
′
′
)
2
=
1
⇒
K
1
=
1.6
,
K
=
4
frac{K_1omega_c''/0.4}{(omega_c'')^2}=1Rightarrow{K_1=1.6},K=4
(ωc′′)2K1ωc′′/0.4=1⇒K1=1.6,K=4
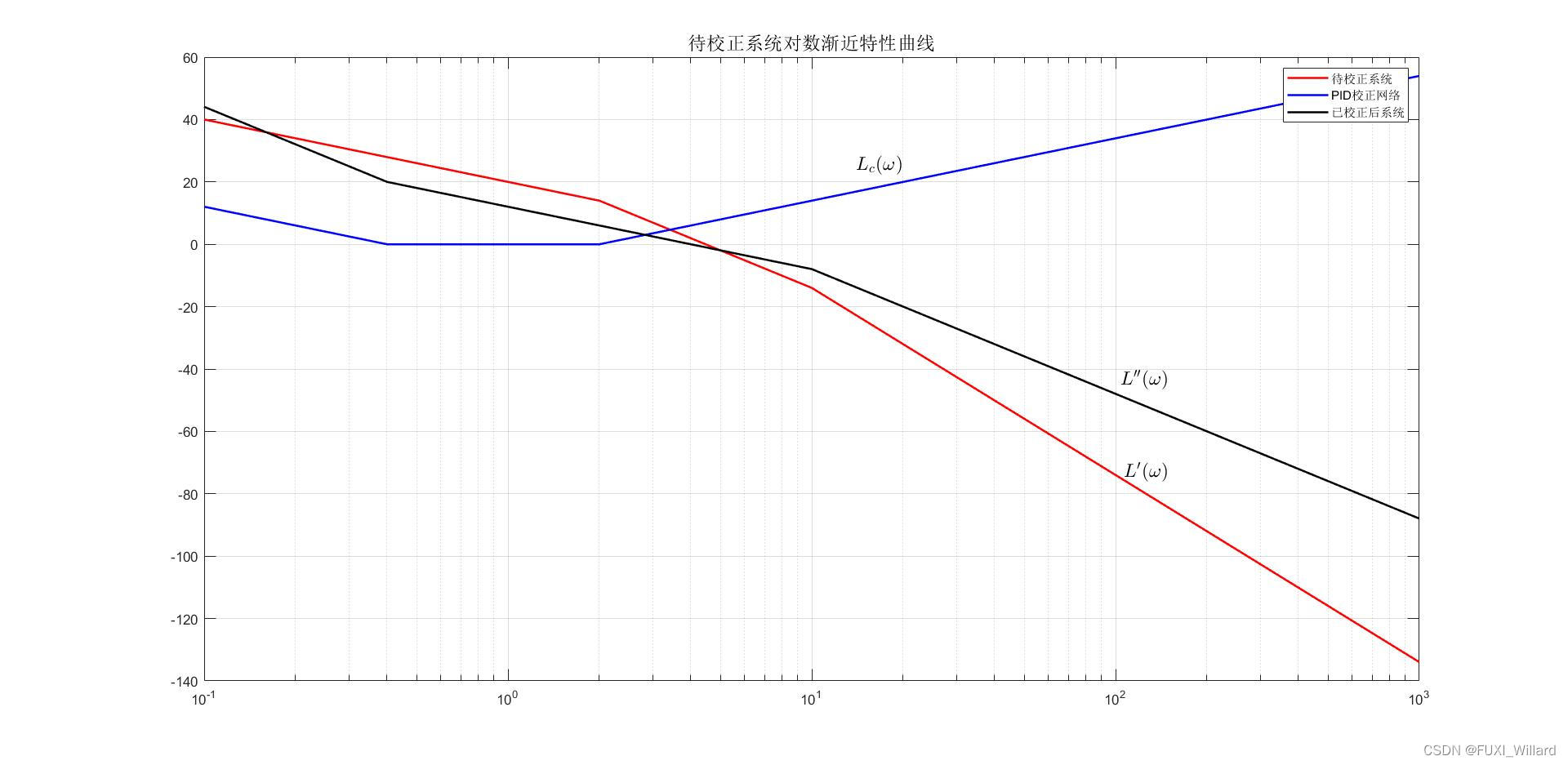
已校正系统开环幅频渐近特性曲线如下图
L
′
′
(
ω
)
L''(omega)
L′′(ω)所示:
验算:
γ
(
ω
c
′
′
)
=
arctan
ω
c
′
′
0.4
−
arctan
ω
c
′
′
10
=
62.5
°
gamma(omega_c'')=frac{arctanomega_c''}{0.4}-frac{arctanomega_c''}{10}=62.5°
γ(ωc′′)=0.4arctanωc′′−10arctanωc′′=62.5°
全部满足设计指标要求.
Example 6.9
设具有反馈校正的系统结构图如下图所示,待校正对象的开环传递函数为: G 0 ( s ) = G 1 ( s ) G 2 ( s ) G_0(s)=G_1(s)G_2(s) G0(s)=G1(s)G2(s),其中: G 1 ( s ) = K 1 s ( T 1 s + 1 ) , K 1 = 100 , T 1 = 1.1 ; G 2 ( s ) = 1 T 2 s + 1 , T 2 = 0.025 G_1(s)=displaystylefrac{K_1}{s(T_1s+1)},K_1=100,T_1=1.1;G_2(s)=displaystylefrac{1}{T_2s+1},T_2=0.025 G1(s)=s(T1s+1)K1,K1=100,T1=1.1;G2(s)=T2s+11,T2=0.025。局部反馈校正装置的传递函数为 H ( s ) = 0.25 s H(s)=0.25s H(s)=0.25s。绘制校正前后系统的对数幅频渐近特性,写出等效开环传递函数 G k ( s ) G_k(s) Gk(s),并计算已校正系统的相角裕度 γ ( ω c ) gamma(omega_c) γ(ωc)。
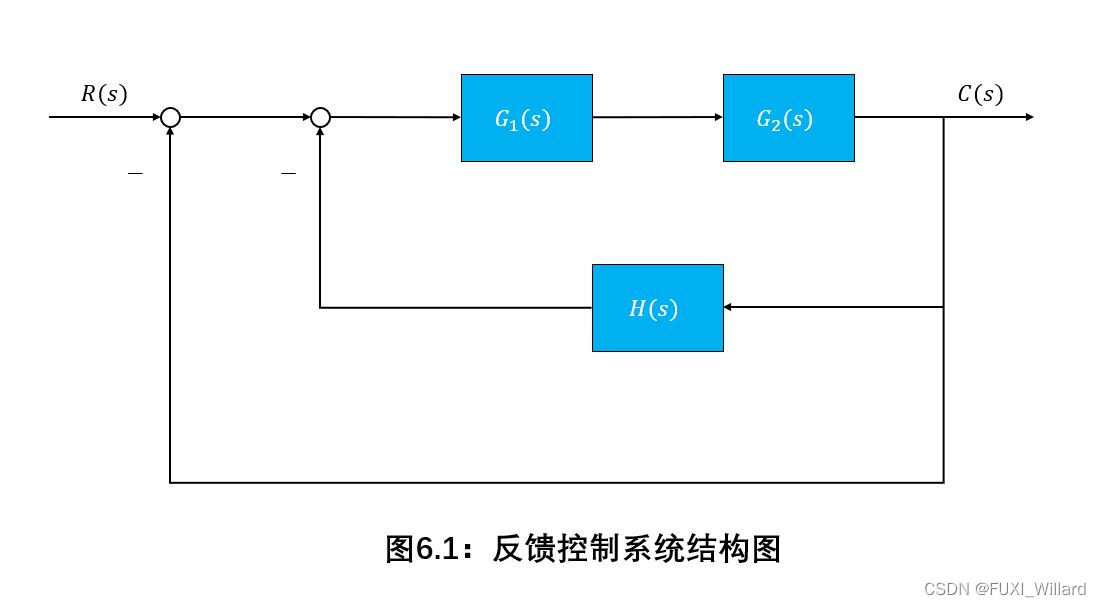
解:
待校正系统的传递函数为:
G
0
(
s
)
=
100
s
(
0.025
s
+
1
)
(
1.1
s
+
1
)
G_0(s)=frac{100}{s(0.025s+1)(1.1s+1)}
G0(s)=s(0.025s+1)(1.1s+1)100
待校正系统的开环幅频渐近特性曲线如下
L
′
(
ω
)
L'(omega)
L′(ω)所示:
校正后内系统的等效开环传递函数为:
G
k
(
s
)
=
G
1
(
s
)
G
2
(
s
)
1
+
G
1
(
s
)
G
2
(
s
)
H
(
s
)
=
100
s
(
0.0275
s
2
+
1.125
s
+
26
)
G_k(s)=frac{G_1(s)G_2(s)}{1+G_1(s)G_2(s)H(s)}=frac{100}{s(0.0275s^2+1.125s+26)}
Gk(s)=1+G1(s)G2(s)H(s)G1(s)G2(s)=s(0.0275s2+1.125s+26)100
校正后系统的开环幅频渐近特性曲线如下
L
′
′
(
ω
)
L''(omega)
L′′(ω)所示:
【开环幅频渐近特性曲线】
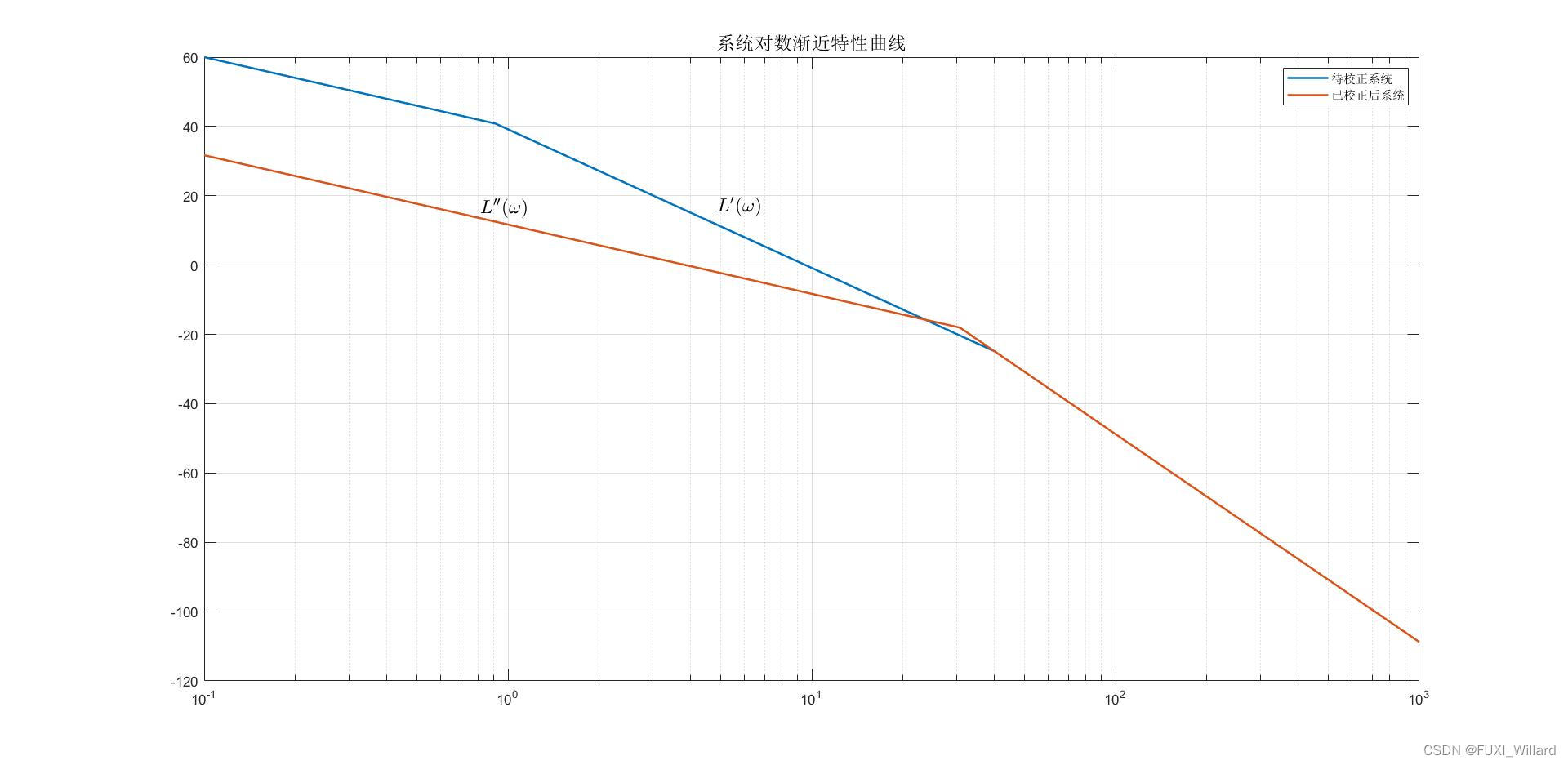
令
∣
G
k
(
j
ω
c
)
∣
=
1
|G_k({rm j}omega_c)|=1
∣Gk(jωc)∣=1,即
∣
10
ω
c
(
26
−
0.0275
ω
c
2
)
2
+
(
1.125
ω
c
)
2
∣
=
1
⇒
ω
c
=
3.85
r
a
d
/
s
left|frac{10}{omega_csqrt{(26-0.0275omega_c^2)^2+(1.125omega_c)^2}}right|=1Rightarrowomega_c=3.85{rm rad/s}
∣
∣ωc(26−0.0275ωc2)2+(1.125ωc)210∣
∣=1⇒ωc=3.85rad/s
校正后系统的相角裕度为:
γ
(
ω
c
)
=
90
°
−
arctan
1.125
ω
c
26
−
0.0275
ω
c
2
∣
ω
c
=
3.85
=
80.39
°
gamma(omega_c)=90°-left.arctanfrac{1.125omega_c}{26-0.0275omega_c^2}right|_{omega_c=3.85}=80.39°
γ(ωc)=90°−arctan26−0.0275ωc21.125ωc∣
∣ωc=3.85=80.39°
【已校正系统的Bode图】
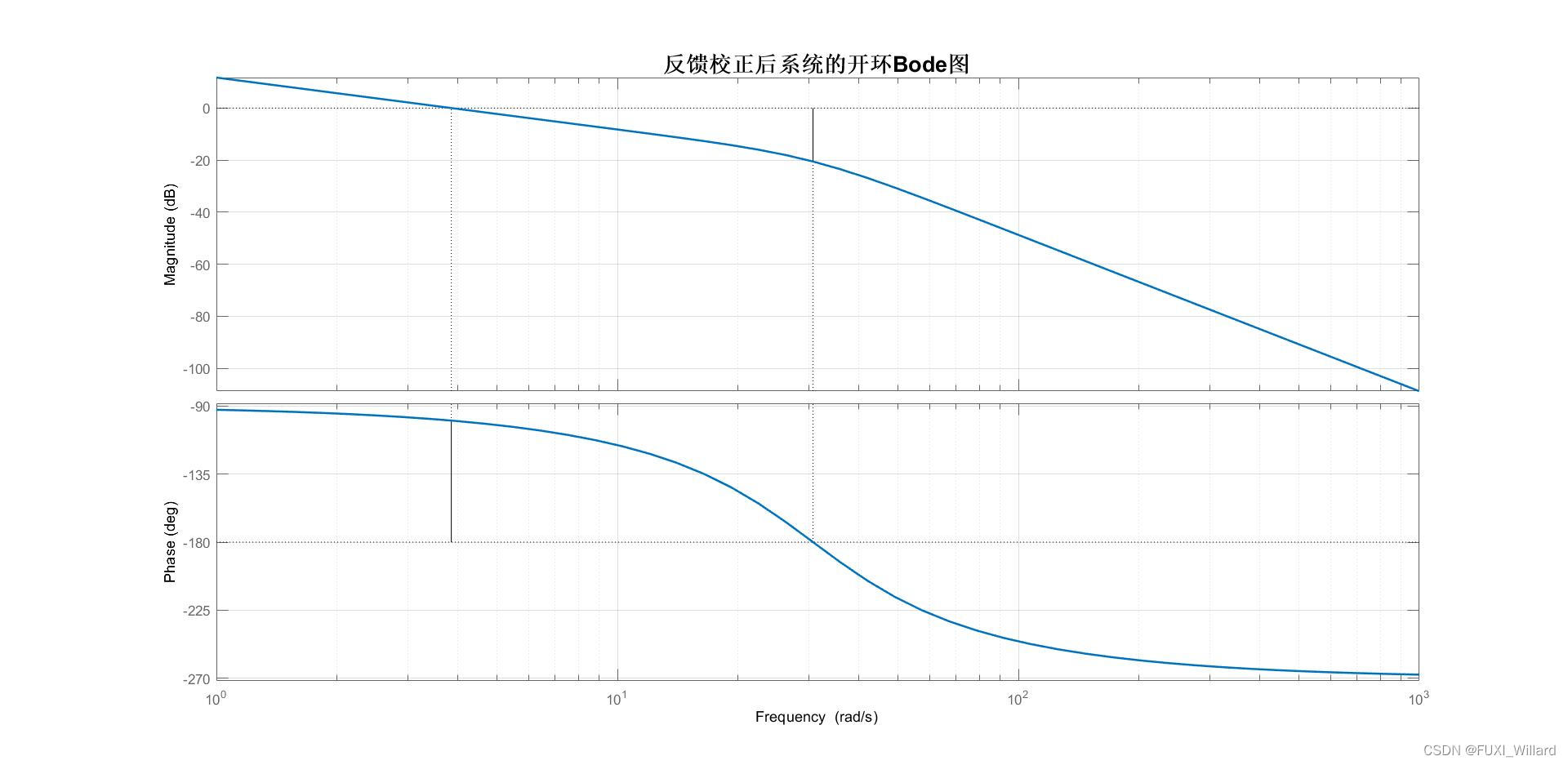
Example 6.10
设系统结构图如下图所示,要求采用串联校正和复合校正两种方法,消除系统跟踪斜坡输入信号的稳态误差,分别确定串联校正装置 G c ( s ) G_c(s) Gc(s)与复合校正前馈装置 G r ( s ) G_r(s) Gr(s)的传递函数.
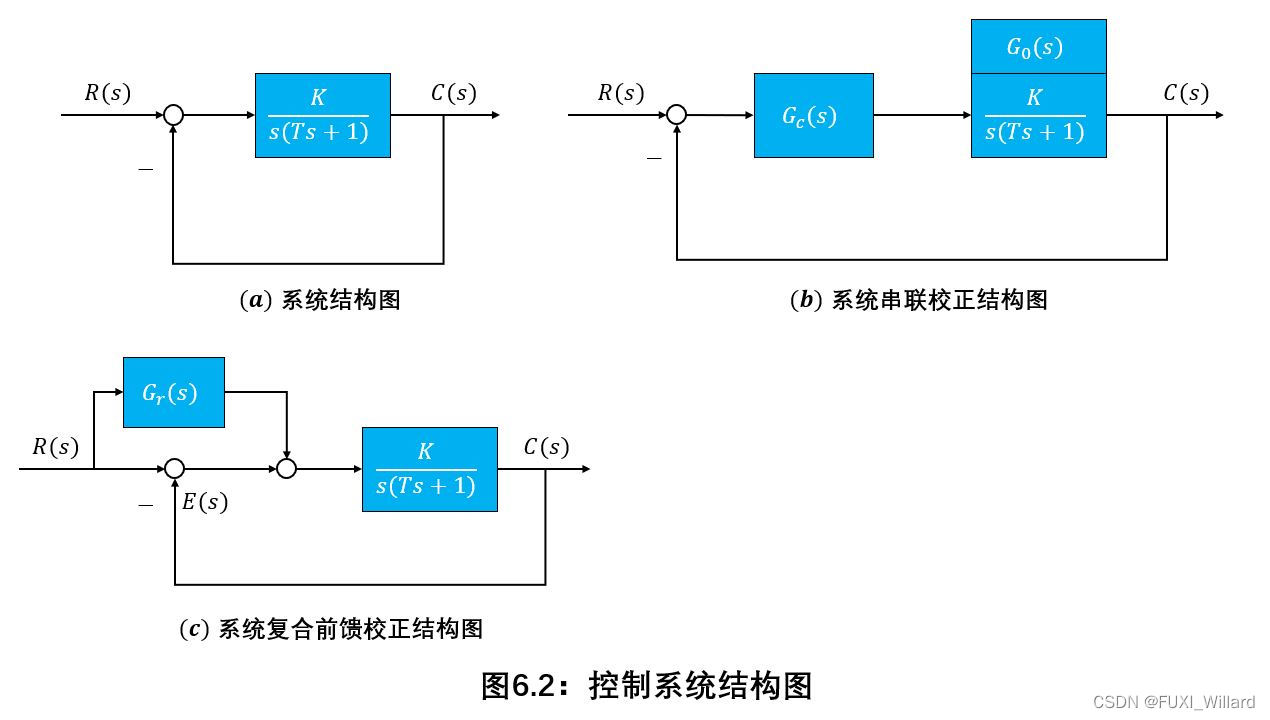
解:
【串联校正】
采用串联校正的结构图如图 b {rm b} b所示。
若使系统跟踪斜坡输入信号的稳态误差为零,则应取:
G
c
(
s
)
=
τ
s
+
1
s
G_c(s)=frac{tau{s}+1}{s}
Gc(s)=sτs+1
同时,必须保证闭环系统稳定.
校正后系统的开环传递函数为:
G
(
s
)
=
G
c
(
s
)
G
0
(
s
)
=
K
(
τ
s
+
1
)
s
2
(
T
s
+
1
)
G(s)=G_c(s)G_0(s)=frac{K(tau{s}+1)}{s^2(Ts+1)}
G(s)=Gc(s)G0(s)=s2(Ts+1)K(τs+1)
则校正后闭环系统的特征方程为:
D
(
s
)
=
T
s
3
+
s
2
+
K
τ
s
+
K
=
0
D(s)=Ts^3+s^2+Ktau{s}+K=0
D(s)=Ts3+s2+Kτs+K=0
若使系统稳定,则由劳斯判据可知,有:
K
τ
>
K
T
⇒
τ
>
T
Ktau>KTRightarrowtau>T
Kτ>KT⇒τ>T
【复合前馈校正】
采用复合前馈校正的结构图如图 c {rm c} c所示。
由图可得:
Φ
e
r
(
s
)
=
E
(
s
)
R
(
s
)
=
1
−
K
G
r
(
s
)
s
(
T
s
+
1
)
1
+
K
s
(
T
s
+
1
)
=
s
(
T
s
+
1
)
−
K
G
r
(
s
)
s
(
T
s
+
1
)
+
K
Phi_{er}(s)=frac{E(s)}{R(s)}=frac{1-displaystylefrac{KG_r(s)}{s(Ts+1)}}{1+displaystylefrac{K}{s(Ts+1)}}=frac{s(Ts+1)-KG_r(s)}{s(Ts+1)+K}
Φer(s)=R(s)E(s)=1+s(Ts+1)K1−s(Ts+1)KGr(s)=s(Ts+1)+Ks(Ts+1)−KGr(s)
由上式可知:当
K
>
0
,
T
>
0
K>0,T>0
K>0,T>0时,闭环系统稳定;
当输入信号为斜坡输入信号时,系统的稳态误差为:
e
s
s
(
∞
)
=
lim
s
→
0
s
E
(
s
)
=
lim
s
→
0
s
⋅
s
(
T
s
+
1
)
−
K
G
r
(
s
)
s
(
T
s
+
1
)
+
K
⋅
1
s
2
=
lim
s
→
0
s
(
T
s
+
1
)
−
K
G
r
(
s
)
s
[
s
(
T
s
+
1
)
+
K
]
e_{ss}(infty)=lim_{sto0}sE(s)=lim_{sto0}s·frac{s(Ts+1)-KG_r(s)}{s(Ts+1)+K}·frac{1}{s^2}=lim_{sto0}frac{s(Ts+1)-KG_r(s)}{s[s(Ts+1)+K]}
ess(∞)=s→0limsE(s)=s→0lims⋅s(Ts+1)+Ks(Ts+1)−KGr(s)⋅s21=s→0lims[s(Ts+1)+K]s(Ts+1)−KGr(s)
若使
e
s
s
(
∞
)
=
0
e_{ss}(infty)=0
ess(∞)=0,则有:
1
−
lim
s
→
0
K
G
r
(
s
)
s
=
0
⇒
G
r
(
s
)
=
s
K
1-lim_{sto0}frac{KG_r(s)}{s}=0Rightarrow{G_r(s)}=frac{s}{K}
1−s→0limsKGr(s)=0⇒Gr(s)=Ks
最后
以上就是幽默唇彩最近收集整理的关于Chapter6.1:线性系统的校正方法的全部内容,更多相关Chapter6.1:线性系统内容请搜索靠谱客的其他文章。








发表评论 取消回复