题目

题目链接

题意

在$Ox$轴上有一堆点，这些点有三种类型$R、B、P$型，现在要求添加一些线段把这些点连起来，使得如果去掉$R$类型点，剩下的点都是联通的。如果去掉$B$类型的点，剩下的点也是联通的,求最小的边长度总和。

题解

如果我们单单只看去掉$R(B)$类型的点的时候，这道题毫无疑问是一道最小生成树的题目，实际上也并不需要用一些最小生成树的做法来做，只需要按顺序扫一遍就好了。

但这个题不是，它要求这个图去掉$R(B)$类型的点之后，都仍旧是最小生成树。

我们称这张图为二树图(我胡起的，只是方便后面叙述，实际上并没有这个名字)。

那么如何构造这个二树图呢，我们采用归纳法。

我们从左向右扫描所得到的点，并且假设在所扫描过的点中已经过构造好了部分二树图。

那么对于我们当前正在扫描的点，该怎么进行处理呢？

1. 当前的点是$B(R)$点，那么我们需要把这个$B(R)$点与前面最近的$B(R)$点或者最近的$P$点相连接，这样的话保证了去掉$R(B)$点之后，当前的这个$B(R)$点连接到了生成树中，这样保持了二树图的性质。

2. 当前的点是$P$点，这种情况有点复杂，因为$P$点是不会被去掉的，所以$P$点影响了两种生成树。我们这样考虑，为了保证两个生成树都要连接到当前的这个$P$点，对于去掉$B(R)$点得到的生成树，想要连接$P$，那么我们一定要让这个$P$连接到最近的$R(B)$或者$P$点上，如果最近的是$P$点，那么直接连接就好了，因为$P$连接到了前面的$P$点上，那么这个$P$将同时连接到两颗生成树上去。
   而如果$P$到两颗树最近的点都不是$P$点（即上一个$P$与当前$P$点之间即有$B$点也有$R$点这种情况），我们首先让当前的$P$点连接最近的$B$点和最近的$R$点，在让当前的$P$点与前一个$P$点相连，这样的话，对于两颗生成树来说都产生了一个圈，为了保持生成树的性质，我们需要破圈。如果我们此时破了$P-P$边，那么获得优势是$cost(P_{now},P_{pre})$，保证是二树图，结束。如果我们不破$P-P$边，那么我们势必要在两个圈中各找一个最大的$B_x-B_{x+1}$和$R_y-R_{y+1}$破掉，获得优势$cost(B_x,B_{x+1})+cost(R_y,R_{y+1})$，保证是二树图，结束。因此我们比较那个优势大就选择那种破法。
   

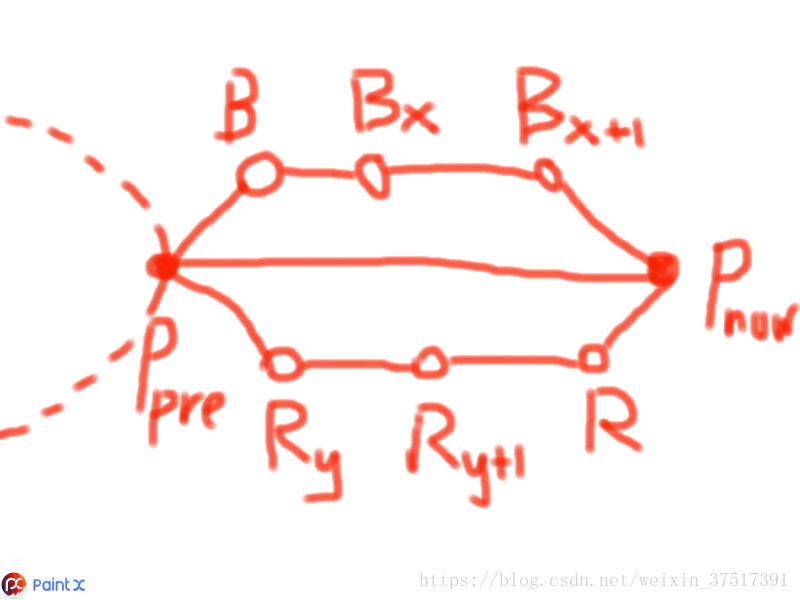
本题至此就解决了。

代码

#include <iostream>
#include <cstdio>
using namespace std;
const int maxn = 2e5+7;
typedef long long ll;
ll B,R,mxB,mxR,P,ans;
int n;
int main(){
    cin>>n;
    for(int i = 1;i <= n;++i){
        ll x;char c;
        scanf("%lld %c",&x,&c);
        x += 1e9+7;
        if(c == 'B'){
            if(B) ans += x - B,mxB = max(mxB,x - B);
            B = x;   
        }

        if(c == 'R'){
            if(R) ans += x - R,mxR = max(mxR,x - R);
            R = x;
        }

        if(c == 'P'){
            if(B) mxB = max(mxB,x - B),ans += x-B;
            if(R) mxR = max(mxR,x - R),ans += x-R;
            if(P) {
                ans += min(0ll,x - P - mxB - mxR);
            }

            B = R = P = x;
            mxB = mxR = 0;
        }
    }

    cout<<ans<<endl;
    return 0;
}

最后

以上就是幽默唇彩为你收集整理的codeforces 962E Byteland, Berland and Disputed Cities 最小生成树变形题目题意题解代码的全部内容，希望文章能够帮你解决codeforces 962E Byteland, Berland and Disputed Cities 最小生成树变形题目题意题解代码所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。