matplot画图控制marker点的个数_考研干货 | 北工大控制考研，第五章——频率特性知识总结...

阅读原文

01 频率特性

基本概念：

稳定的线性定常系统，其对正弦函数输入的稳态响应，称为频率响应。

输出与输入的振幅比，称为系统的幅频特性。它描述了系统对不同频率的正弦函数输入信号在稳态情况下的衰减(或放大)特性；输出与输入的相位差，称为系统的相频特性。

02 相关作图

（1） 极坐标图（奈奎斯特图）

在考研试题中,Nyquist曲线的绘制经常会遇到。在绘制过程中要把握好曲线的三个频段的绘制。

低频段：当w→0＋时,Nyquist曲线位于起点

对于最小相位系统

当系统中含有纯微分环节时,只要取v为负的微分环节的个数即可。

对于非最小相位系统，具体分析。

高频段：当w

时，Nyquist曲线位于终点。

当传递函数分子的阶次m小于分母的阶次n时，A(w)→0，终点位于坐标原点。

当n=m时，A(w)→常数。

中频段:

拐点：含有零点的个数就是系统凸凹变化的次数。

与实轴交点：使虚频V(w)=0的频率o，代入实频U(w)，即可得与实轴交点的横坐标。

与虚轴交点：使实频U(w)=0的频率o，代入虚频V(w），即可得与虚轴交点的纵坐标。

助记图：

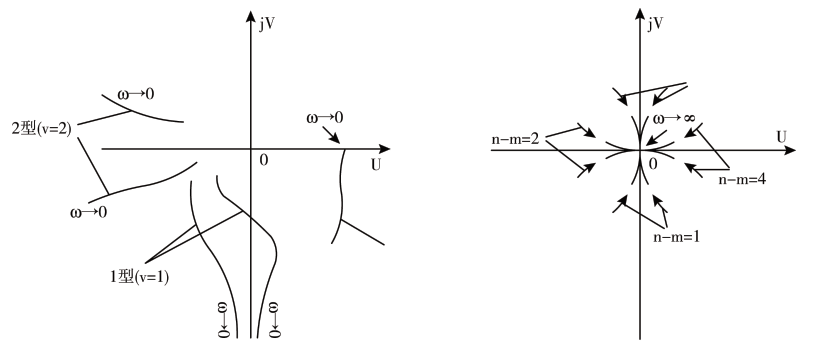
（2） 对数坐标图（伯德图）

课本169-178的典型环节要记忆清楚，深刻理解（画图基础）。

L（w）绘制：

把所有的转折频率标注在频率轴上；

绘制出低频渐近线，该直线斜率为-20vdB/dec(其中v为相应传递函数当中积分环节的个数)，点( o=1，L( a)=20lgK)在该段直线上，当最小的转折频率小于1时，该点在低频段的延长线上。

每经过一个转折频率斜率做相应的改变，斜率的改变取决于该转折频率所对应的典型环节的类型。

φ（w）绘制：先绘制出各环节的相频特性，然后再迭加。

03 稳定判据

（1）频域稳定性判据又称奈奎斯特（Nyquist）稳定性判据，简称奈氏判据。

给大家找了好理解的：

在对数相频特性中，当o增加时，若定义对数相频特性曲线从下向上穿越-180°线〔对应相角增加）为正穿越，从上向下穿越-180°线（对应相角减小）为负穿越，正、负穿越次数用N+、N_表示，则对数频率特性稳定判据为：在对数幅频特性曲线零分贝线以上的频率范围内，若对数相频特性曲线与-180°线的正负穿越数之差N=N+-N_，则Z= P-2N。Z 为零，表明系统稳定；Z不为零，表明系统不稳定，Z即为系统不稳定根的个数。

稳定裕度：

稳定裕度是衡量系统相对稳定性的指标，有相角裕度和幅值裕度。

（1）幅值裕度h

（2）相角裕度

博德图上的稳定判据:

可以在博德图上直接使用频域稳定性判据。如果系统是最小相位的，系统稳定的充要条件为：幅值裕度Lg> 0 dB；相位裕度

04 控制系统的开环频率特性分析

开环频率特性的“三频段”与系统性能之间的关系。

典型的开环对数幅频特性图如下：

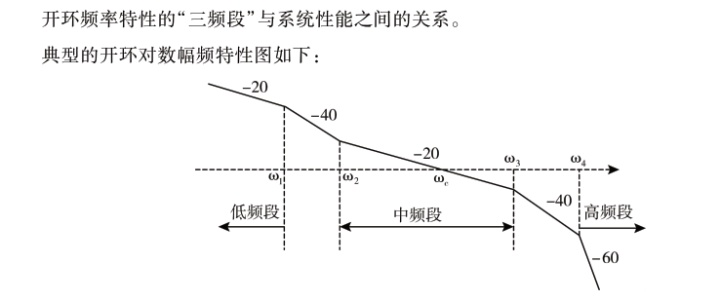
中频段宽度h。开环截止频率wc所对应的频率段其两端转折频率之比

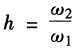
“三频段”与系统性能之间的关系:

低频段决定了系统的稳态精度，从提高稳态精度的角度，低频段越高(K越大)越陡(v越大)越好。

中频段决定了系统的动态性能，为获得良好的动态性能，应使y在30°~70°之间，L( w)应以–20的斜率穿过w轴，而且中频段应有足够的宽度。

高频段决定了系统抗高频干扰的能力。从提高抗干扰性能的角度，高频段越低越陡，抑制噪声的能力越强。