数字电路基础知识——组合逻辑电路之乘法器的设计（一）—— 并行、移位相加、加法树、查找表乘法器

数字电路基础知识——乘法器的设计（一）—— 并行、移位相加、加法树、查找表

乘法器的设计主要应用在数字信号处理和数字通信，本节主要介绍乘法器的四种实现方法。使用并行乘法器、移位相加乘法器、查找表乘法器、加法数乘法器。部分会涉及到寄存器时序逻辑电路。

乘法运算是由与、或、非等基本逻辑组合而成的，如下图所示是乘法器内部结构图：

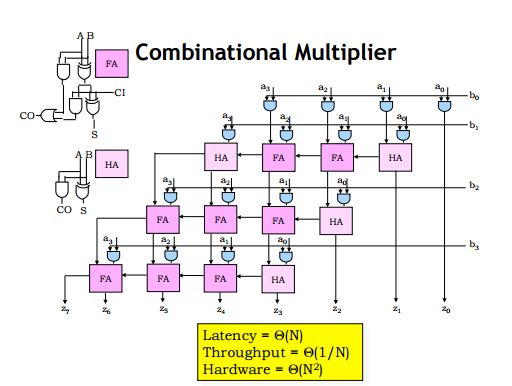
乘法器这种组合逻辑可以加流水线(pipeline),自己设计时就可以根据系统需要设置最优的流水线级数，让吞吐量，延时与cost平衡。在这篇博客中会提到流水线乘法器的实现。

一、并行乘法器

采用并行乘法设计的乘法器，在Verilog中直接采用 * 设计，这种方法设计出来的乘法器需要根据综合工具得到乘法结果，往往这种算法都是比较差的算法。
特点：
由乘法运算符描述、由EDA软件综合
运算速度快、耗用资源多
例：用Verilog实现八位并行乘法器

module multi(a,b,c);
parameter size = 8;
input [size-1:0] a,b;
output [2*size-1:0] c; 	//输出位宽

assign c = a*b;
endmodule

二、移位相加乘法器

1. 移位相加的原理
   从被乘数的最低位开始判断，若为1，则乘数左移i(i=0,1(width-1))位后，与上一次和进行相加，若为0，则乘数左移i位后，以0相加。直到被乘数的最高位。

   实际是由移位运算和加法运算构成。比较高速。

2. 优点：
   占用资源较少，主要在低速信号处理中

3. 缺点：
   串行乘法器的速度比较慢，一个结果输出需要更多的时钟周期。在高位宽的乘法运算中非常明显。

关键算法：

module multi_shift(a,b,c);  //不可综合提供算法
parameter size = 8;
input [size-1:0] a,b;
output [2*size-1:0] c; 	//输出位宽

reg[2*size-1:0] c;

integer i;
always@(a or b)
begin
	c=0;
	for (i=1; 1<=size;i=i+1) begin
		c = c + ((b[i] == 1)? (a<<[i-1]):0); 	//移位相加
	end
end
endmodule

三、查找表乘法器

1. 查找表乘法器原理：
   先将乘法的所有可能结果存储起来，然后将两个相乘的数据组合起来作为“地址”找到相应的结果。
   例如：
   设A,B为两个2位二进制数，则A,B各有4种取值可能，乘积有4*4=16种可能(排除重复的其实只有8种可能)，我们先将{A,B}对应的16种可能结果存储起来，然后对于每一特点的输入组合{A,B}，找到对应的输出即可。

2. 查找表乘法器特点：
   该方式速度很快，只取决于读取存储器的速度，但是预存结果要占用较多资源，因此是面积换取速度思想的体现。

   随着乘数位宽的增加，需要存储的结果迅速增加，不利于实现，因此该方式适用于位宽很小的情况。但是我们可以将高位宽的数据分解成低位宽的数据再调用查找表乘法器。

   适用情况：适合位数较小的乘法，特别适合有一个乘数为固定的乘法。

3. 设计思路
   对于四位查找表：
   A1 高两位, A2低两位
   
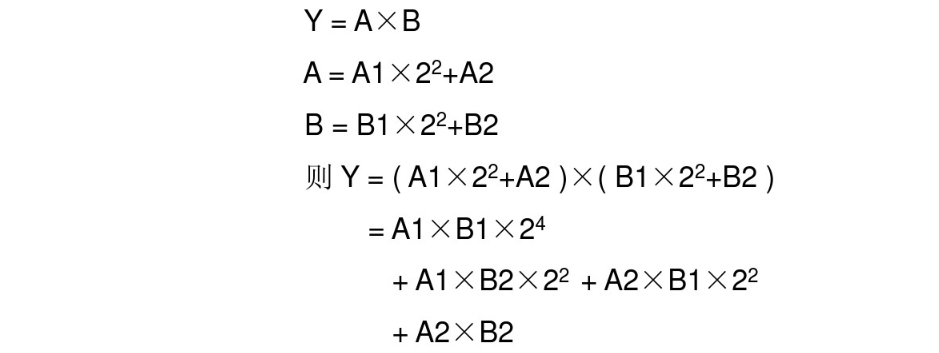
   对于八位查找表：
   A1 高四位, A2低四位
   

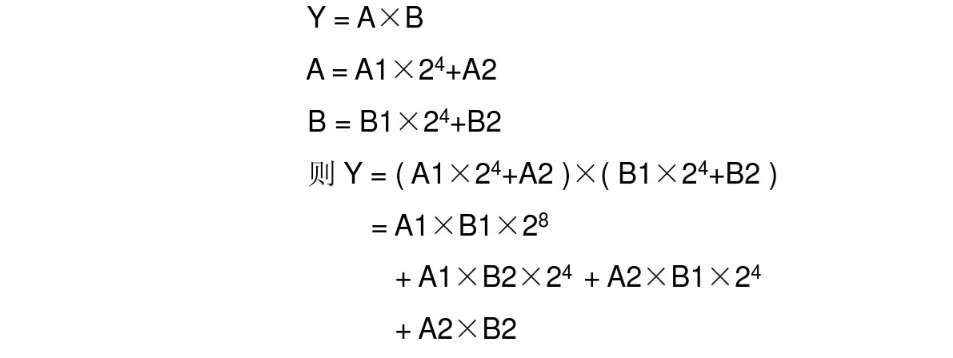
4. 下面一段代码是2位查找表乘法器:

module lookup22(dina,dinb,dout,clk);
input [1:0] dina,dinb;
input clk;
output [3:0] dout;
reg [3:0] dout;

always @ ( posedge clk )
begin
   case({dina,dinb})
      4'b0000:dout<=0;
      4'b0001:dout<=0;
      4'b0010:dout<=0;
      4'b0011:dout<=0;
      4'b0100:dout<=0;
      4'b0101:dout<=1;
      4'b0110:dout<=2;
      4'b0111:dout<=3;
      4'b1000:dout<=0;
      4'b1001:dout<=2;
      4'b1010:dout<=4;
      4'b1011:dout<=6;
      4'b1100:dout<=0;
      4'b1101:dout<=3;
      4'b1110:dout<=6;
      4'b1111:dout<=9;
      default: dout<=4'dx;
   endcase 
end   
endmodule

该乘法器计算两个2位数相乘只需要一个时钟周期。通过他们的组合，可以构成4位乘法器，代码如下：

5. 下面一段代码是通过上面的组合 4位查找表乘法器:

module lookup44(dina,dinb,dout,clk);
input [3:0] dina,dinb;
input clk;
output [7:0] dout;
reg [7:0] dout;

reg [1:0] a1,a2; 	//操作数高2位
reg [1:0] b1,b2;	//操作数低2位
wire [3:0] dout1,dout2,dout3,dout4;		//乘积每两位一组

//输入数据拆为高2位和低2位分别缓存
always @ ( posedge clk )
begin
   a1<=dina[3:2]; a2<=dina[1:0];
   b1<=dinb[3:2]; b2<=dinb[1:0];
end    

//调用2位查找表乘法器
lookup22 mul1(a1,b1,dout1,clk),
         mul2(a2,b1,dout2,clk),
         mul3(a1,b2,dout3,clk),
         mul4(a2,b2,dout4,clk);
         
//将4个乘法运算的结果相加输出
always @ ( posedge clk )
begin
   dout<=(dout1<<4)+(dout2<<2)+(dout3<<2)+dout4;
end  
endmodule

该乘法器计算两个数相乘需要2个时钟周期，在第1个上升沿装载一个数据，第2个上升沿调用查找表乘法器完成2位数相乘，第3个上升沿输出第一个结果，因此从输入到输出延迟2个时钟周期。同时在第2个上升沿会装载第二个数据，第3个上升沿会调用查找表乘法器完成2位数相乘，第4个上升沿输出第二个结果。

移位乘法器计算一个结果需要4个周期，该乘法器只需要2个周期，总时间还是少的多。

四、加法树乘法器

1. 加法树乘法器
   
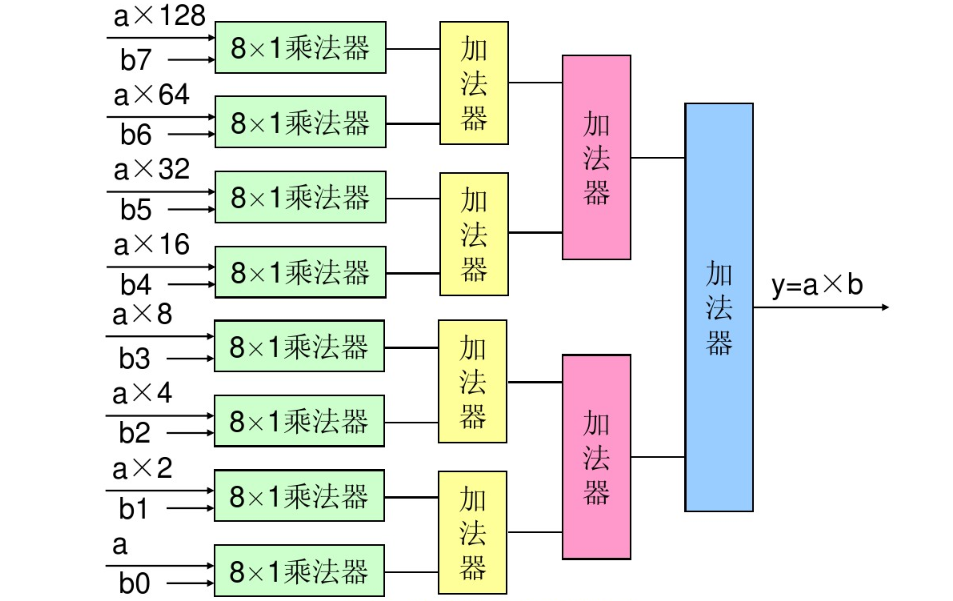
   能在一个时钟周期即可完成乘法运算。
2. 用Verilog实现8位加法树乘法器

module multi_add_tree(a,b,clk,out);
output [15:0] out;
input [7:0] a,b;
input clk;
wire [15:0] out;

wire [15:0] out1,c1;
wire [13:0] out2;
wire [11:0] out3.c2;
wire [9:0] out4;

reg [14:0] temp0; 
reg [13:0] temp1;
reg [12:0] temp2;
reg [11:0] temp3;
reg [10:0] temp4;
reg [9:0] temp5;
reg [8:0] temp6;
reg [7:0] temp7;

// 8*1乘法器

function [7:0] mut8_1;
input [7:0] operand;
input sel;

begin
	mut8_1 = sel ? operand : 8'b0000_0000;
end
endfunction 

//操作数b各位与操作数a相乘
always @(posedge clk)
begin
	temp7 = mut8_1(a,b[0]);
	temp6 = (mut8_1(a,b[1]))<<1;
	temp5 = (mut8_1(a,b[2]))<<2;
	temp4 = (mut8_1(a,b[3]))<<3;
	temp3 = (mut8_1(a,b[4]))<<4;
	temp2 = (mut8_1(a,b[5]))<<5;
	temp1 = (mut8_1(a,b[6]))<<6;
	temp0 = (mut8_1(a,b[7]))<<7;
end

//加法树运算
assign out1 = temp0 + temp1;
assign out2 = temp2 + temp3;
assign out3 = temp4 + temp5;
assign out4 = temp6 + temp7;
assign c1 = out1 + out2;
assign c1 = out3 + out4;
assign out = c1 + c2;

endmodule

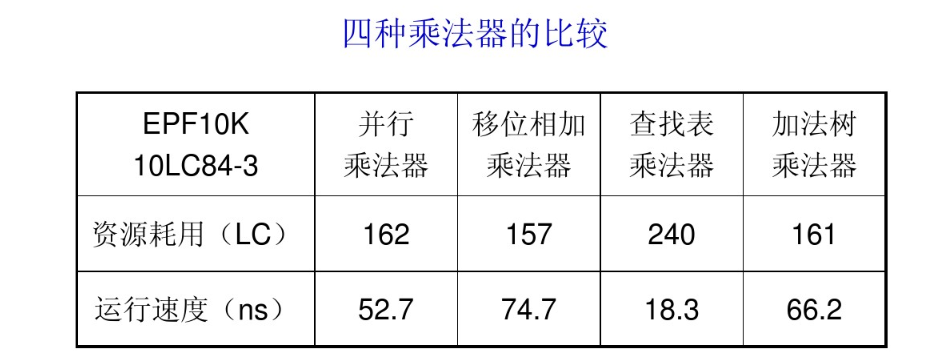
五、四种乘法器比较

四种乘法器资源好用和运行速度的比较：

六、乘累加器

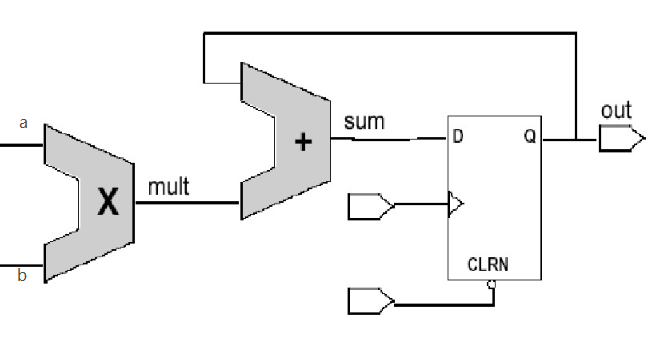
八位乘累加器的实现：即一个时钟实现一次乘法运算，然第二个时钟在实现一次乘法运算，最后将结果累加构成乘累加器。

module MAC(a, b, out, clk, clr);
output [15:0] out;
input [7:0] a, b;
input clk, clr;
wire [15:0] sum;
reg [15:0] out;

function [15:0] mult;
input [7：0] a,b;
reg [15:0] result;
integer i;
begin
	result = a[0]? b :0;
	for (i=1; i<= 7;i=i+1)
		begin
		 result = result + ((a[i] == 1)?  (b<<(i-1)): 0); 	//移位相加
		end
	mult = result;
end
endfunction

assign sum = mult(a,b) + out;

always@(posedge clk or posedge clr)
begin
	if(clr) out <= 0;
	else out <= sum;
end

endmodule

最后

以上就是热情汉堡为你收集整理的数字电路基础知识——组合逻辑电路之乘法器的设计（一）—— 并行、移位相加、加法树、查找表乘法器的全部内容，希望文章能够帮你解决数字电路基础知识——组合逻辑电路之乘法器的设计（一）—— 并行、移位相加、加法树、查找表乘法器所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。