目录
一、题目要求
二、数据集介绍
三、Logistics回归模型
3.1 Logistics回归模型介绍
3.2 Logistics回归算法原理
3.3 Logistics回归算法核心代码解释
1. 定义Sigmoid函数
2. 梯度下降法求解logistics回归权重W
3. 结果预测函数
4. 数据可视化处理
3.4 Logistics回归结果
四、对率回归模型的检验
4.1 乳腺癌“breast_cancer”数据集测试
4.2 糖尿病“Diabetes”数据集测试
五、线性判别分析
六、运行结果
七、附件
一、题目要求
3.3 编程实现对率回归,并给出西瓜数据集3.0α上的结果
3.4 选择两个 UCI 数据集,比较 10 折交叉验证法和留一法所估计出的对率回归的错误率。
3.5 编辑实现线性判别分析,并给出西瓜数据集 3.0α 上的结果.
二、数据集介绍
本次实验使用到三个数据集,分别是西瓜数据集3.0α ,UCI分类数据集中的糖尿病数据集“Diabetes.xls”和乳腺癌数据集“breast_cancer.csv”。
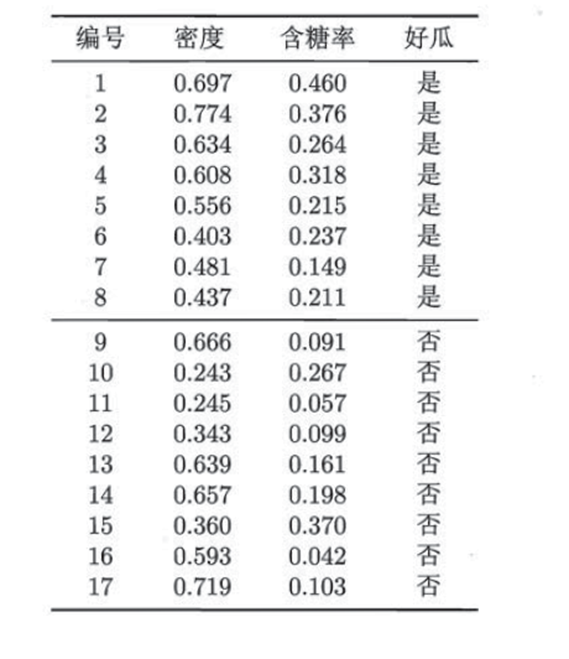
西瓜数据集3.0α包含17条信息,每条信息对应西瓜的2种属性,给出了该西瓜是否为好瓜,“是”表示该西瓜是好瓜,“否”表该西瓜不是好瓜。西瓜数据集3.0α的具体内容如下图所示。
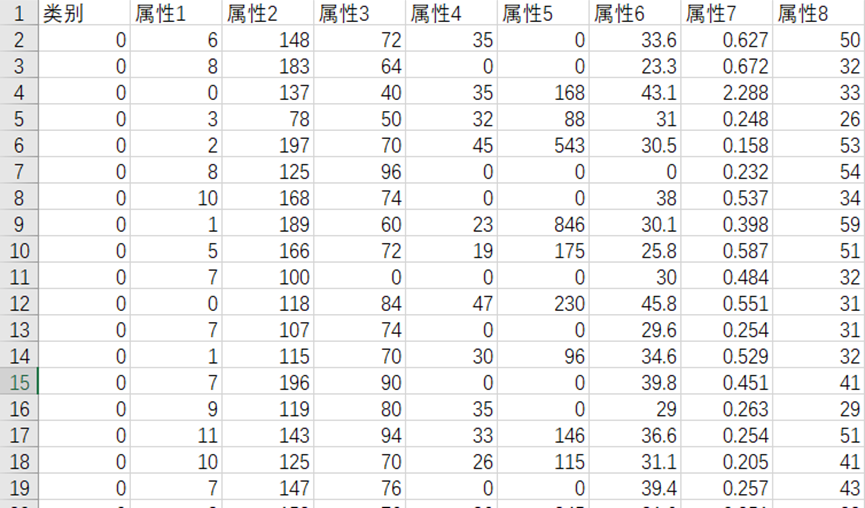
糖尿病“Diabetes”数据集共包含768条信息,每条信息对应一位可能患有糖尿病的患者的8个属性,并给出了该患者是否患有糖尿病的结果,“1”表示该患者确实患有糖尿病,“0”表该患者不患有糖尿病。“Diabetes”数据集的具体内容如下图所示。
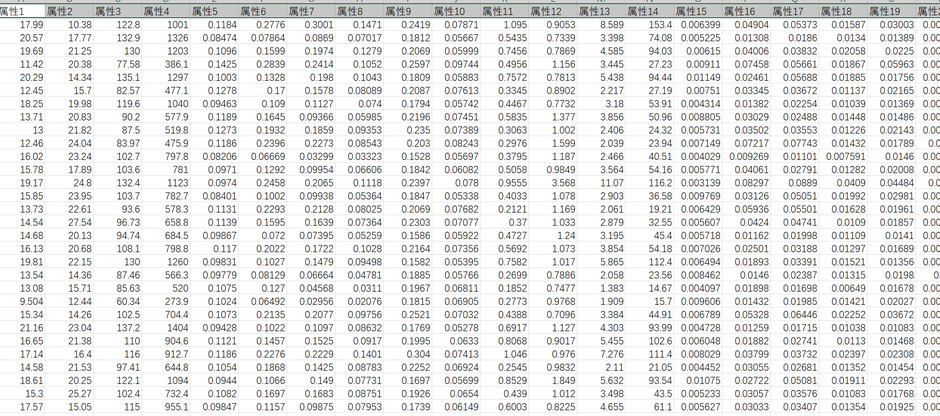
乳腺癌“breast_cancer”数据集共包含568条信息,每条信息对应一位可能患有乳腺癌的患者的30个属性,并给出了该患者是否患有乳腺癌的结果,“1”表示该患者确实患有乳腺癌,“0”表该患者不患有乳腺癌。乳腺癌“breast_cancer”数据集的具体内容如下所示:
三、Logistics回归模型
3.1 Logistics回归模型介绍
Logistic Regression是经典的分类模型,常用于二分类。Logistics回归可以认为是一个被Sigmoid函数(logistic方程)所归一化后的线性回归模型。Logistic 回归的本质是:假设数据服从这个分布,然后使用极大似然估计做参数的估计。
3.2 Logistics回归算法原理
Logistic函数(或称为Sigmoid函数),函数形式为:
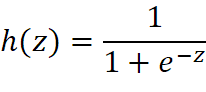
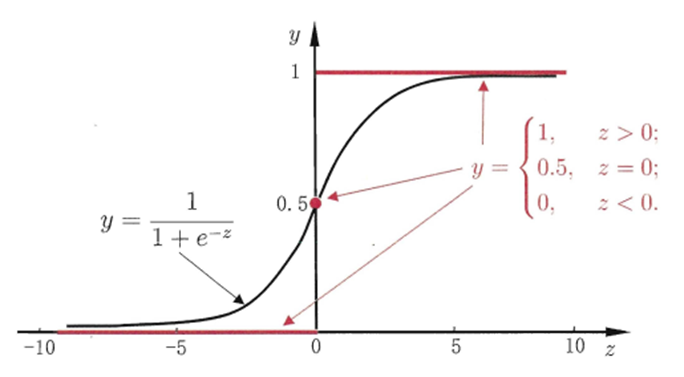
对于线性边界的情况,边界形式如下:
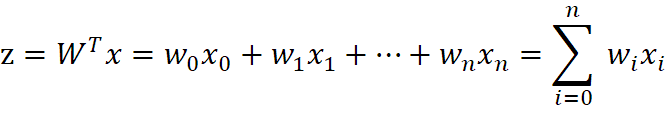
其中,训练数据为向量![]() ,最佳参数
,最佳参数![]() ,构造预测函数为:
,构造预测函数为:
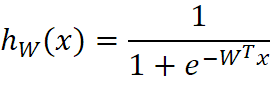
基于最大似然估计推导得到代价函数J:
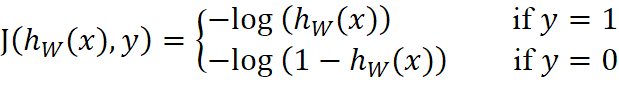
构造整体代价函数Cost为:
![]()
使用梯度下降法求解Cost的最优解:
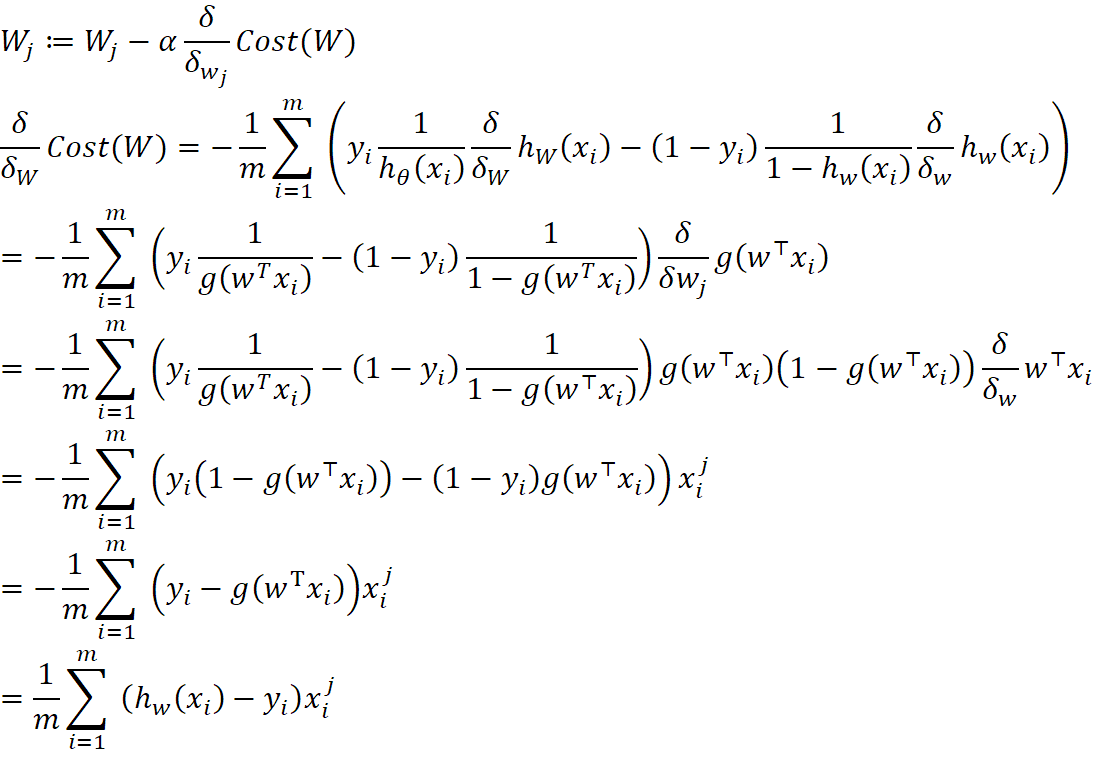
梯度下降法算法流程:
- 初始化W
- 更新W:
- 迭代达到一定的次数或一定阈值
3.3 Logistics回归算法核心代码解释
1. 定义Sigmoid函数
def sigmoid(x, W):
return 1.0 / (1.0 + np.exp(-x * W))
2. 梯度下降法求解logistics回归权重W
# logistics回归,返回W权重
def logistic_regression(train_X, labels, alpha=0.01, max_iter=1001):
X = np.mat(train_X)
Y = np.mat(labels).T # 转置为列向量
m, n = np.shape(X)
# 随机初始化W
W = np.mat(np.random.randn(n, 1))
# 更新W
for i in range(max_iter):
H = sigmoid(X, W)
dW = X.T * (H - Y) # dW:(3,1)根据梯度下降算法,需要先求得dCost/dW,此处用dW代替
W -= alpha * dW # 梯度下降 W = W - alpha*dCost/dW
return W
在梯度下降法求解logistics回归权重W的函数中,我们将训练集train_X和真实分类情况labels进行了矩阵化处理,得到X,Y矩阵。注意此时X矩阵为X=[X, 1],即为X多添加了一列全1列向量,方便![]() 计算,如下所示。
计算,如下所示。
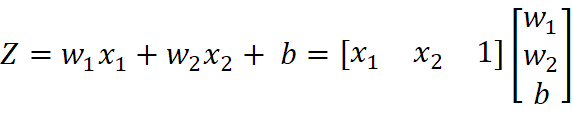
W更新部分的代码参照梯度下降法推导的公式![]() 编写,
编写,![]() ,推广到矩阵形式即为
,推广到矩阵形式即为
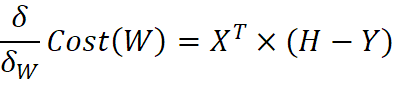
最后函数返回W即为logistics回归模型的W参数。
3. 结果预测函数
# 结果输出函数
def predict(X, W):
m = len(X)
pred = np.zeros(m)
for i in range(m):
if sigmoid(X[i], W) > 0.5: # 使用sigmoid判断,大于0.5label为1,否则为0
pred[i] = 1
return pred
将训练好的模型参数W和测试集X输入到函数,根据sigmoid函数进行划分,大于0.5为1,否则为0,可以输出预测结果。
4. 数据可视化处理
# 数据可视化
def show_diagram(train_X, labels, W):
w1 = W[0, 0]
w2 = W[1, 0]
b = W[2, 0]
plot_x1 = np.arange(0, 1, 0.01)
plot_x2 = -w1 / w2 * plot_x1 - b / w2
plt.plot(plot_x1, plot_x2, c='r', label='decision boundary')
plt.title('watermelon_3a')
plt.xlabel('density')
plt.ylabel('ratio_sugar')
plt.scatter(train_X[labels == 0, 0].A, train_X[labels == 0, 1].A, marker='^', color='r', s=80, label='bad')
plt.scatter(train_X[labels == 1, 0].A, train_X[labels == 1, 1].A, marker='o', color='g', s=80, label='good')
plt.legend(loc='upper right')
plt.show()
根据数据集绘制散点图,并根据分类模型的结果绘制决策边界,![]() ,上式中x1对应于横坐标,x2对用于纵坐标,决策边界z=0,因此得到直线方程是:
,上式中x1对应于横坐标,x2对用于纵坐标,决策边界z=0,因此得到直线方程是:
![]()
![]()
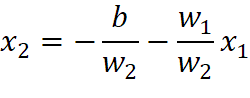
3.4 Logistics回归结果
输出可视化图形:
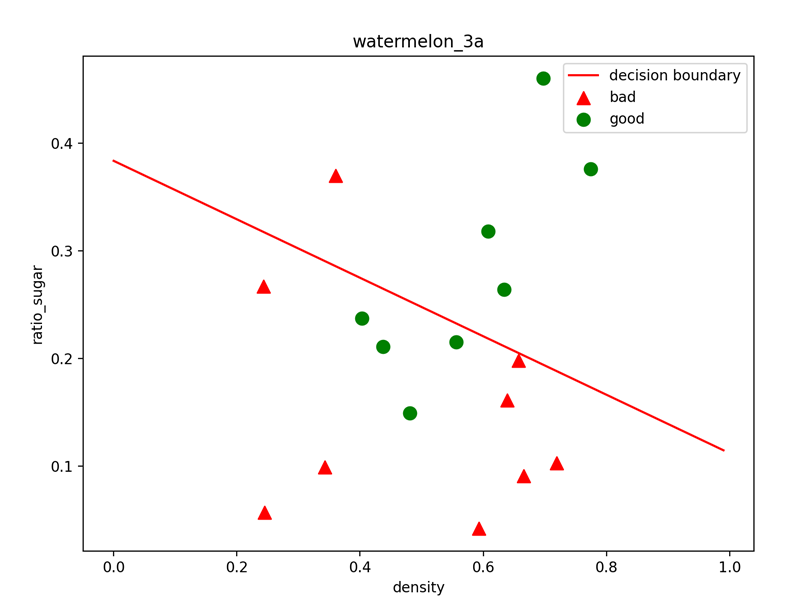
可以看到,绿色代表good,红色代表bad,经过决策边界划分后,区域被分为两部分,代表二分类结果。
输出结果部分:
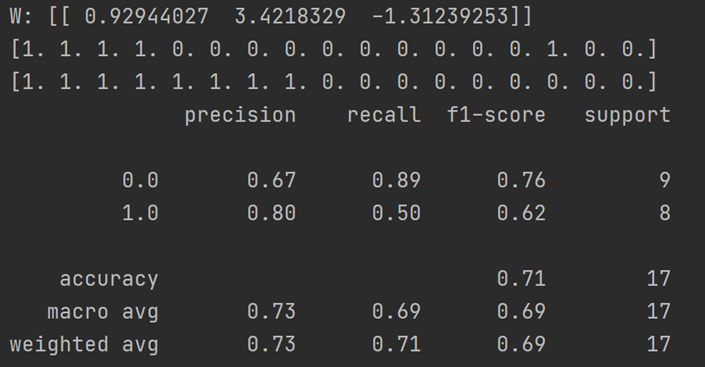
logistics回归最终的输出结果,前两行分别为预测结果和真实结果,下面为二分类的性能评估,准确率在71%,梯度下降模型做的还不够完美,如果使用随机梯度下降的话,结果可能会更好一些。
四、对率回归模型的检验
选择两个UCI数据集,比较10折交叉验证法和留一法所估计的对率回归的错误率。
10折交叉验证法函数:
1. def K_fold(train_X, labels, splits=10):
2. order_id = []
3. total_acc = 0
4. sfolder = StratifiedKFold(n_splits=splits, shuffle=True) # 十折交叉验证划分数据集
5. for num, (train, test) in enumerate(sfolder.split(train_X, labels)):
6. x_train = train_X[train, :]
7. y_train = labels[train]
8. x_test = train_X[test, :]
9. y_test = labels[test]
10. order_id.extend(test)
11.
12. # 开始进行logistics回归分类训练
13. W = logistics.logistic_regression(x_train, y_train, alpha=0.01, max_iter=1001) # 计算权重W
14. y_pred = logistics.predict(x_test, W) # 根据训练好的模型进行预测并输出预测值
15.
16. acc = accuracy_score(y_test, y_pred)
17. total_acc += acc
18. print('第', num + 1, '折验证的错误率', 1 - acc)
19. print("十折交叉验证的平均错误率为:", 1 - total_acc / splits)
这部分算法在上次博客中已经详细解释过,在本部分不再赘述。
留一法函数:
def leave_one(train_X, labels):
loo = LeaveOneOut()
total_acc = 0
loo.get_n_splits(train_X)
num = 0
for train_index, test_index in loo.split(train_X, labels):
x_train, x_test = train_X[train_index], train_X[test_index]
y_train, y_test = labels[train_index], labels[test_index]
# 开始进行logistics回归分类训练
W = logistics.logistic_regression(x_train, y_train, alpha=0.01, max_iter=1001) # 计算权重W
y_pred = logistics.predict(x_test, W) # 根据训练好的模型进行预测并输出预测值
acc = accuracy_score(y_test, y_pred)
total_acc += acc
num += 1
if num % 100 == 0:
print("前", num, "组错误率为", 1 - (total_acc / num))
print("留一法的平均错误率为:", 1 - (total_acc / num))
如果数据集D的大小为N,那么用N-1条数据进行训练,用剩下的一条数据作为验证。用一条数据作为验证的坏处就是可能Eval 和Eout 相差很大,所以在留一交叉验证里,每次从D中取一组作为验证集,直到所有样本都作过验证集,共计算N次,最后对验证误差求平均,这种方法称之为留一法交叉验证。
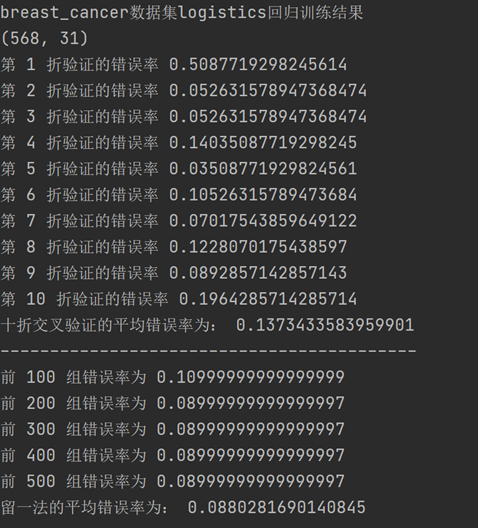
4.1 乳腺癌“breast_cancer”数据集测试
带入logistics回归模型后得到的10折交叉验证法和留一法所估计的对率回归的错误率结果输出如下:
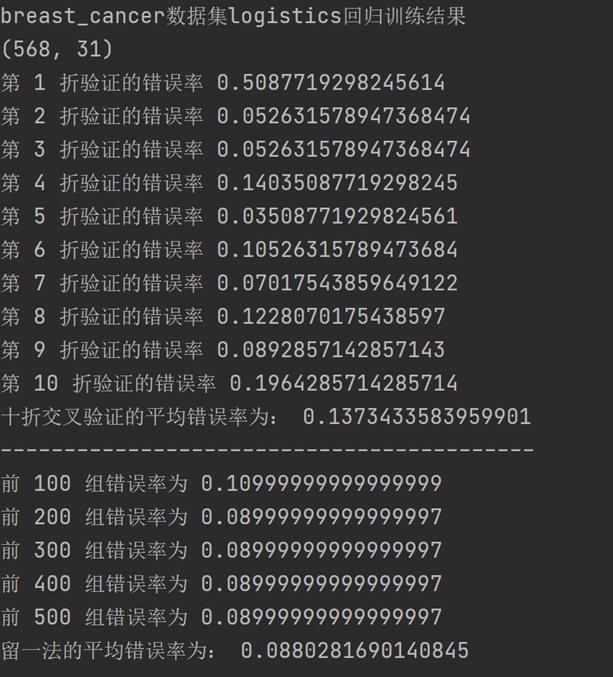
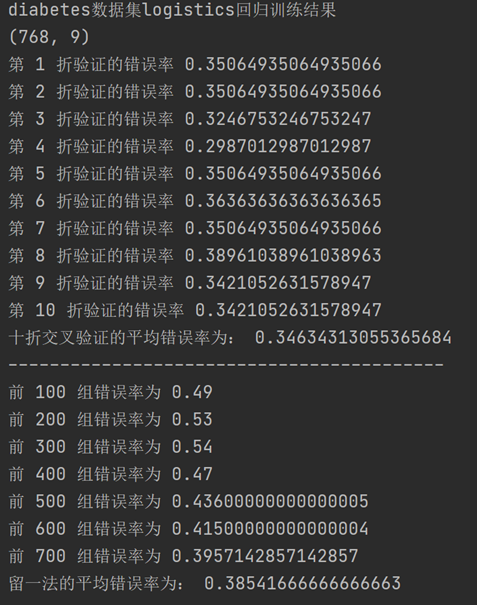
4.2 糖尿病“Diabetes”数据集测试
带入logistics回归模型后得到的10折交叉验证法和留一法所估计的对率回归的错误率结果输出如下:
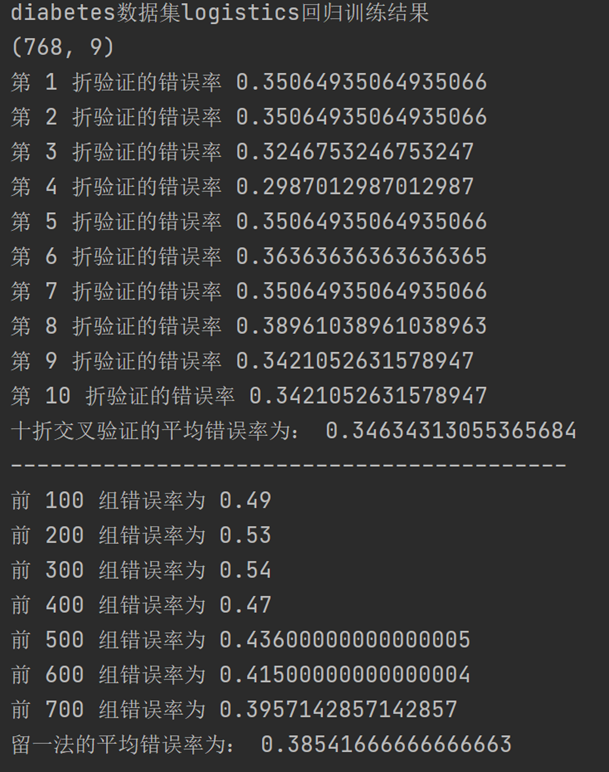
五、线性判别分析
线性判别分析是一种经典的线性学习方法,亦称“Fisher判别分析”。LDA的思想较为朴素:给定训练样例集,设法将阳历投影到一条直线上,使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离;在队新样本进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来确定新样本的类别。
给定数据集![]() ,令
,令![]() 分别表示第
分别表示第![]() 类示例的集合、均值向量、协方差矩阵。若将数据投影到直线w上,则两类样本的中心在直线上的投影分别为wTμ0和wTμ1;若将所有样本点都投影到直线上,则两类样本的协方差分别为
类示例的集合、均值向量、协方差矩阵。若将数据投影到直线w上,则两类样本的中心在直线上的投影分别为wTμ0和wTμ1;若将所有样本点都投影到直线上,则两类样本的协方差分别为![]() 和
和![]() 。由于直线式一维空间,因此
。由于直线式一维空间,因此![]() 和
和 ![]() 均为试数。
均为试数。
故最大化目标
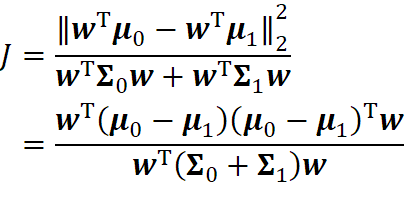
定义“类内散度矩阵”
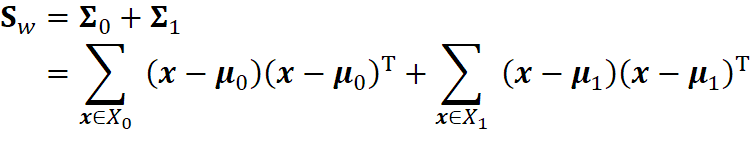
以及“类间散度矩阵”
![]()
结合“拉格朗日乘子法”,可得
![]()
在代码实现的过程中
mean1 = np.array([np.mean(x1[:, 0]), np.mean(x1[:, 1])])
mean2 = np.array([np.mean(x2[:, 0]), np.mean(x2[:, 1])])
Sw = np.zeros((2, 2))
for i in range(x1.shape[0]):
Sw = calculate(Sw, x1[i, :] - mean1)
for i in range(x2.shape[0]):
Sw = calculate(Sw, x2[i, :] - mean2)
w = np.linalg.inv(Sw) @ (mean1 - mean2).transpose()
变量mean1和mean2则表示两类样例的均值向量,Sw则表示计算出的“类间散度矩阵,进而就计算出矩阵系数向量w。由于我们仅关心样例点投影到直线后的投影点直接的距离关系,所以只计算出一条过原点的直线,直线沿垂直方向移动并不影响投影结果。
六、运行结果
3.3 编程实现对率回归,并给出西瓜数据集3.0α上的结果
输出可视化图形:
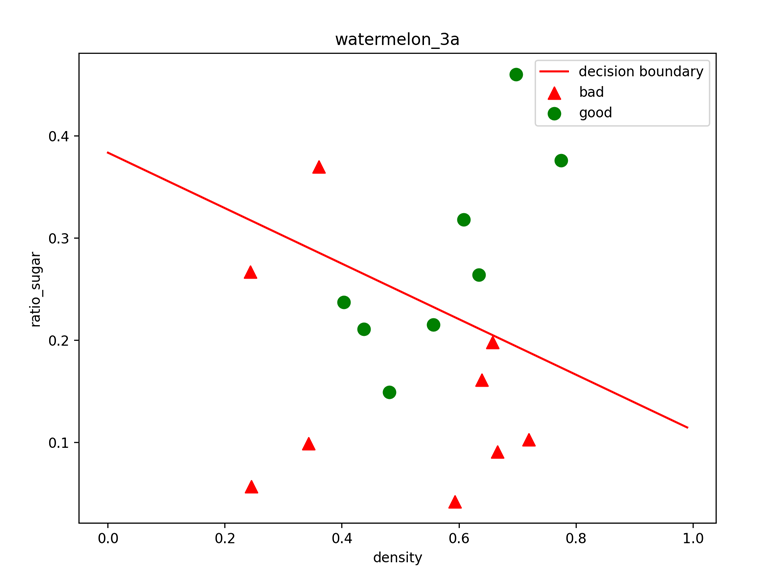
可以看到,绿色代表good,红色代表bad,经过决策边界划分后,区域被分为两部分,代表二分类结果。
输出结果部分:
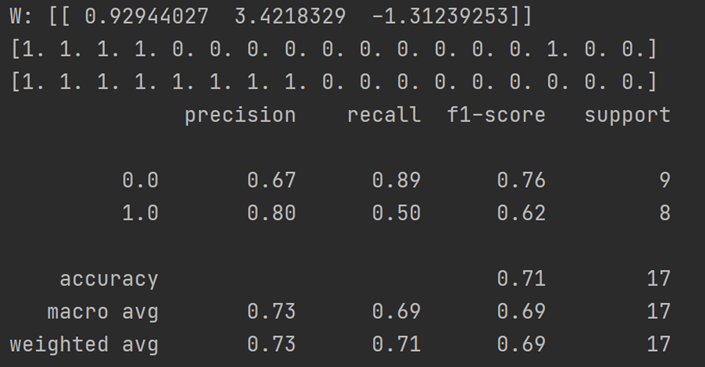
3.4 选择两个 UCI 数据集,比较 10 折交叉验证法和留一法所估计出的对率回归的错误率。
将UCI乳腺癌数据集带入logistics回归模型后得到的10折交叉验证法和留一法所估计的对率回归的错误率结果输出如下:
将UCI糖尿病数据集带入logistics回归模型后得到的10折交叉验证法和留一法所估计的对率回归的错误率结果输出如下:
3.5 编辑实现线性判别分析,并给出西瓜数据集 3.0α 上的结果.
线性判别分析结果为:
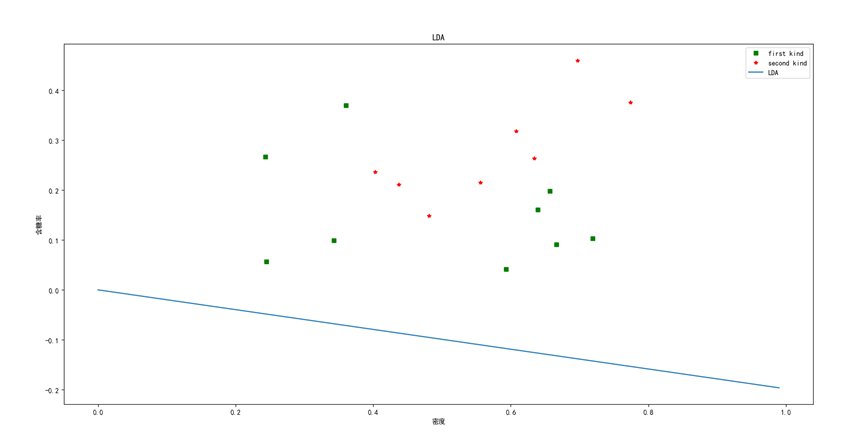
线性判别分析的直线为:
![]()
由线性判别分析结果图可以看出,该数据集使用“线性判别分析”进行降维的结果并不理想。
七、附件(见我的资源)
1. 习题3.3代码
2.习题3.4代码
3.习题3.5代码
最后
以上就是热情汉堡最近收集整理的关于西瓜书学习笔记---第三章 线性模型一、题目要求二、数据集介绍三、Logistics回归模型四、对率回归模型的检验五、线性判别分析六、运行结果七、附件(见我的资源)的全部内容,更多相关西瓜书学习笔记---第三章内容请搜索靠谱客的其他文章。








发表评论 取消回复