二阶系统阶跃响应实验_控制系统动态特性的计算以及阶跃响应波德图等

初始化       

已知开环传递函数       

求其单位负反馈的闭环传递函数       

闭环传递函数的分子       

闭环传递函数的分母       

常数K(学过控制工程的知道其含义

峰值时间tp 

超调量Mp 

上升时间tr

调节时间ts，%2的误差带 

阶跃响应

PD调节

PD调节后的阶跃响应

PD调节后的传递函数的分子

PD调节后的传递函数的分母

PD调节后的传递函数的K

PD调节后的峰值时间

PD调节后的超调量

PD调节后的调节时间 

PD调节后的阶跃响应 

伯德图

初始化

clc
clear

已知开环传递函数

Gs=tf([40*40],[1 0.6*40 40*40]);

求其单位负反馈的闭环传递函数

G=feedback(Gs,1);
figure(1)

闭环传递函数的分子

num=cell2mat(G.num);

闭环传递函数的分母

den=cell2mat(G.den);

常数K(学过控制工程的知道其含义)

finalvalue=polyval(num,0)/polyval(den,0); %y(∞)=lim sY(s)=limG(s)
[y,t]=step(G);
[yp,k]=max(y);

峰值时间tp

tp=t(k);

超调量Mp

Mp=100*(yp-finalvalue)/finalvalue;

上升时间tr

for i=1:length(y)if y(i)>finalvalue
        tr=(t(i)+t(i-1))/2;breakendend

调节时间ts，%2的误差带

len=length(t);while (y(len)>0.98*finalvalue)&(y(len)<1.02*finalvalue)< span="">
    len=len-1;end;
ts=t(len);

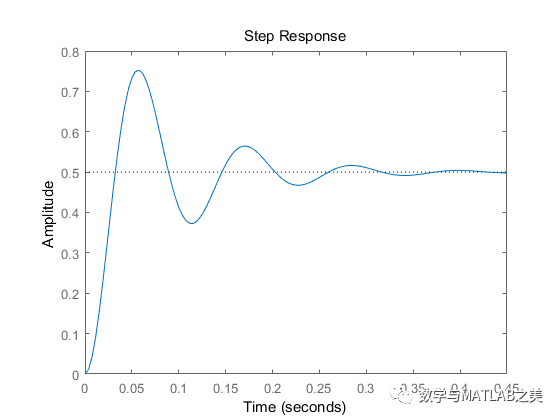
阶跃响应

step(G)
disp(['PD调节前系统的上升时间：tr=',num2str(tr)])
disp(['PD调节前系统的调节时间：ts=',num2str(ts)])
disp(['PD调节前系统的峰值时间：tp=',num2str(tp)])
disp(['PD调节前系统的超调量：{sigma}%=',num2str(Mp)])

PD调节前系统的上升时间：tr=0.03262
PD调节前系统的调节时间：ts=0.29934
PD调节前系统的峰值时间：tp=0.057565
PD调节前系统的超调量：{sigma}%=50.5194

PD调节

Gs=tf([40*40],[1 0.6*40 40*40]);
Gs1=tf([0.01 0],[1])+1;%Gs1=0.01s+1
Gs2=Gs*Gs1;
G=feedback(Gs2,1);
hold on

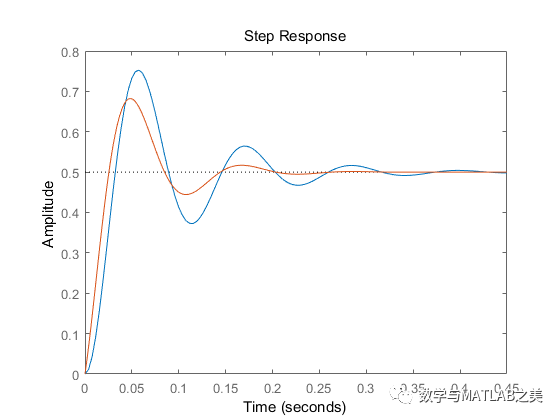
PD调节后的阶跃响应

step(G);

PD调节后的传递函数的分子

num=cell2mat(G.num);

PD调节后的传递函数的分母

den=cell2mat(G.den);

PD调节后的传递函数的K

finalvalue=polyval(num,0)/polyval(den,0); %y(∞)=lim sY(s)=limG(s)
[y,t]=step(G);
[yp,k]=max(y);

PD调节后的峰值时间

tp=t(k); % G(s)=Y(s)/(1/s)=sY(s)

PD调节后的超调量

Mp=100*(yp-finalvalue)/finalvalue;for i=1:length(y)if y(i)>finalvalue
        tr=(t(i)+t(i-1))/2;breakendend

PD调节后的调节时间

len=length(t);while (y(len)>0.98*finalvalue)&(y(len)<1.02*finalvalue)< span="">
    len=len-1;end;
ts=t(len);

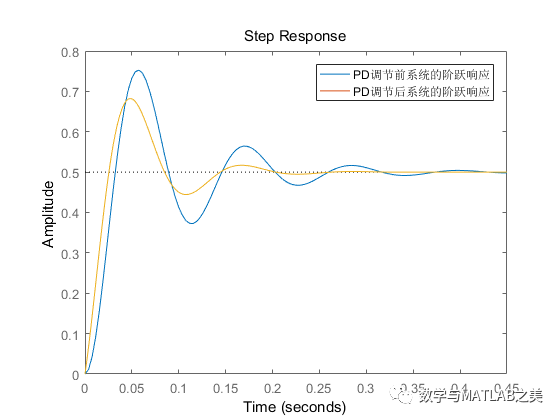
PD调节后的阶跃响应

step(G)
fprintf('n')
disp(['PD调节后系统的上升时间：tr=',num2str(tr)])
disp(['PD调节后系统的调节时间：ts=',num2str(ts)])
disp(['PD调节后系统的峰值时间：tp=',num2str(tp)])
disp(['PD调节后系统的超调量：{sigma}%=',num2str(Mp)])
legend('PD调节前系统的阶跃响应','PD调节后系统的阶跃响应')

PD调节后系统的上升时间：tr=0.02648
PD调节后系统的调节时间：ts=0.18421
PD调节后系统的峰值时间：tp=0.048354
PD调节后系统的超调量：{sigma}%=36.4864

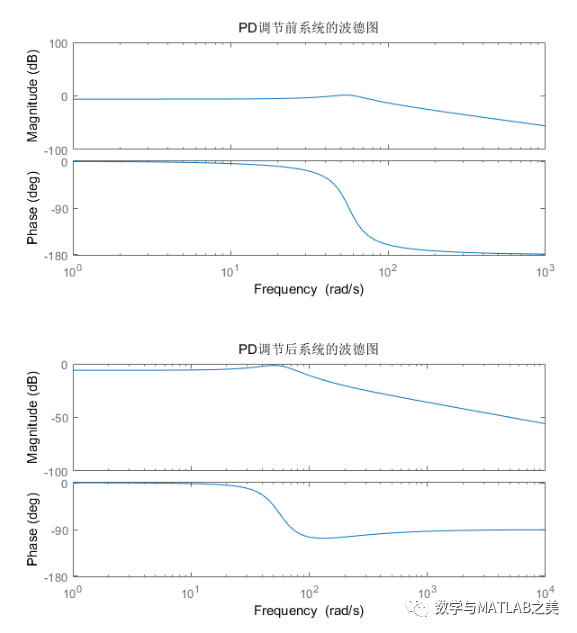
伯德图

figure(2)
subplot(2,1,1)
Gs=tf([40*40],[1 0.6*40 40*40]);
G=feedback(Gs,1);
bode(G)
title('PD调节前系统的波德图')
Gs=tf([40*40],[1 0.6*40 40*40]);
Gs1=tf([0.01 0],[1])+1;
Gs2=Gs*Gs1;
G=feedback(Gs2,1);
hold on
subplot(2,1,2)
bode(G)
title('PD调节后系统的波德图')

Published with MATLAB® R2016b