逻辑代数基础介绍——数电第二章学习

逻辑代数经常涉及到的电路

所有基础都是基于最基本的与、或、非电路

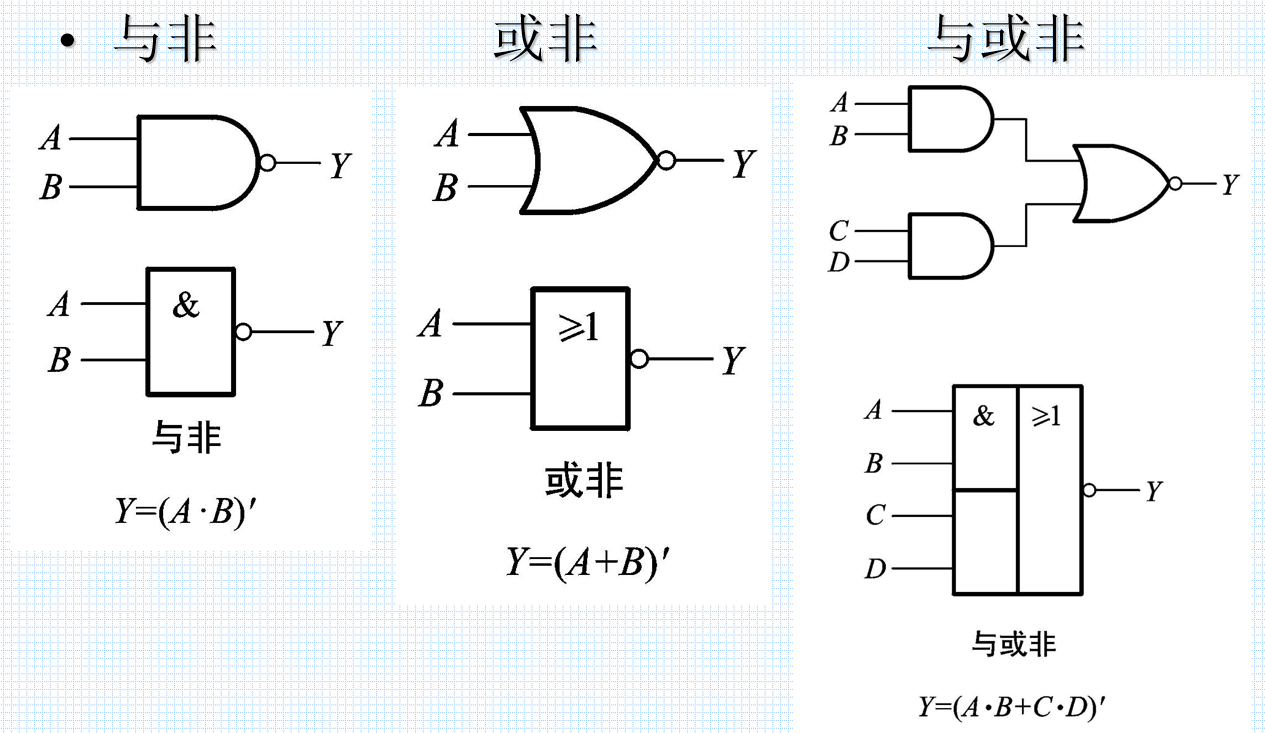
异或：相同则0，不同则1

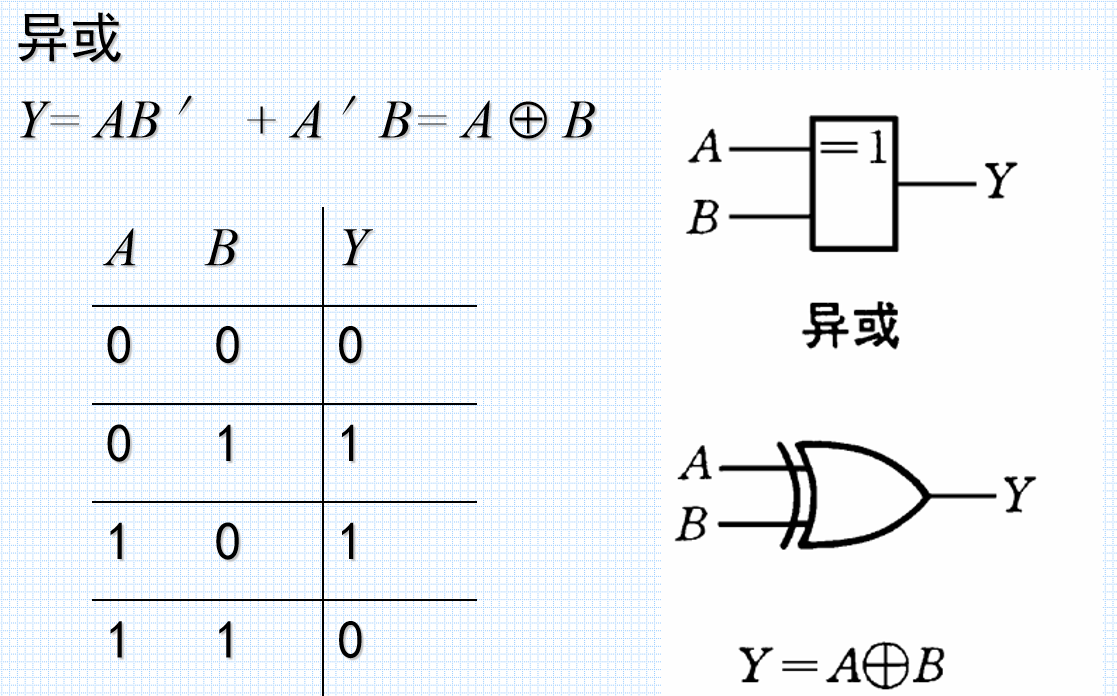
同或：相同则1，不同则0

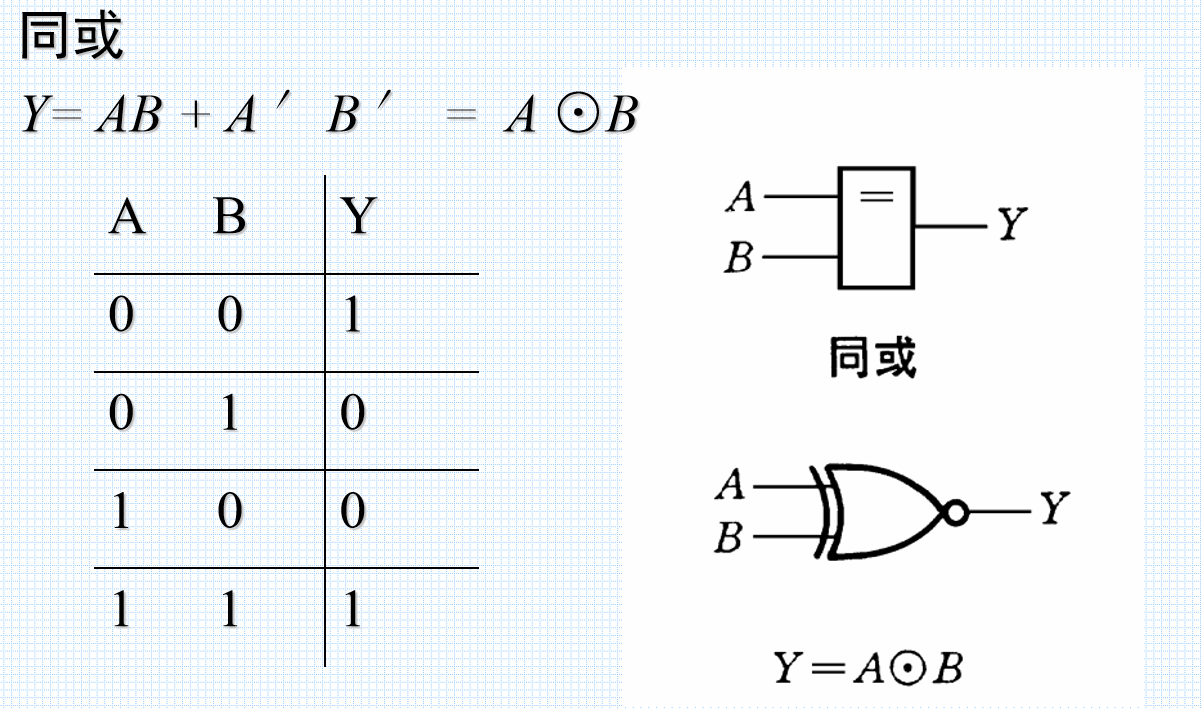
一些常见的逻辑运算

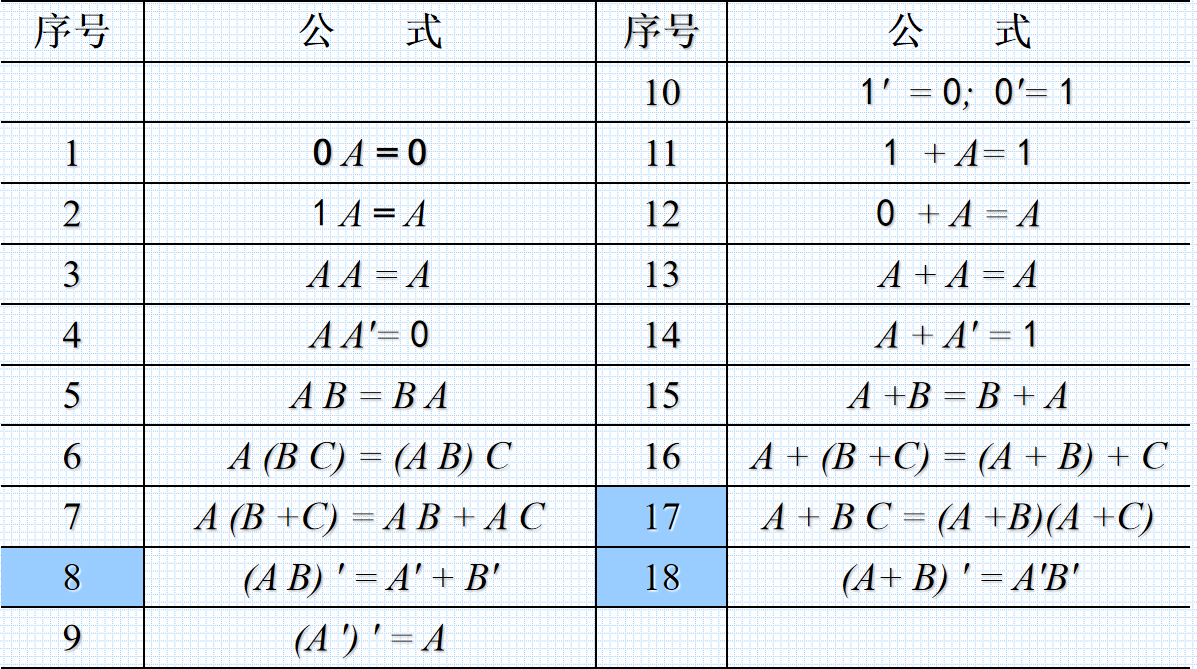
以及一些推导出来的逻辑常用公式：

以上公式可通过基本公式运算得到，这里不予证明。
在应用中，我们需要通过真值表写出函数表达式。
具体过程如下：
1.找出真值表中使 Y=1 的输入变量取值组合。
2.每组输入变量取值对应一个乘积项，其中取值为1的写原变量，取值为0 的写反变量。
3.将这些变量相加即得 Y。

最小项

因为逻辑函数有非常多的表现形式，为了统一一种标准，设立了“最小项之和”和“最大项之积”这两种形式。
最小项 m：
m是乘积项
包含n个因子
n个变量均以原变量和反变量的形式在m中出现一次
n变量的最小项有2^n个

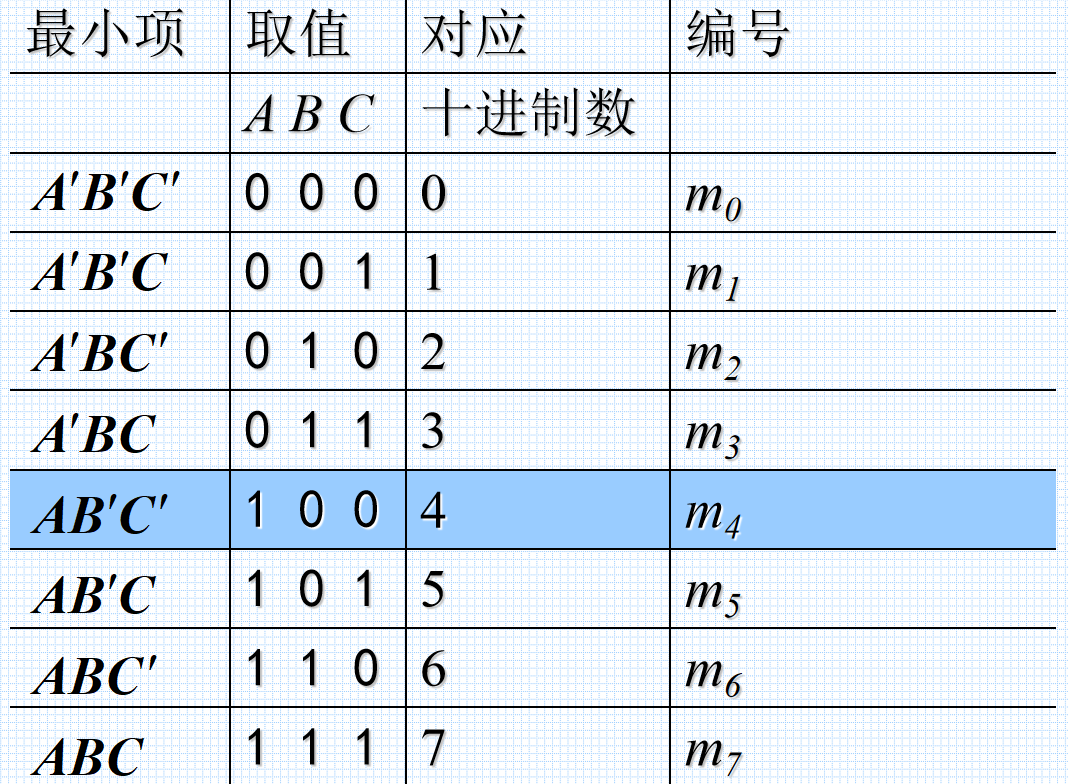
从上图可以发现，m的下标对应为ABC二进制数的十进制转换，如ABC为011时，m的下标为3。
（注：下面所说的最小项都是ABC的原变量或反变量形式）
1.在输入变量任一取值下，有且仅有一个最小项的值为1。
2.全体最小项之和为1 。
3.任何两个最小项之积为0 。
4.两个相邻的最小项之和可以合并，消去一对因子，只留下公共因子。
------相邻：仅一个变量不同的最小项,如：

A`BC`+ABC`=BC'

5.对于n变量函数，有2^n个最小项

常见化简成最小项之和的方法

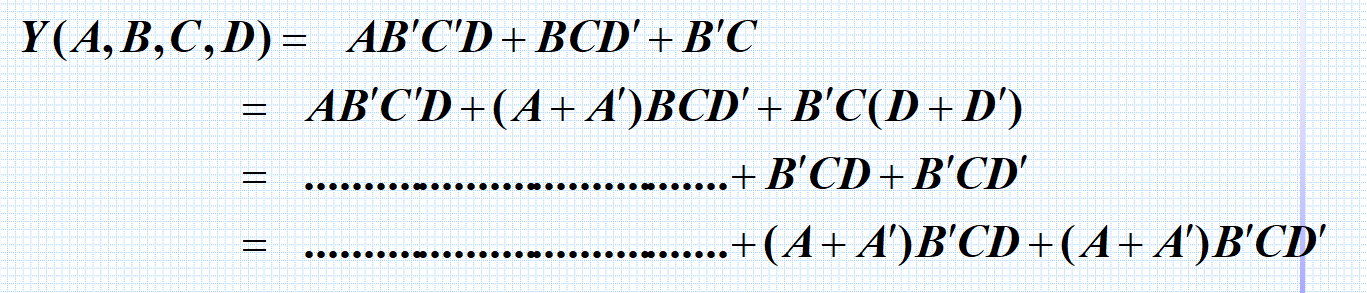
最大项

M是相加项；
包含n个因子。
n个变量均以原变量和反变量的形式在M中出现一次。

如：两变量A, B的最大项

A`+B`,A`+B,A+B.A+B`

1.在输入变量任一取值下，有且仅有一个最大项的值为0；
2.全体最大项之积为0；
3.任何两个最大项之和为1；
4.只有一个变量不同的最大项的乘积等于各相同变量之和。

最小项和最大项之间的关系：

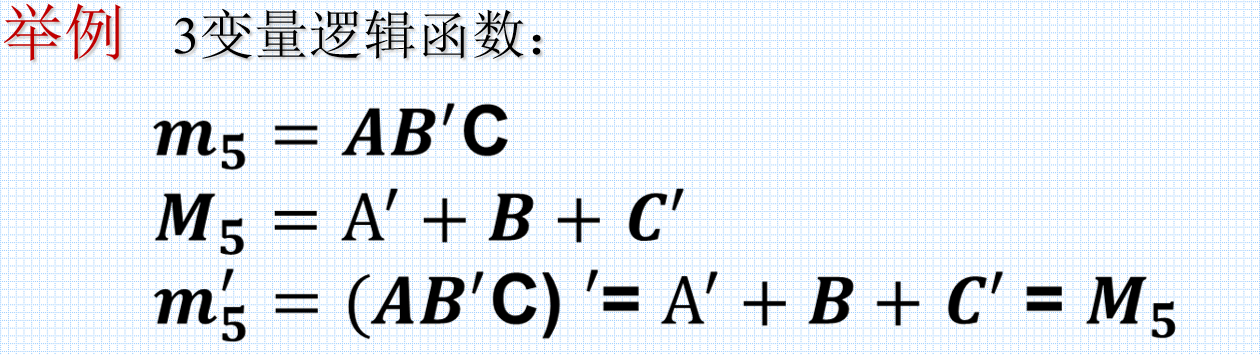
常见化简成最大项之积的方法

利用公式 A+BC = (A+B) (A+C)

Y=A`B+AC
=(A'B+A)(A`B+C)
=(A+B)(A`+C)(B+C)
=(A+B+CC`)(A`+C+BB')(B+C+AA`)
=(A+B+C)(A+B+C`)(A`+B+C)(A`+B`+C)

最后

以上就是勤劳小懒猪为你收集整理的逻辑代数基础介绍——数电第二章学习的全部内容，希望文章能够帮你解决逻辑代数基础介绍——数电第二章学习所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。