一 逻辑代数基本概念

1.基本逻辑运算

	逻辑表达式	运算逻辑符号	逻辑真值表
与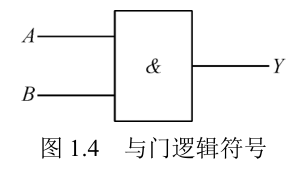
或	Y=A+B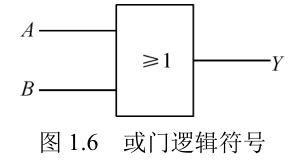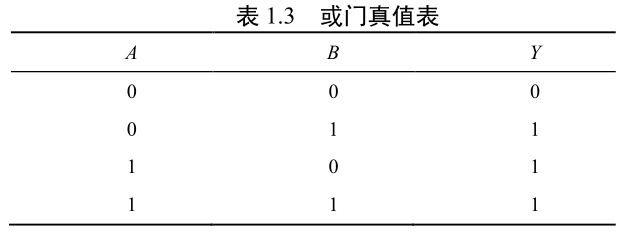
非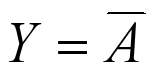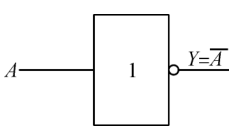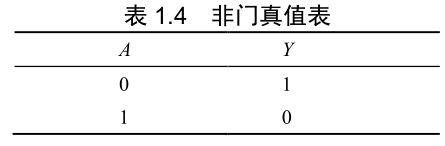
与非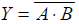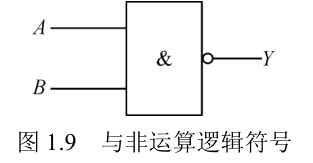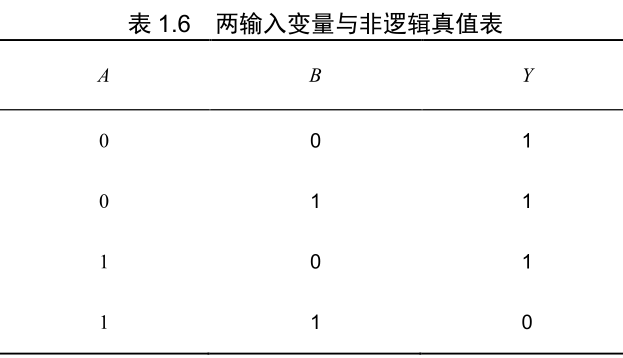
或非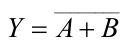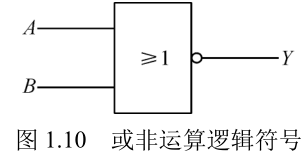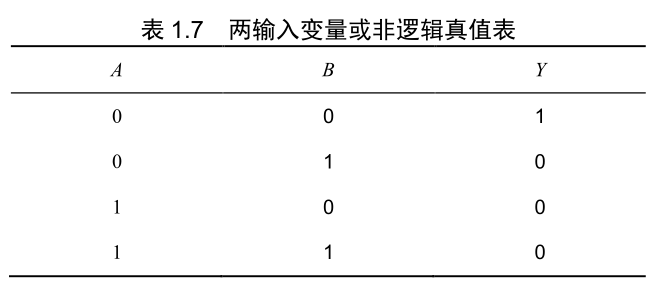
与或非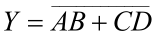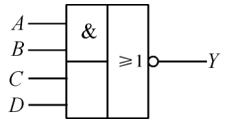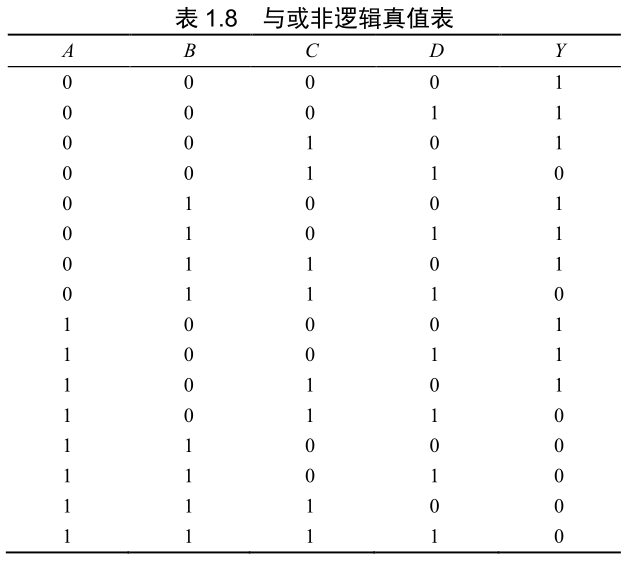
同或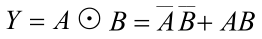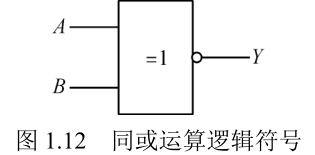
异或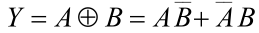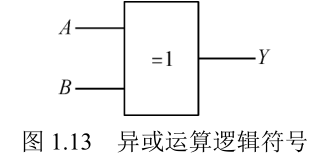

一些概念

• 与逻辑：在逻辑问题中，如果决定某一事件发生的多个条件必须同时具备，事件才能发生，则称这种因果关系为与逻辑，也可称为与关系、与运算
• 或逻辑：如果决定某一事件发生的多个条件中，只要有一个或一个以上条件成立，事件便可发生，则称这种因果关系为或逻辑，也可称为或关系（或运算）
• 非逻辑：如果某一事件的发生取决于条件的否定，即事件与事件发生的条件之间构成矛盾，则这种因果关系称为非逻辑，也可称为非关系、非运算。
• 与非逻辑：与逻辑运算和非逻辑运算的复合，它将输入变量先进行与运算，然后再进行非运算。在与非运算中，只要输入变量中有一个为 0，输出就为 1。只有输入变量全部为 1 时，输出才为 0。
• 或非逻辑：或非逻辑是或逻辑运算和非逻辑运算的复合，将输入变量先进行或运算，然后再进行非运算。在或非运算中，只要输入变量中有一个为 1，输出就为 0。或者说，只有输入变量全部为 0 时，输出才为 1。
• 与或非逻辑：与或非逻辑是与逻辑运算和或非逻辑运算的复合。它是先将输入变量 A、B 及 C、D 分别进行与运算，然后再进行或非运算。
• 同或逻辑：当两个输入变量 A 和 B 取值相同时，输出 Y 才为 1，否则 Y 为 0，这种逻辑关系称为同或运算
• 异或逻辑：当两个输入变量 A 和 B 取值不相同时，输出 Y 才为 1，否则 Y 为 0，这种逻辑关系称为异或运算
• 正负逻辑：正逻辑体制规定高电平为逻辑“1”，低电平为逻辑“0”；负逻辑体制规定低电平为逻辑“1”，高电平为逻辑“0”。数字电路的输入量和输出量一般用高、低电平表示。
• 逻辑变量：在逻辑代数中，使用英文字母来表示变量，并将其称为逻辑变量。
• 逻辑函数：在上述三个逻辑表达式中，式中的 A 、 B 称为输入逻辑变量，Y 为输出逻辑变量，字母上面无反号的称为原变量，有反号的称为反变量。三个表达式准确描述了与、或、非三种基本逻辑关系。

2.逻辑运算的基本定律

公式名	表达式
交换律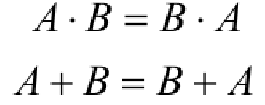
结合律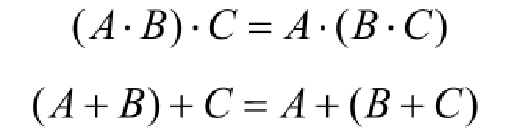
分配律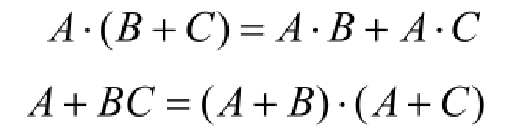
同一律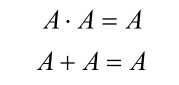
还原律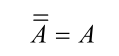
摩根定理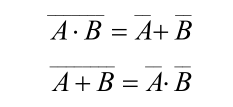

常量之间的关系

常量之间 与关系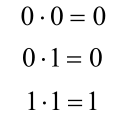
常量之间 或关系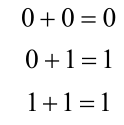
常量之间 非运算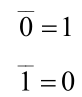

变量与常量的关系

与关系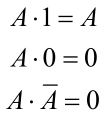
或关系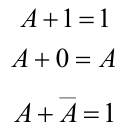

3.三个基本规则

(1)代入规则

(2)反演规则
已知函数 F，要求其反函数 时，只要将 中所有原变量变为反变量、反变量变为原变量、与运算变成或运算（乘变加）、或运算变成与运算（加变乘）、0 变为 1、1 变为 0、两个或两个以上变量公用的长“非”号保持不变，便得到 ，这就是反演规则。

(3)对偶规则
函数中各变量保持不变，而所有的与运算变为或运算（乘变加）、所有的或运算变为与运算（加变乘）、0 变为 1、1 变为 0、两个或两个以上变量所公用的长非号保持不变，则得到一个新函数 ， 就是 对偶函数，这就是对偶规则。

4.最小项表达式

5.最简表达式

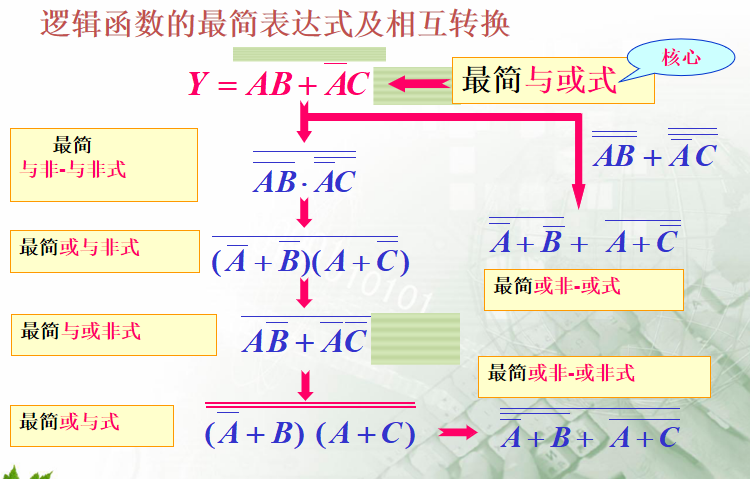
（1）最简与或式(重点/核心)：乘积项的个数最少，每个乘积项中相乘的变量个数也最少的与或表达式，叫做最简与或表达式

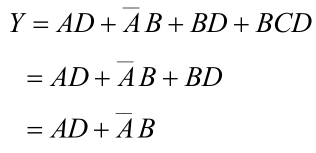
（2）最简与非-与非式：非号最少，每个非号下面相乘的变量个数也最少的与非-与非式，叫做最简与非-与非表达式。注意，单个变量上面的非号不计算在上述定义中，因为已将其当成反变量

（3）最简或与式：括号个数最少，每个括号中相加的变量的个数也最少的或与式，叫做最简或与表达式。在将函数的反函数化简为最简与或表达式的基础上，再一次取反，然后用摩根定理去掉反号，便可得到函数的最简或与表达式

(4)最简或非-或非式：非号个数最少，非号下面相加变量的个数也最少的或非-或非式，叫做最简或非-或非表达式。
解法：在最简或与式的基础上，两次取反，再用摩根定理去掉下面的反号，所得到的便是函数的最简或非-或非表达式。

(5)最简与或非式：在非号下面相加的乘积项的个数最少，每个乘积项中相乘的变量个数也最少的与或非式，叫做最简与或非表达式。

二 逻辑函数公式法化简

常用化简方法

并项法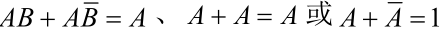
吸收法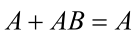
消去法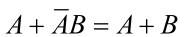
配项消项法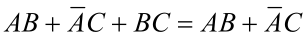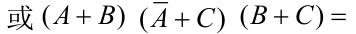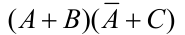

1.并项法

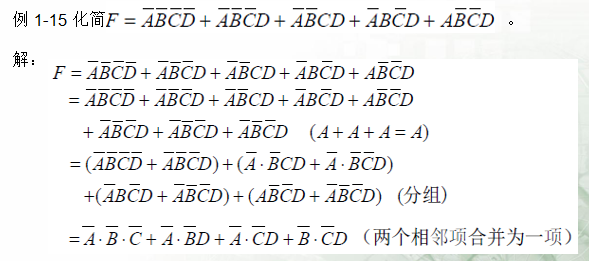
2.吸收法

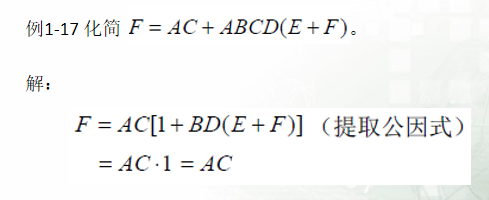
3.消去法

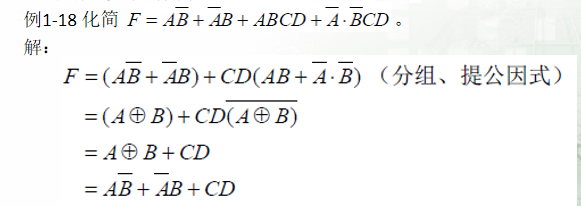
4.配项消项法

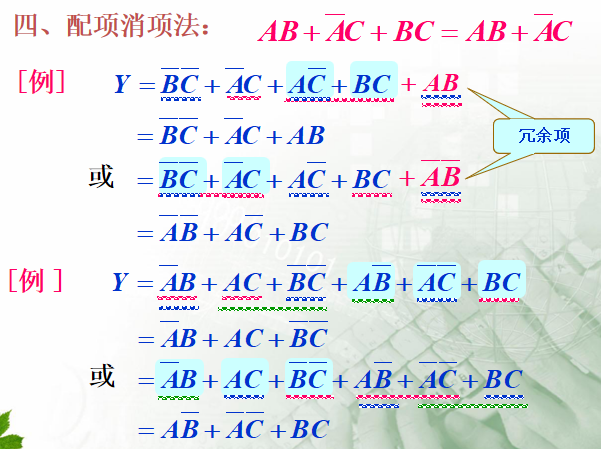
5.综合练习

三 逻辑函数卡诺图化简

卡诺图(Karnaugh maps)： 凡两个逻辑相邻项可合并成一项。按照这个规律，可以把逻辑函数中的各个最小项用图形表示出来，这种图就叫卡诺图。
卡诺图缺点： 函数的变量个数不宜超过 6 个
卡诺图特点： 用几何相邻表示逻辑相邻

逻辑相邻： 两个最小项只有一个变量不同

几何相邻

1. 相接：紧挨着
2. 相对：行或列的两头
3. 相重：对折起来位置重合

逻辑相邻的两个最小项可以合并成一项，并消去一个因子。如：

需要强调的是，为了符合相邻原则， 排列次序必须是“00、01、11、10”，这样排列就保证了 与它的三个相邻方格 在逻辑上是相邻的，即 与它的三个相邻最小项都仅有一个变量取值不同。

卡诺图的结构： 对于有 n 个变量的逻辑函数，全部最小项的个数有 2的n次方个，因而对应卡诺图中的小方格就有 2的n次方个

1.变量卡诺图的画法

两变量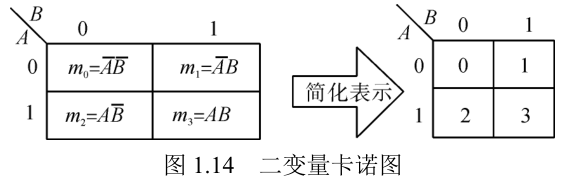
三变量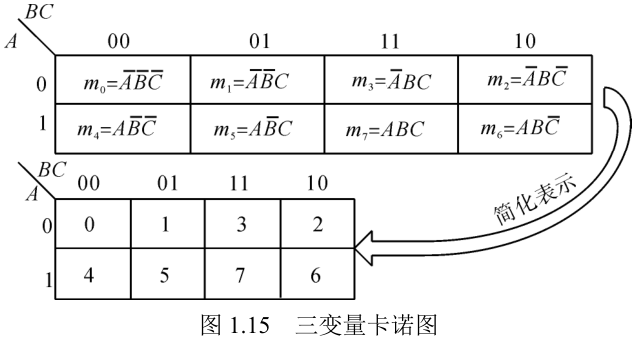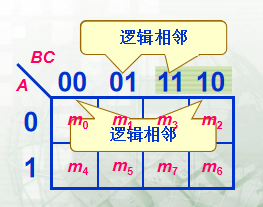
四变量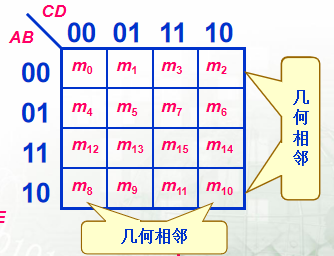
五变量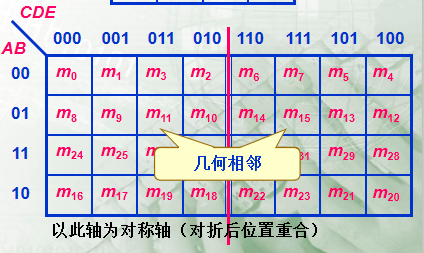

2.卡诺图最小项 合并规律

2的n次方 个相邻最小项合并可以消去 n 个因子

(1) 两个相邻最小项合并可以消去一个因子（消去那个不同的）

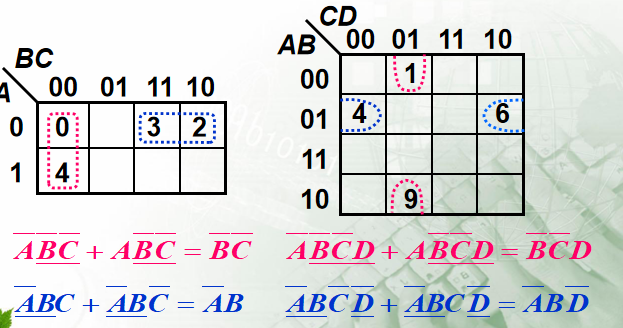
(2) 四个相邻最小项合并可以消去两个因子

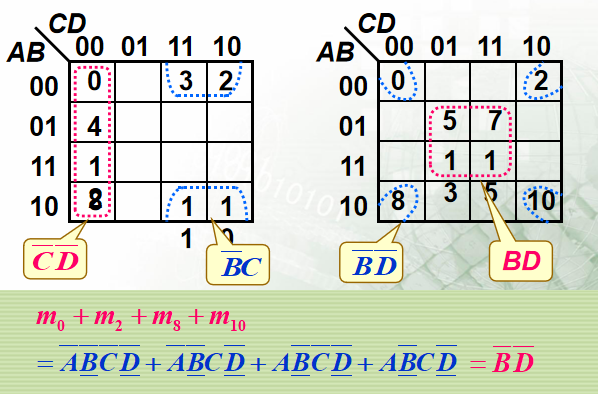
(3) 八个相邻最小项合并可以消去三个因子

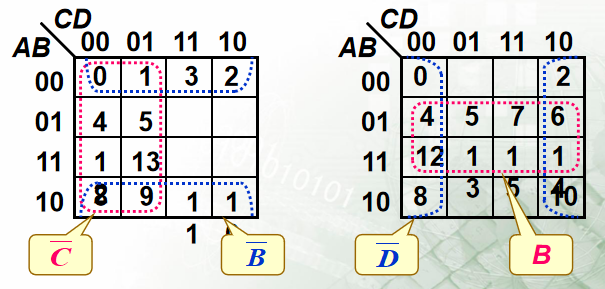
3.逻辑卡诺图化简

步骤

1. 根据最小项中的最大数确定变量的个数，然后画出相应的卡诺图
2. 画圈，方格数符合2的n次方关系，遵循的原则是： 圈越大越好，圈的总数越少越好，允许重叠。每个圈内至少有一个别的圈未包括进去的”1“。
3. 找相同，相与。得到最简表达式

口诀
天涯海角：B反D反
中心四子：BD

例子

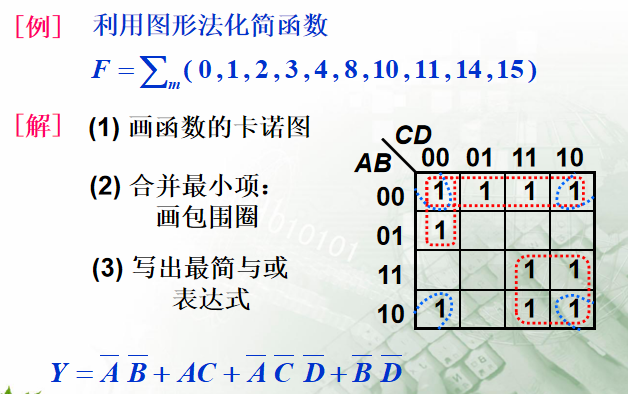
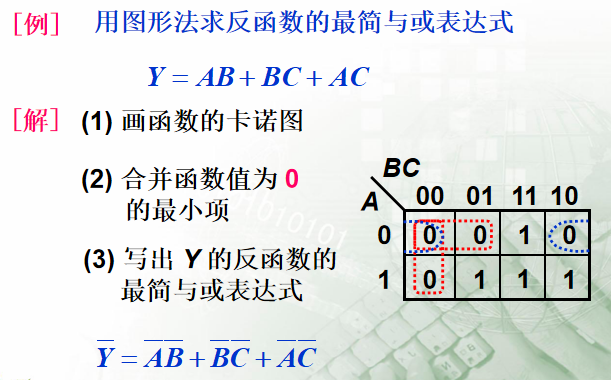
四 具有无关项的逻辑函数化简

完全定义函数： 任意逻辑函数，其函数值非“0”即“1”，即对于有 个变量的函数来说，其最小项共有 2N 个，若其中 个最小项使函数值为“1”，则其余 个最小项就使函数值为“0”，这样的函数称为完全定义函数

无关项： 函数取值无关的最小项称为无关项，有时也称为约束项、任意项、禁止项。（实际工程问题中，一个 变量的函数并不一定与 2的n次方个最小项都有关，而仅与其中一部分有关）

约束项： 不会出现的变量取值所对应的最小项。

约束条件： 由约束项相加所构成的值为 0 的
逻辑表达式。

约束条件的表达方式

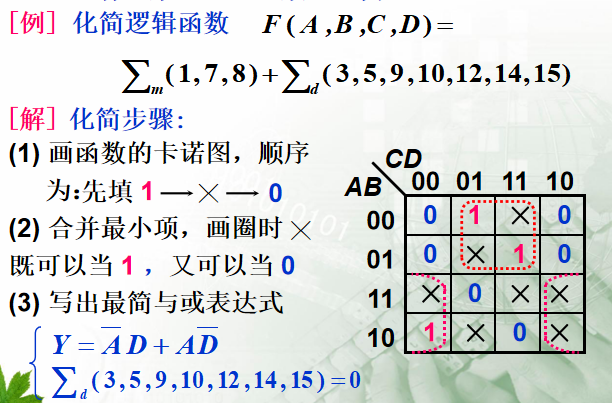
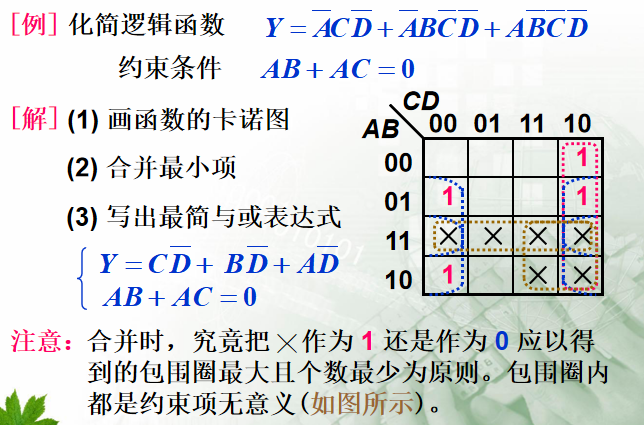
1. 在真值表和卡诺图上用叉号(╳)表示。x作为1/0以得到的包围圈最大且个数最少为原则
2. 在逻辑表达式中，用等于 0 的条件等式表示。

1. 具有约束的逻辑函数的化简

五 逻辑函数的表示方法及其相互之间的转换

方法	表现形式	优点	缺点
逻辑表达式	Y=AB+BC+CA	书写简洁方便，易用公式和定理进行运算、变换。	逻辑函数较复杂时，难以直接从变量取值看出函数的值。
真值表		直观明了，便于将实际逻辑问题抽象成数学表达式	难以用公式和定理进行运算和变换；变量较多时，列函数真值表较繁琐
卡诺图		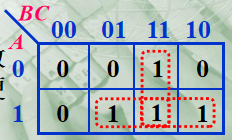便于求出逻辑函数的最简与或表达式	只适于表示和化简变量个数比较少的逻辑函数，也不便于进行运算和变换
逻辑图		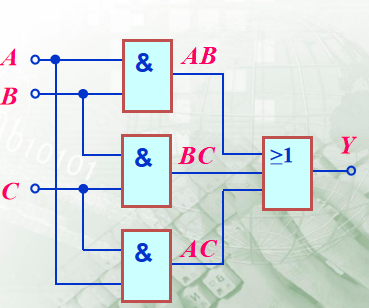最接近实际电路	不能进行运算和变换，所表示的逻辑关系不直观
波形图		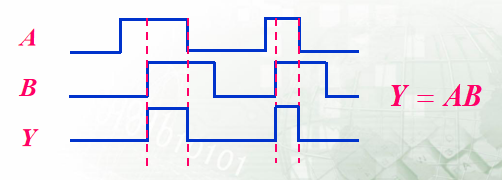形象直观地表示了变量取值与函数值在时间上的对应关系。	难以用公式和定理进行运算和变换，当变量个数增多时，画图较麻烦

最后

以上就是背后小鸽子为你收集整理的【数电】第一章 逻辑代数基础一 逻辑代数基本概念二 逻辑函数公式法化简三 逻辑函数卡诺图化简四 具有无关项的逻辑函数化简五 逻辑函数的表示方法及其相互之间的转换的全部内容，希望文章能够帮你解决【数电】第一章 逻辑代数基础一 逻辑代数基本概念二 逻辑函数公式法化简三 逻辑函数卡诺图化简四 具有无关项的逻辑函数化简五 逻辑函数的表示方法及其相互之间的转换所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。