数电(第二章、逻辑电路)

逻辑电路概述
~逻辑代数
~基本运算，公式和定理
~逻辑函数的表示，转换和化简
1). 数字电路分析与设计工具：逻辑代数

2). 逻辑：事物之间的因果关系。

3). 逻辑代数：逻辑运算的数学方法（布尔代数）

4). 数字中的逻辑代数：二值逻辑，逻辑变量的取值只有0和1两种情况；

5). 逻辑代数中的三种基本运算

	与 (AND)	或(OR)	非(NOT)	异或	同或
条件	条件同时具备，结果发生	条件有一个具备，结果发生	条件不具备，结果发生	取值不同时，发生	取值相同时，发生
符号表示	Y=A AND B=A&B=A*B=AB	Y=A OR B=A+B	Y=NOT A=A’	Y=A⊕B=AB’+A’B	Y=A⊙B =AB+A‘B’
国家标准符号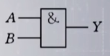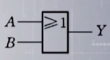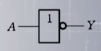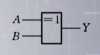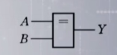
国际标准符号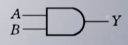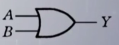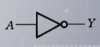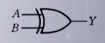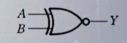

6). 几种常见的复合逻辑运算

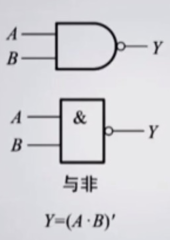
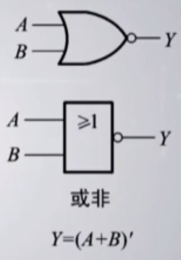
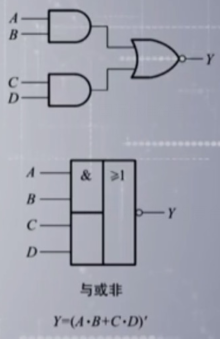
7). 基本公式

$证明：A+BC=(A+B)(A+C)$
$证：右=AA+AC+BA+BC=A(1+B+C)+BC=A+BC=左$

8). 常用公式
$1.A+AB=A$
$2.A(B+C)=A$
$3.AB+A{B}^{\prime }=A$
$4.A+A^{\prime }B=A+B$
$5.AB+A^{\prime }C+BC=AB+A^{\prime }C;AB+A^{\prime }C+BCD=AB+A^{\prime }C$
$6.A(AB{)}^{\prime }=A{B}^{\prime };A^{\prime }(AB{)}^{\prime }=A^{\prime }$

逻辑电路中的基本定理
1). 代入定理
在任何一个包含A的逻辑等式中，若以另外一个逻辑式代入式中A的位置，则等式依然成立。
$例：1.A+BC=(A+B)(A+C)$
$A+B(CD)=(A+B)(A+CD)=(A+B)(A+C)(A+D)$
$例：2.(AB{)}^{\prime }=A^{\prime }+B^{\prime }$
$(ABC{)}^{\prime }=A^{\prime }+B^{\prime }+C^{\prime }$

2). 反演定理
对任意逻辑式$Y=>Y^{\prime }$，即对于任意一个逻辑式Y，若将其中所有的“与”换成“或”，“或”换成“与”，0换成1，1换成0，原变量变成反变量，反变量变成原变量，则得到一个新的逻辑式即为逻辑式Y的非，这个规律称为反演定理。
$\ast =>+,$ $+=>\ast ,$ $0=>1,$ $1=>0$
$例：Y=A^{\prime }(B+C)+CD$
$Y^{\prime }=(A+B^{\prime }{C}^{\prime })(C^{\prime }+D^{\prime })=A{C}^{\prime }+B^{\prime }{C}^{\prime }+A{D}^{\prime }+B^{\prime }{C}^{\prime }{D}^{\prime }(B^{\prime }{C}^{\prime }{D}^{\prime }可省略)$
$注：反演定理按优先级高低进行取反。$
3). 对偶定理
对偶式指的是对于任何一个逻辑式Y，若将其中的“·”换成“+”，“+”换成“·”，0换成1，1换成0，则得到一个新的逻辑式Y’，Y’就是Y的对偶式。显然Y和Y’互为对偶式。

4). 逻辑函数的表示方法
~真值表
~逻辑式
~逻辑图
~波形图

5). 真值表转逻辑式
1.找出真值表中使Y=1的输入变量取值组合。
2.将每个取值给写成一个与项，其中取值为1的用原变量，取值为0的用反变量。
3.将这些与项相或即得Y。
最小项
1). n变量逻辑函数的m
~m是与项
~包含n个因子
~n个变量均为原变量或反变量的形式在m中出现一次。对n变量的逻辑函数，有$2^n$个最小项
例如：两变量A，B的最小项
A’B’,A’B,AB’,AB($2^2=4$个)
最小项编号：以其二进制所对应的十进制进行编号。例：A’B:为01，那么对应$m_1$
最小项性质：
$\cdot$在输入变量任意取值的情况下，有且仅有一个最小项的值为1
$\cdot$全体最小项之和为1
$\cdot$任何两个最小项之积为0
$\cdot$两个相邻的最小项之和可以合并，消去一个共同因子，只留公共因子。
$相邻:$仅一个因子不同的自小项。如：A’BC与A’BC’，A’BC+A’BC=A’B。
列：Y(A,B,C)=ABC’+BC=ABC’+BC(A+A’)=ABC’+ABC+A’BC=$\sum m(3,6,7)$
最小项的逻辑形式一定是唯一的。

最大项
1). n变量逻辑函数的M
~M是或项
~包含n个因子
~n个变量均为原变量或反变量的形式在M中出现一次。对n变量的逻辑函数，有$2^n$个最大项
例如：两变量A，B的最大项
A’+B’,A’+B,A+B’,A+B($2^2=4$个)
最大项编号：以其二进制所对应的十进制进行编号。例：A’+B:为10，那么对应$m_2$
最大项性质：
$\cdot$在输入变量任意取值的情况下，有且仅有一个最大项的值为0
$\cdot$全体最大项之积为0
$\cdot$两个相邻的最大项之积可以合并，消去一个共同因子，只留公共因子。
$相邻:$仅一个因子不同的自小项。如：A’+B+C和A’+B+C’，(A’+B+C)(A’+B+C)=A’+B。
列：Y(A,B,C)=(A+B+C’)(B+C)=(A+B+C’)(B+C+AA’)=(A+B+C’)(A+B+C)(A’+B+C)=$\prod M(3,6,7)$
最大项的逻辑形式一定是唯一的。

卡诺图
$\cdot$ 逻辑函数最小项之和的一种图形表示。
$\cdot$用$2^n$个小方格分别代表n变量的所有最小项，并将它们排列成矩阵，而且使几何位置相邻的两个最小项在逻辑上也是相邻的——就得到卡诺图。
~卡诺图的表示方法:

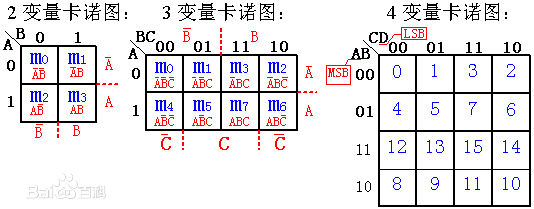
1). 用卡诺图表示逻辑函数
$\cdot$将逻辑函数表示为最小项之和的形式
$\cdot$在卡诺图上与这些最小项对应的方格上填入1，其余方格填入0。
简化方案：
确定使每个与项为1的所有输入变量取值，并在卡诺图上对应方格填入1。其余补0。
2). 逻辑函数的卡诺图化简法
$2^n$个相邻最小项，可合并为一项，消去n个因子。
化简原则：
$\cdot$与项的数目最少，即圈成的矩形数量最少；
$\cdot$每个与项的因子最少，即圈成的矩形最大；
$\cdot$保证每个圈至少有一个"1"只被圈过一次，否则该圈是多余的。
3). 具有无关项的逻辑函数的化简
1.约束项：逻辑函数中输入变量取值有限制，与这些被限制的取值对应的最小项称为约束项。
2.任意项：在输入变量某些取值下，函数值为1或0，不影响逻辑电路的功能，这些取值对应的最小项称为任意项。
无关项：约束项和任意项统称为无关项，可写入逻辑式，也可不写入逻辑式。
$$F=\sum m+\sum d$$

最后

以上就是专一电灯胆为你收集整理的数电(第二章、逻辑电路)的全部内容，希望文章能够帮你解决数电(第二章、逻辑电路)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。