matlab 脉冲密度调制,基于脉冲密度调制技术的AGC性能的电路设计

自动增益控制电路在通信系统领域有着非常广泛的应用，主要用于各种接收芯片的中频级和射频级，实现压缩动态范围，抑制干扰脉冲和抗快衰落等作用。然而传统的基于脉冲宽度调制波形输出的AGC电路在环路稳定性上较差，收敛速度慢，外围所需的元器件也较多，因而体积较大，这些极大地制约了AGC电路的性能。因此尝试采用基于脉冲密度调制技术的AGC电路，以克服基于PWM技术的AGC电路的种种性能瓶颈。

1、AGC电路概述

在各种通信系统中，受发射功率大小，收发距离远近，信号在传输媒介中会出现明显的衰落等因素的影响，作用在接收机输入端的信号强度有很大的变化和起伏。然而信道解调部分只能处理幅度变化不大的信号，信号过强、过弱或忽大忽小，都会使解调失败。所以必须要有一个AGc电路，使接收机的输入端能处理幅度变化很大的信号，而解调部分能收到一个平稳适中的信号，以进行信道解调。AGC电路可以使振幅变化范围非常大的输入信号，输出时振幅变化范围非常小，从而保证输入到ADC的信号位于ADC最佳的工作范围，AGC电路的功能框图如图1所示。

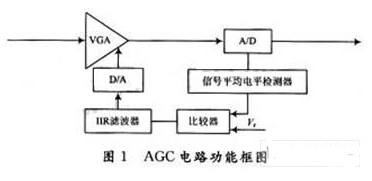
图1中的A／D转换器将输入进来的模拟信号采样量化为数字量后，经过信号平均电平检测器算出平均电平，该平均电平与预先设定的参考电平值V，相比较，得到平均电平误差，将该误差送入IIR滤波器进行平滑累加后得到与所期望的AGC增益相对应的数字量(AGC控制字)，最后通过D／A转换器送入可变增益放大器(VGA)。

在上述这些模块中，D／A模块有多种方案可选。由于该模块涉及到制造工艺和系统的外围电路，而且D／A转换器必须占用一定空间及消耗一定量的功率，因此D／A转换器方案的选取，将对AGC甚至整个系统的性能和成本产生很大的影响。

D／A转换器一般有下面三种方案可选：

(1)直接使用专用的D／A转换芯片。这种方案转换速度快，但成本太高，一般不予采用。

(2)脉冲宽度调制器(PWM)+RC滤波器的方案。该方案成本低廉，但是D／A转换速度慢，AGC电路达到收敛的时间长，严重时会产生振荡。该方案在对AGC环路稳定性和收敛速度要求不高的通信系统中经常被使用。

(3)脉冲密度调制(PDM)+RC滤波器的方案。该方案可以克服PWM波的诸多缺点，但成本较高，适用于对控制要求较高的系统。

2、PDM与PWM的原理及比较

2.1PWM理论及其特点

PWM是一种通过改变高低电平的比值来得到不同输出电压的调制方式。该调制输出周期为T，占空比为N／M(N，M必须是整数)的方波。

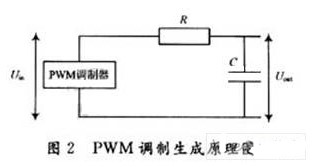
如图2所示，电容C上的电压就是PWM的输出电压Uout，在RC值足够大时，Uout=Uin·(N／M)。PWM的精度与M有着很大的关系。当M=2时，只有0，1／2和2／2三种电压输出；而到M=256时，就有0，1／256，2／256，3／256，…，256／256一共257种电压输出。M的大小取决于VGA的精度。一般来说，VGA能达到10位以上的精度，就是说M的取值要在1024以上。随着M的增大，RC的值也将相应增加，否则Uout就会呈现出明显的锯齿状波形，使增益波动，恶化解调性能。但是如果让RC增大，在增加元器件成本的同时，还会使Uout对IIR滤波器产生的数字量变化响应变慢，延长AGC收敛时间，甚至造成AGC的振荡，这在AGC电路的设计中是严格禁止的。

2.2PDM原理

PWM的周期T是固定的，改变的是高低电平的占空比；而PDM的脉冲宽度(高电平宽度)是固定的，改变的是脉冲的密集程度，脉冲密集，Uout就越高；脉冲稀疏，则Uout就越低。图3给出电压为5／16时的PDM与PWM波形。

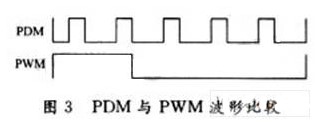
可见，PDM相当于在时域上被打散的PWM。由于PDM的高低电平分布较为均匀，因此在R，C值较小的系统里，也可以滤除高频交流分量，从而克服PWM的缺点。

2.3PDM的实现

假设PDM的脉冲周期为△T，将时钟信号送入N位计数器，实现0，1，…，2N-1的计数。在计数的单个脉冲周期△T里，将计数结果各个位上的逻辑值经过一系列逻辑操作，实现N位比较基准脉冲信号，分别为B0，B1，B2，…，B(N-1)。在每一个△T里，都只有一个位上有逻辑“1”，其他位上均为逻辑“0”。同时将输出的N位数据与该比较基准脉冲信号B0，B1，B2，…，B(N-1)进行逐位与操作，再将各个位上的结果相或，便得到△T内的调制结果。

对于N位的信号，周期为T=2N×△T。对于8位数字信号，PDM调制结果为：

PDMout=B7&D7+B6&D6+B5&D5+B4&D4+B3＆D3+B2＆D2+B1＆D1+B0&D0

其中，B0～B7为比较基准脉冲信号的低位到高位，而D0～D7为数字信号的低位到高位。

如图4所示，就是8位的PDM比较基准脉冲信号。其中，B7～B0的波形分别对应10000000B，01000000B，00100000B，…，00000001B的PDM调制方波。

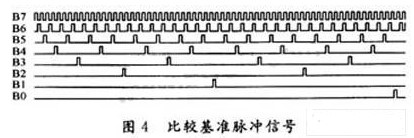
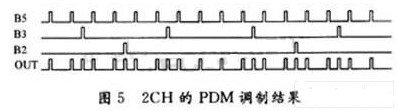
例如，对十六进制数2CH进行PDM调制。2CH对应的二进制数为“00101100”。其中，B5，B3，B2为“1”，其他各位均为“0”，经过逐位逻辑操作得：

PDMout=B7&0+B6&0+B5&1+B4&0+B3&1+B2＆1+B1&0+B0＆0=B5+B3+B2

经过一个周期的调制，使得到图5所示的PDM调制信号。这样8位的数字信号就转化为1位的脉冲信号。

在实际工程应用中，通常在系统中使用一个∑-△调制器来产生PDM波形。∑-△调制器的结构如图6所示。

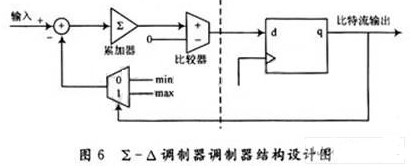
寄存器输出的比特流中高电平的密度代表了输入信号的幅度。如果图6中虚线左侧部分是模拟电路，输入的是模拟信号，那么单位时间内输出比特流中1的个数就反映了输入模拟信号的幅度，实现A／D转换功能。如果虚线左侧部分是数字电路，输人的是若干比特宽的数字量，那么对输出的比特流进行低通滤波后，就得到了相应的电压，实现的是D／A转换功能。本AGC电路中使用的是∑-△调制器的D／A功能，并且输入范围为0～1023，可实现足够精确的D／A转换。

3、PDM与PWM的仿真比较

3.1PDM与PWM收敛时间仿真比较

图7是用Matlab对PDM和PWM进行的仿真对比。其中，电路参数：VGA增益为15dB／V，R=100Ω，C=0.1μF，AGC工作时钟为10MHz。

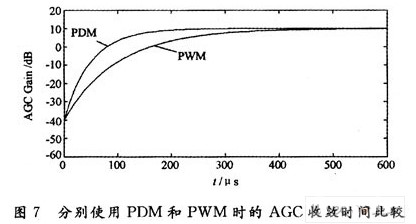
从图7中可以看出，在相同的R，C条件下，使用PDM调制的AGC电路，在收敛时间上小于使用PWM调制的AGC电路。

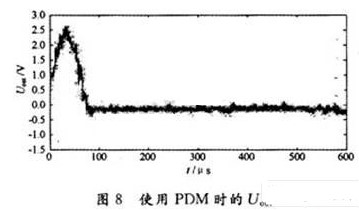
3.2PDM与PWM环路稳定性仿真比较

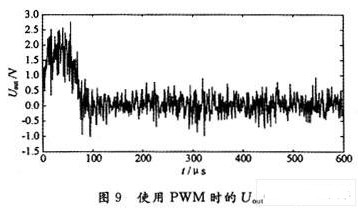
从图8和图9中可以看出，在相同的R，C条件下，使用PDM调制的AGC电路，Uout的抖动小于使用PWM调制的AGC电路，环路稳定性明显较好。

4、结语

本文通过PDM和传统的PWM两种调制方式的比较，最终得出使用PDM调制方式来充当AGC电路的D／A转换器，从而控制前端VGA的增益的方案。该方案相对于PWM方案具有更短的AGC收敛时间和更稳定的环路特性。通过Matlab仿真验证，表明了该方案的可行性。