系统定义及转换

(1)连续系统的传递函数模型

sys=tf(num,den)
%tf()代表采用传递函数形式建立系统模型
%num和den表示分子和分母系数构成的两个向量，当传递函数复杂时，应用多项式乘法函数conv()等实现

sys=tf(num,den，‘inputdelay’，tao)
%建立的是带时间延迟的系统传递函数

［num,den]=tfdata(sys,’v’)
%函数tfdata()，可从传递函数模型中提取模型中的分子分母多项式系数
%v为关键词，其功能是返回行向量(row vector)形式的分子分母多项式系数

(2) 零极点增益模型

%在MATLAB中零极点增益模型用[z,p,K]矢量组表示。即：
z=[z1,z2,…,zm]
p=[p1,p2,...,pn]
K=[k]
%K为系统增益，z为零点，p为极点

%建立零极点形式数学模型的函数zpk()
sys=zpk(z,p,k)
sys=zpk(z,p,k,’inputdelay’,tao)
%前者建立常规系统零极点形式的数学模型，后者建立的是有时间延迟系统的零极点形式数学模型。

%提取模型中零极点和增益的函数zpkdata()
%zpkdata()，可从零极点模型中提取模型中的零极点和增益，格式为：
［z,p,k]=zpkdata(sys,’v’)
%v为关键词，其功能是返回列向量（colum vector）形式的分子分母多项式系数。

系统联结

(1) 并联：parallel

%功能：并联连接两个系统。
%说明：parallel函数按并联方式连接两个系统，它既适合于连续时间系统，也适合于离散时间系统。
SYS = parallel(SYS1,SYS2)
SYS = SYS1+SYS2

(2）串联：series

%说明：series函数按串联方式连接两个系统，它既适合于连续时间系统，也适合于离散时间系统。
SYS = series(SYS1,SYS2)
SYS = SYS1*SYS2

(3) 反馈：feedback

SYS = feedback (SYS1,SYS2)
%将两个系统按反馈方式连接，如图。一般而言，统1为对象，系统2为反馈控制器。 feedback函数既适合于连续系统，也适合于离散系统。

零极点等 参量

pole

pole(SYS)
%计算线性系统的极点P = pole（SYS）返回动态系统SYS的极点P作为列向量。

pzmap

pzmap(SYS)
%pzmap（SYS）计算极点并动态系统的（传输）零SYS并将其绘制在复杂平面上。
%极点绘制为x和零以o表示。

tzero

z = tzero(sys)
%z = tzero（sys）返回多输入多输出（MIMO）动态系统sys的不变零。 如果sys是最小实现，则不变零与sys的传输零重合。

dcgain

dcgain(sys)
%k = dcgain（sys）计算LTI模型sys的DC增益k。

有理式分解及转换

%传递函数模型部分分式展开函数residue
[r,p,k]=residue(num,den)
%部分分式展开后，余数返回到向量r，极点返回到列向量p，常数项返回到k。
%将部分分式转化为多项式比p(s)/q(s)。
%当包含m重极点时，部分分式展开式将包括m项

［num，den］＝residue（r,p,k）
%可以将部分分式展开式返回到传递函数多项式之比的形式

系统的瞬态响应

LTI模型的阶跃响应

%STEP（SYS）绘制LTI的阶跃响应SYS模型（使用TF，ZPK或SS）。
%STEP（SYS，TFINAL）模拟步骤从t = 0到最终时间的响应t ＝ TFINAL。
%STEP（SYS1，SYS2，...，T）绘制步骤多种LTI模型的响应SYS1，SYS2，...在单个绘图上。 时间向量T是可选的。 您还可以指定一个每个系统的颜色，线条样式和标记，就像（sys1，'r'，sys2，'y-'，sys3，'gx'）一样。
%[Y，T] = STEP（SYS）返回输出响应Y和用于的时间向量T模拟。 屏幕上未绘制任何图。如果SYS具有NY输出和NU输入以及LT= length（T），Y是大小[LT NY NU]的数组其中Y（：，：，j）给出了阶跃响应第j个输入通道。
%[Y，T，X] = STEP（SYS）对于状态空间模型IS还返回状态轨迹X，如果SYS具有NX状态，则按LT-NX-NX-NU数组。

LTI模型的脉冲响应。

%IMPULSE（SYS）绘制的脉冲响应LTI模型SYS（使用TF创建，ZPK或SS）。
%IMPULSE（SYS1，SYS2，...，T）绘制步骤多个LTI模型SYS1，SYS2，...的响应在一个情节上。
%当使用左手参数调用时，[Y，T] = IMPULSE（SYS）返回输出响应Y和用于的时间向量T模拟。 屏幕上未绘制任何图。

LTI模型的时间响应任意输入

%LSIM（SYS，U，T）绘制了时间响应LTI模型SYS对输入信号的描述由U和T组成。时间向量T由规则间隔的时间样本，U是一个列与输入一样多的矩阵并且其第i行指定输入值在时间T（i）。
%LSIM（SYS1，SYS2，...，U，T，X0）模拟多个LTI模型SYS1，SYS2，...的响应在一个情节上。 初始条件X0为可选的。 您还可以指定颜色，线条样式和每个系统的标记，如lsim（sys1，'r'，sys2，'y-'，sys3，'gx'，u，t）。

算例

%任意输入的响应 lsim()
t=0:99;
p=rand(100,1)'
a=[1 2];
b=[1 2 3];
s1=tf(a,b);
step(s1)
impulse(s1)
lsim(s1,p,t)

t=0:0.01:5;
u=sin(t);
a=[1 2];
b=[1 2 3];
sys=tf(a,b);
lsim(sys,u,t)

评估系统的频率特性

连续系统的Nyquist图

%应用nyquist()函数:nyquist(sys)
%SYS可以是任一种类型的传递函数
k=100;
z=[-5];
p=[2 -8 -20];
GH=zpk(z,p,k);
nyquist(GH)

连续系统的Bode图

%应用bode()函数:bode(sys)
k=100;
z=[-5];
p=[2 -8 -20];
GH=zpk(z,p,k);
bode(GH)
[a,fai]=bode(sys,10)

%例题
%G(s)=7/3s+2 输入：1/7sin(2/3t+45) 稳态输出：Asin(2/3t+B)
q=tf(7,[3 2]);
[a1,a2]=bode(q,2/3);
A=a1*(1/7)
B=45+a2

%例题
%某系统传递函数为20/3s+10,当输入为3sin(4t+30°)+4cos(2t/3+45°)时，求系统稳态输出。
syms y1 y2 t;
q=tf(20,[3 10]);
[a1,a2]=bode(q,4);
[a3,a4]=bode(q,2/3);
A1=a1*3;
B1=30+a2;
A2=a3*4;
B2=45+a4;
y1=A1*sin(4*t+B1);
y2=A2*cos(2*t/3+B2);
y=y1+y2

LTI Viewer

LTI Viewer是图形用户查看和操作界面LTI模型的响应图。
您可以显示以下LTI的图类型使用LTI Viewer的模型：
•阶跃响应（仅适用于TF，SS或ZPK型号）
•脉冲响应（仅适用于TF，SS或ZPK
楷模）
•波德图
•奈奎斯特图
•尼科尔斯图
•频率响应的奇异值
•零点（仅适用于TF，SS或ZPK型号）
•LTI模型对一般输入的响应（仅适用于
TF，SS或ZPK型号）
•初始状态LTI响应（仅适用于SS型号）

判断系统稳定性

控制系统稳定的充分必要条件是：
1.系统特征方程式的根全部具有负实部。
2.闭环传递函数的极点全部具有负实部（位于左半s平面）。
显然，稳定性与零点无关。

系统稳定的判别方法：
1)特征方程－＞根的分布；
2)开环传递函数->闭环系统的稳定性；

%应用MATLAB判断系统稳定性
roots(den)；
pzmap(sys)；
pole(sys)

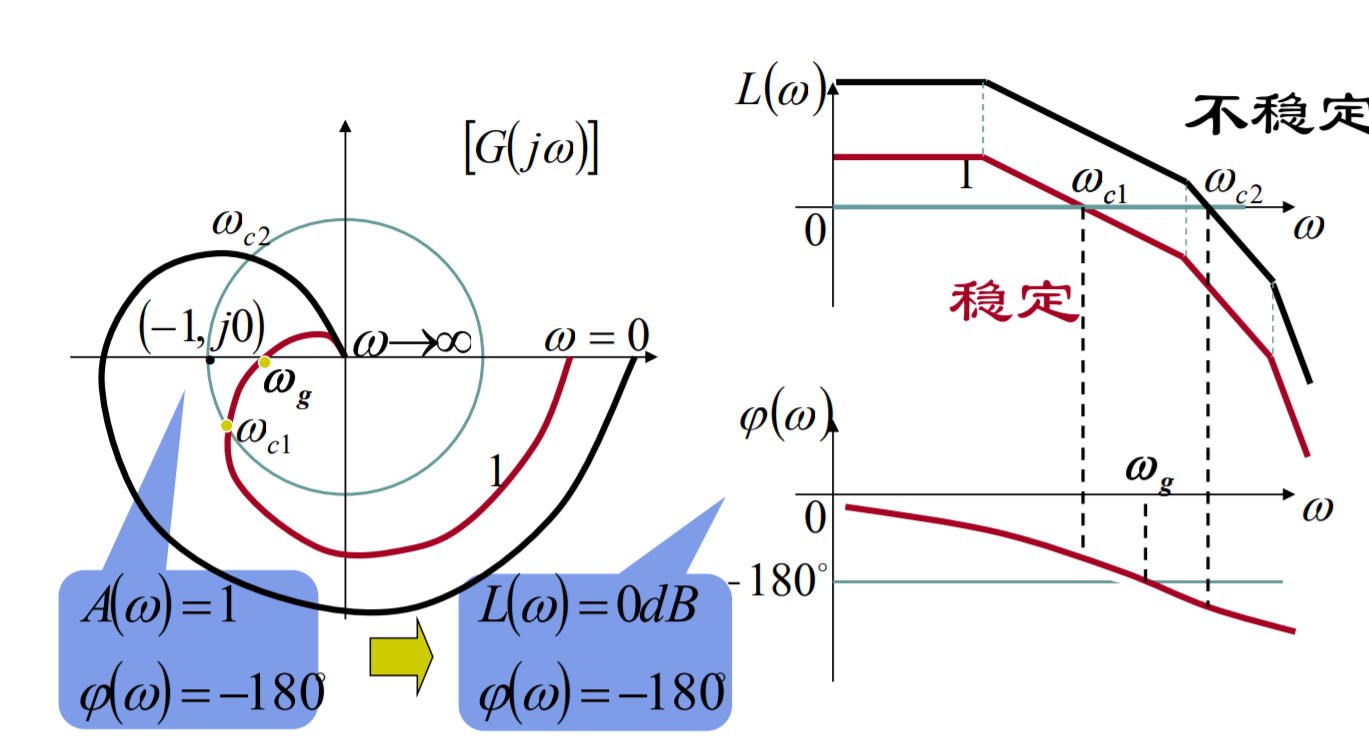
Nyquist图判断稳定性
一个闭环反馈控制系统稳定的充要条件：其开环乃氏图逆时针包围（-1，j0）点的圈数等于其开右极点的个数。

Bode图判断稳定性
若开环右极点个数为0 ，且在L（w）>=0 的所有w值上，ψ（w）>-180°，则闭环稳定

计算系统的相位裕量和幅值裕量

num=5*[0.0167 1];
den=conv(conv([1,0],[0.03,1]),conv([0.0025,1],[0.001,1]));
G=tf(num,den);
w=logspace(0,4,50);
bode(G,w);
[Gm,Pm,Wgm,Wpm]=margin(G) %该MATLAB函数在屏幕上绘制sys的Bode响应并指示图上相位裕量和幅值裕量
%Gm增益裕度和Pm相位裕度，Wpm测量相位裕量的频率和Wgm测量增益裕量的频率。

最后

以上就是炙热灰狼为你收集整理的Matlab （控制工程基础）学习笔记系统定义及转换系统联结零极点等 参量有理式分解及转换系统的瞬态响应评估系统的频率特性判断系统稳定性的全部内容，希望文章能够帮你解决Matlab （控制工程基础）学习笔记系统定义及转换系统联结零极点等 参量有理式分解及转换系统的瞬态响应评估系统的频率特性判断系统稳定性所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。