仿真图:
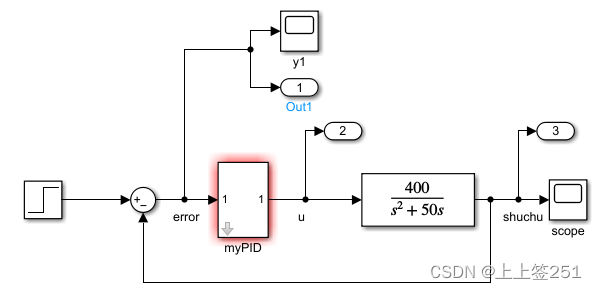
仿真主程序:
%遗传算法优化simulink仿真模型中的参数Kp Ki Kd
clear all;
close all;
Size=30;%种群中个体数,对应要优化的参数现有Size组(在后面会随机生成)
CodeL=3;%每个个体由codeL个元素,对应要优化的参数个数,对应要优化的参数Kp Ki Kd有3个
MinX(1)=zeros(1);
MaxX(1)=20.0*ones(1);
MinX(2)=zeros(1);
MaxX(2)=1.0*ones(1);
MinX(3)=zeros(1);
MaxX(3)=1.0*ones(1);%确定各优化参数的取值范围
E(:,1)=MinX(1)+(MaxX(1)-MinX(1))*rand(Size,1);
E(:,2)=MinX(2)+(MaxX(2)-MinX(2))*rand(Size,1);
E(:,3)=MinX(3)+(MaxX(3)-MinX(3))*rand(Size,1);%8-17代码就是在参数指定范围随机生成size组要优化的控制参数,产生种群E,后续的选择、复制、变异都是对该初始种群E进行处理
G=50;%迭代次数(次数少达不到最优值,次数多时间长)
BsJ=0;%目标函数值初始化为0
%*************** 开始运行***************
for kg=1:1:G
time(kg)=kg;%此处time为种群迭代次数
%****** Step 1 : 计算第kg代种群最小目标函数值 BestJ(kg) ******
for i=1:1:Size
x=E(i,:);
BsJ=GA_PID_Simulink_fitness(x,BsJ);%调用目标函数,输入种群E中的第一个个体x,该个体就是一组参数组成的向量;返回目标函数值BsJ。
BsJi(i)=BsJ;%将每一个个体(控制参数)在simulink中仿真,都会得到一个目标函数值,执行完for循环,所有控制参数依次带入simulink中仿真,得到的所有目标函数值存放在BsJi向量中。
end
[OderJi,IndexJi]=sort(BsJi); %将所有目标函数值从小到大排序,OderJi返回的是BsJi向量经过排序后的结果向量,IndexJi返回的是OderJi结果向量元素在BsJi中的下标(位置)
BestJ(kg)=OderJi(1);%找到目标函数值最小值
BJ=BestJ(kg);%将目标函数值最小值保存
Ji=BsJi+1e-10; %因为优化的目的是目标函数值越小越好,那么就会有0结果,适应度fi是目标函数值的导数,所以加上1e-10是为了防止分母为零报错。
fi=1./Ji;%求适应度
[Oderfi,Indexfi]=sort(fi); %将所有适应度值从小到大排序
Bestfi=Oderfi(Size); %找到适应度最大值
BestS=E(Indexfi(Size),:); %适应度最大对应的目标函数最小对应的参数(个体)是整个种群中最优的参数(个体),找到适应度最大值对应个体在种群中的位置(第Indexfi(Size)个),即可找出适应度最大值对应最优参数,并保存给 BestS变量
bfi(kg)=Bestfi;%保存第kg代种群的适应度最大值
kg %第kg代
BestS %第kg代群体中最优个体,也就是满足目标函数最小,对应的个体,个体就是三个参数(kp,ki,kd)组成的行向量
BJ %第kg代群体对应的目标函数最小值
%****** Step 2 : 选择和复制计算******
%都是固定套路不必研究,但种群E变量名要与之前的代码一致
fi_sum=sum(fi);
fi_Size=(Oderfi/fi_sum)*Size;
fi_S=floor(fi_Size); % Selecting Bigger fi value
r=Size-sum(fi_S);
Rest=fi_Size-fi_S;
[RestValue,Index]=sort(Rest);
for i=Size:-1:Size-r+1
fi_S(Index(i))=fi_S(Index(i))+1; % Adding rest to equal Size
end
k=1;
for i=Size:-1:1 % Select the Sizeth and Reproduce firstly
for j=1:1:fi_S(i)
TempE(k,:)=E(Indexfi(i),:); % 通过上述选择复制产生新的个体,进而形成新的种群
k=k+1; % k is used to reproduce
end
end
%************ Step 3 : 交叉计算 ************
%都是固定套路不必研究,但种群E变量名要与之前的代码一致
Pc=0.90;%交叉概率
for i=1:2:(Size-1)
temp=rand;
if Pc>temp %Crossover Condition
alfa=rand;
TempE(i,:)=alfa*E(i+1,:)+(1-alfa)*E(i,:);
TempE(i+1,:)=alfa*E(i,:)+(1-alfa)*E(i+1,:);
end
end
TempE(Size,:)=BestS;
E=TempE;%通过上述交叉产生新的个体,进而形成新的种群
%************ Step 4: 变异计算 **************
Pm=0.10-[1:1:Size]*(0.01)/Size; %(变异概率计算,每个个体变异概率不一样)Bigger fi,smaller Pm
Pm_rand=rand(Size,CodeL);
Mean=(MaxX + MinX)/2;
Dif=(MaxX-MinX);
for i=1:1:Size
for j=1:1:CodeL
if Pm(i)>Pm_rand(i,j) %Mutation Condition
TempE(i,j)=Mean(j)+Dif(j)*(rand-0.5);
end
end
end
%Guarantee TempE(Size,:) belong to the best individual
TempE(Size,:)=BestS;
E=TempE;%%通过上述变异产生新的个体,进而形成新的种群
end
%23-105代码实现G次迭代,迭代过程为计算当前种群最小目标函数,最大适应度,并找出对应的最优参数个体,然后对整个当前种群做选择、复制、交叉、变异,产生新的更好地种群,然后进行下一步迭代。
BestS %迭代完成后的种群里面的最优个体,也就是经过遗传寻优得到的最优参数向量
Bestfi %以经过迭代产生的最优参数,运行simulink模型,计算目标函数,再计算适应度,得到的最大适应度值
fi %以经过迭代后的种群所有个体(包括最优个体)运行simulink模型,计算目标函数,再计算适应度,得到所有适应度值
x %经过迭代后种群的最后一个个体(不一定是最优个体)
Best_J=BestJ(G)%以第G代群体中个体,运行simulink模型,计算目标函数,其中的目标函数最小值
figure(1);
plot(time,BestJ);%注意此处的time不是时间,而是迭代次数,所以此处作图以迭代次数为横坐标,迭代次数对应群体的最小目标函数值为纵坐标
xlabel('Times');ylabel('Best J');
完整程序:
基于遗传算法的simulink/PID参数整定(s函数)_simulink遗传算法整定pid-电子商务文档类资源-CSDN文库
仿真结果:
迭代50次,需等待几分钟。
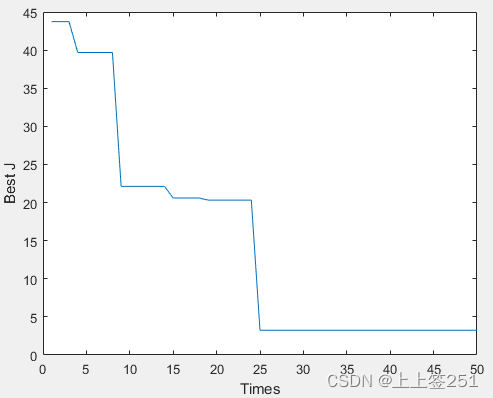
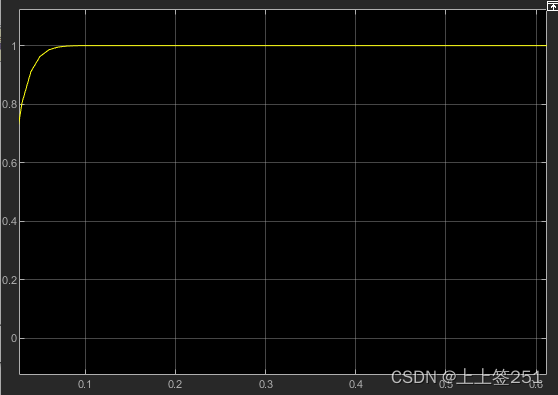
最后
以上就是沉默魔镜最近收集整理的关于基于遗传算法的simulink/PID参数整定(s函数)的全部内容,更多相关基于遗传算法内容请搜索靠谱客的其他文章。








发表评论 取消回复