基于遗传算法的PID参数整定研究
基于遗传算法的PID参数整定研究(七-九)是基于精确的传递函数进行优化,其本质是将优化对象简化为一阶或者二阶的传递函数,在.m程序上进行编写其零极点模型,从而应用遗传算法对其进行参数整定。
然而,实际情况是大多数的被控对象往往其传递函数难以获得,无法运用经典控制理论进行合理化的模型建立。比如针对含有SVPWM的双闭环矢量控制系统,含离散元器件的系统,以及非线性的单元等等。因此,有必要建立一种直接联合Simulink仿真模型的在线参数整定。
1.3.4遗传算法联合Simulink仿真下的参数整定
当被控对象为双闭环矢量PI控制系统,采取实数编码优化的三个决策变量分别为kP,ki,Ba,使用的样本个数为5,交叉概率和变异概率分别为:Pc=0.9,Mu=0.033。设定优化区间分别为:参数kP的取值范围为[0,1],ki的取值范围为[0,7],Ba的取值范围为[0,0.02]。经过5代进化,获得的优化参数如下:
kP=0.1317,ki=1.4187,Ba=0.0035,性能指标J=0.0342,整定过程中代价函数J的变化如图15所示。优化后空载工况下的转速响应波形如图16所示。
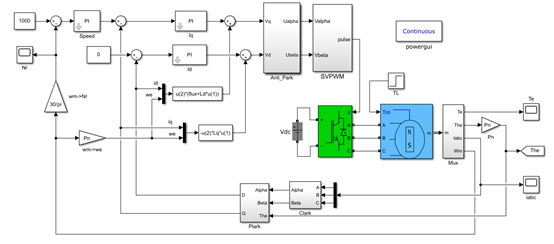
图14 永磁同步电机的双闭环矢量PI控制系统
主函数 main.m
clc,
clear all; %#ok<CLALL>
tic %计时开始
global w1 w2 yout ycrtl simout1
%% 电机参数设定
Ts = 1e-5;
Pn = 4;
flux = 0.1827;
R = 0.9585;
Ld = 0.00525;
Lq = 0.00525;
J = 0.0006329;
%0.221515
B = 0.0003035;
Kt = 1.5*Pn*flux;
%% 遗传算法优化参数
Size=5;
% 种群大小30个 可行解
G=5;
% 种群运行100次
CodeL=3;
% 三个实数编码 三个决策变量
rin = 1000.0000; %控制输入
B=0;
% rand('state',sum(clock));
MinX(1)=zeros(1);
MaxX(1)=1*ones(1);
MinX(2)=0*ones(1);
MaxX(2)=7*ones(1);
MinX(3)=0*ones(1);
MaxX(3)=0.02*ones(1);
Kpid(:,1)=MinX(1)+(MaxX(1)-MinX(1))*rand(Size,1);
Kpid(:,2)=MinX(2)+(MaxX(2)-MinX(2))*rand(Size,1);
Kpid(:,3)=MinX(3)+(MaxX(3)-MinX(3))*rand(Size,1);
BsJ=0;
%*************** Start Running ***************
for kg=1:1:G
time(kg)=kg;
%****** Step 1 : Evaluate BestJ ******
for i=1:1:Size
Kpidi=Kpid(i,:);
%单个可行解
Kp = Kpidi(1);
%反馈d-q轴电流
Ki = Kpidi(2);
Ba = Kpidi(3);
clc,
simout1 = sim('PMSM_PI_decomposition');
% 时间输出
clc,
%目标函数
P = length(simout1);
yout
= w1;
%转速反馈值
ycrtl = w2;
%转速控制输入
error = yout-rin;
%转速偏差
A = roundn(yout,-4); %一维数组
num = round(P*0.618);
ymax = max(A); %最大值
Value =roundn(mean(yout(num:P-1,1)),-4);%一个数值
%% 上升时间
[row1 col1]=find(ymax==A);
tu1=simout1(row1);
%% 调节时间,允许的误差范围内
%
[row2 col2]=find(rin==A);
%
tu2=simout1(row2);
%% 误差调节
%
B=0.001*sum(abs(error(num)));
%
for i=1:1:P
%
if i>1
%
erry(i)=w1(i)-w1(i-1);
%
if erry(i)<0
%
B=B+100*(abs(erry(i)));
%
end
%
end
%
end
BsJ=B+(tu1)*10;
%
[Kpidi,BsJ]=chap_f1(Kpidi,BsJ);
BsJi(i)=BsJ;
%%BsJi优化参数的数值矩阵
end
[OderJi,IndexJi]=sort(BsJi);
BestJ(kg)=OderJi(1);
BJ=BestJ(kg);
Ji=BsJi+1e-10;
%Avoiding deviding zero
fi=1./Ji;
%
Cm=max(Ji);
%
fi=Cm-Ji;
[Oderfi,Indexfi]=sort(fi);
%Arranging fi small to bigger
Bestfi=Oderfi(Size);
%Let Bestfi=max(fi)
BestS=Kpid(Indexfi(Size),:);
%Let BestS=E(m), m is the Indexfi belong to max(fi)
kg
BJ
BestS
%****** Step 2 : Select and Reproduct Operation******
fi_sum=sum(fi);
fi_Size=(Oderfi/fi_sum)*Size;
fi_S=floor(fi_Size);
% Selecting Bigger fi value
r=Size-sum(fi_S);
Rest=fi_Size-fi_S;
[RestValue,Index]=sort(Rest);
for i=Size:-1:Size-r+1
fi_S(Index(i))=fi_S(Index(i))+1;
% Adding rest to equal Size
end
k=1;
for i=Size:-1:1
% Select the Sizeth and Reproduce firstly
for j=1:1:fi_S(i)
TempE(k,:)=Kpid(Indexfi(i),:);
% Select and Reproduce
k=k+1;
% k is used to reproduce
end
end
%************ Step 3 : Crossover Operation ************
Pc=0.90;
for i=1:2:(Size-1)
temp=rand;
if Pc>temp
%Crossover Condition
alfa=rand;
TempE(i,:)=alfa*Kpid(i+1,:)+(1-alfa)*Kpid(i,:);
TempE(i+1,:)=alfa*Kpid(i,:)+(1-alfa)*Kpid(i+1,:);
end
end
TempE(Size,:)=BestS;
Kpid=TempE;
%************ Step 4: Mutation Operation **************
Pm=0.10-[1:1:Size]*(0.01)/Size;
%Bigger fi,smaller Pm
Pm_rand=rand(Size,CodeL);
Mean=(MaxX + MinX)/2;
Dif=(MaxX-MinX);
for i=1:1:Size
for j=1:1:CodeL
if Pm(i)>Pm_rand(i,j)
%Mutation Condition
TempE(i,j)=Mean(j)+Dif(j)*(rand-0.5);
end
end
end
%Guarantee TempE(Size,:) belong to the best individual
TempE(Size,:)=BestS;
Kpid=TempE;
end
Bestfi
BestS
Best_J=BestJ(G)
figure(1);
plot(time,BestJ);
xlabel('Times');ylabel('Best J');
% figure(2);
% plot(timef,rin,'r',timef,yout,'b');
% xlabel('Time(s)');ylabel('rin,yout');
toc %计时结束
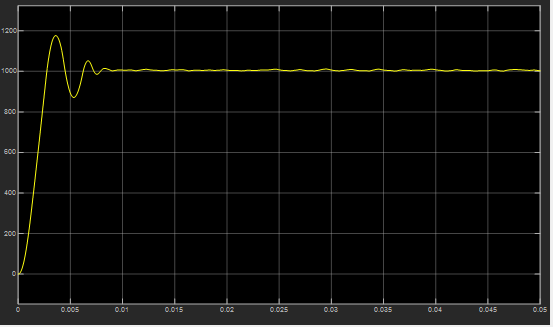
图15 优化前空载工况下的转速响应波形
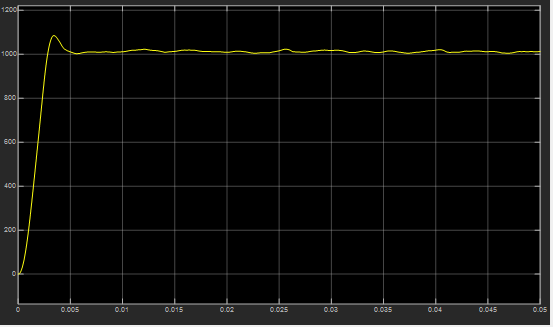
图16 优化后空载工况下的转速响应波形
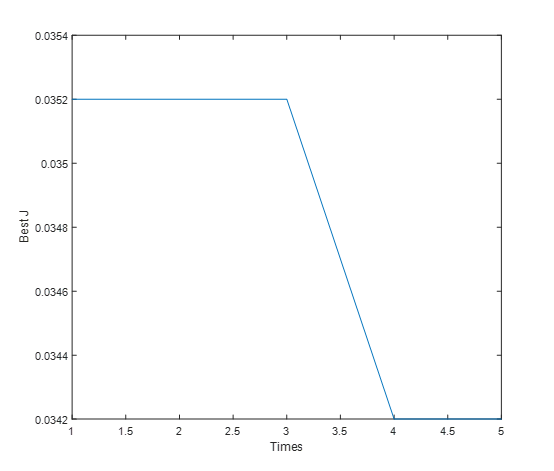
图17 代价函数J的变化过程
由图15和图16可知,优化后的性能对比,超调明显减小,但是稳态性能却变差了,因此对于处于矛盾性质的性能指标无法做到二者兼得。因此,可以运用多目标优化算法对其进行改进并进行在线参数整定。
最后
以上就是天真皮卡丘最近收集整理的关于基于遗传算法的PID参数整定研究(十)——GA算法联合Simulink仿真下的参数整定的全部内容,更多相关基于遗传算法内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复