目录
MATLAB二维曲线及二维图形
1-plot(x,y)函数的基本用法
2-fplot(f,lim,选项)函数的基本用法
3-subplot(m,n,p)函数的基本用法
4- polar(theata,rho,选项)函数的基本用法
5-bar(y,style)函数的基本用法
6-hist(y,x)函数和rose(theta,x)函数的基本用法
7-pie(x,explode)函数和area()函数的用法
8-scatter()函数、stairs()函数、stem()函数的应用
9-compass()函数、feather()函数、quiver()函数的应用
MATLAB二维曲线及二维图形
1-plot(x,y)函数的基本用法
plot(x,y)函数的基本用法:其中分别用于存储x坐标和y的坐标。
我们看一下例子1,用plot函数绘制一条折线。代码如下:
x = [2.5, 3.5, 4, 5] ;
y = [1.5, 2.0, 1, 1.5] ;
plot(x,y);绘制的折线图如下所示:
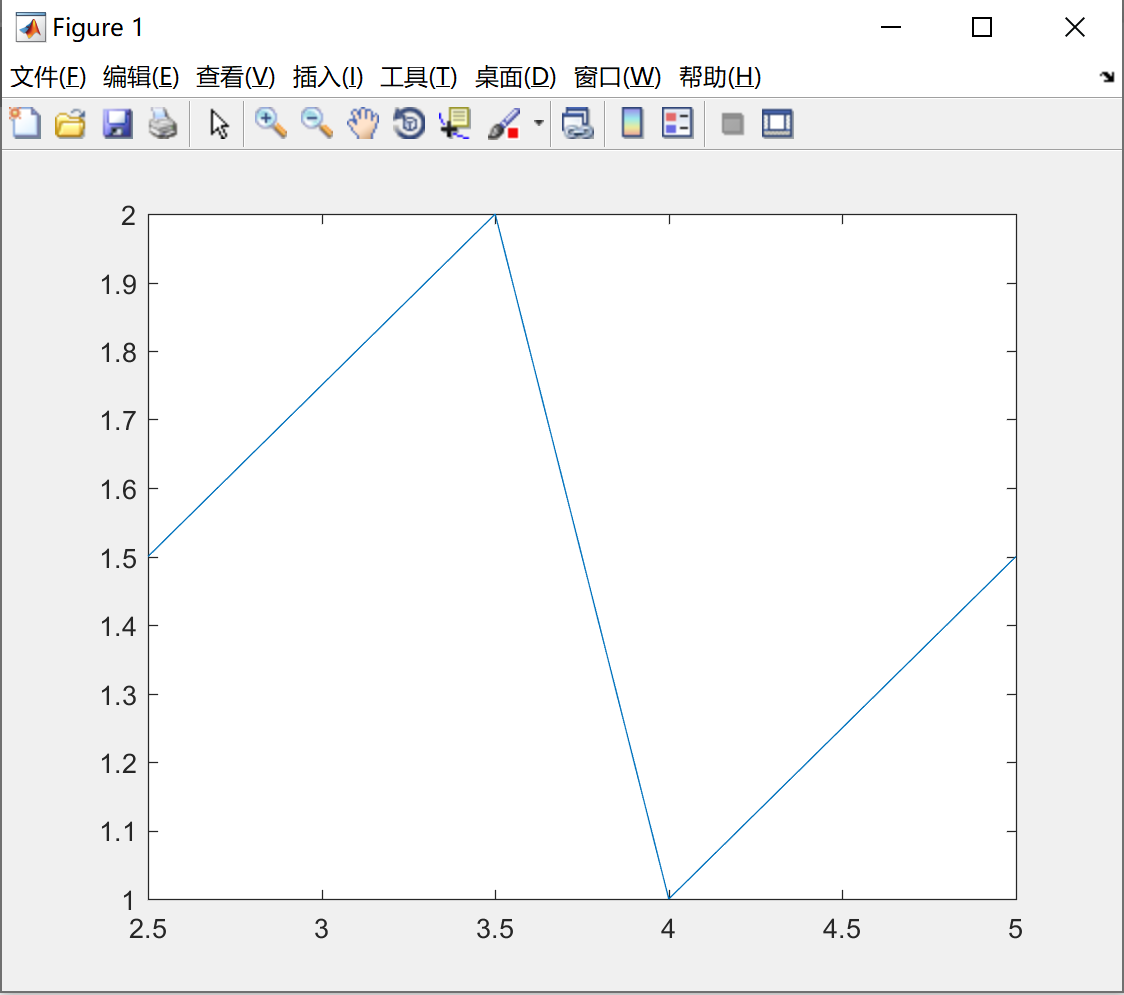
如果plot()函数中只有参数x,则x作为纵坐标,x对应的位置作为横坐标。
如下代码的横坐标是1,2,3,4,纵坐标为向量x中的值。
x = [2,3,4,5] ;
plot(x) ;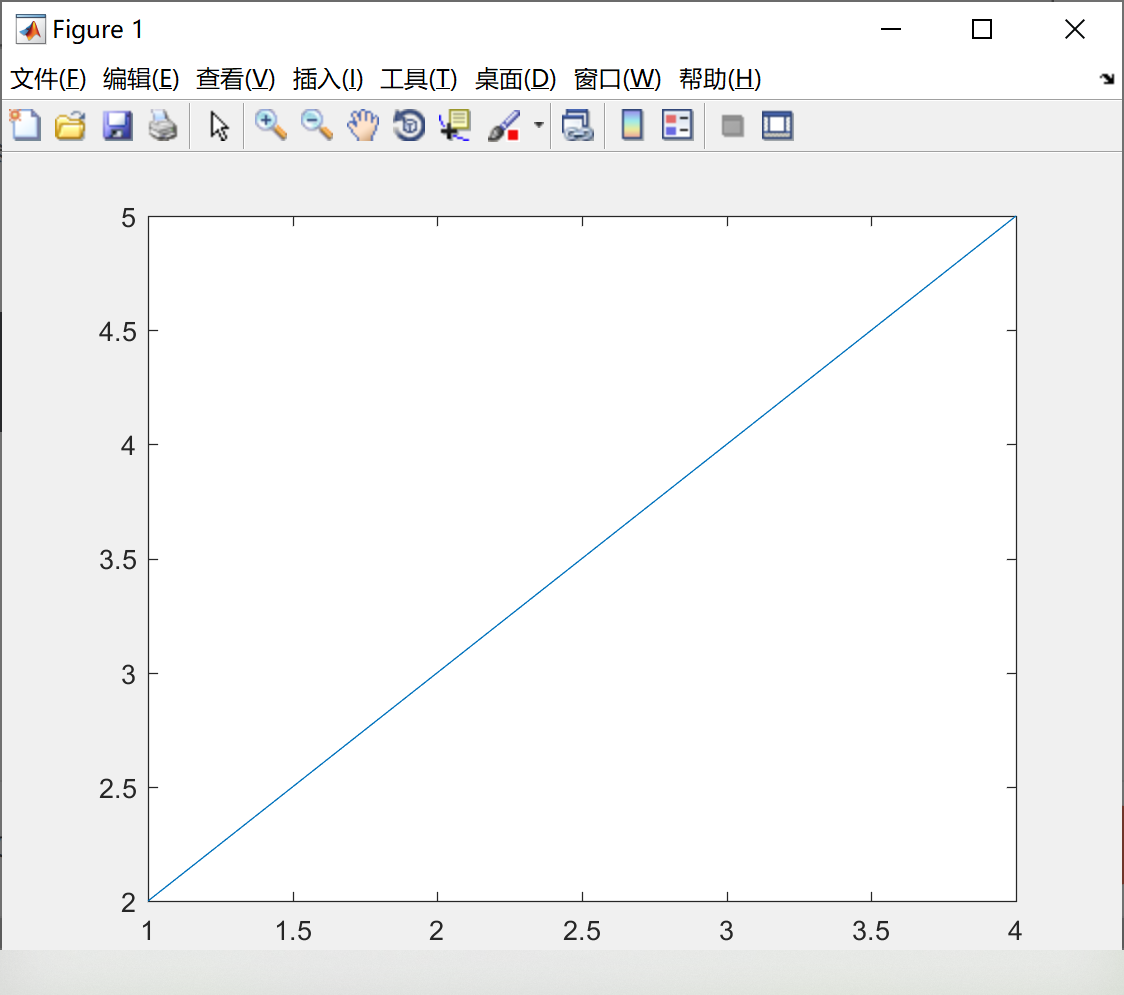
当plot函数的参数x是复数向量的时候,分别以该向量元素的实部和虚部作为横纵坐标,绘制一条折线。
x = [2.5, 3.5, 4, 5] ;
y = [1.5, 2, 1, 1.5] ;
cx = complex(x,y) ;
plot(cx) ;绘制的图形如下所示:
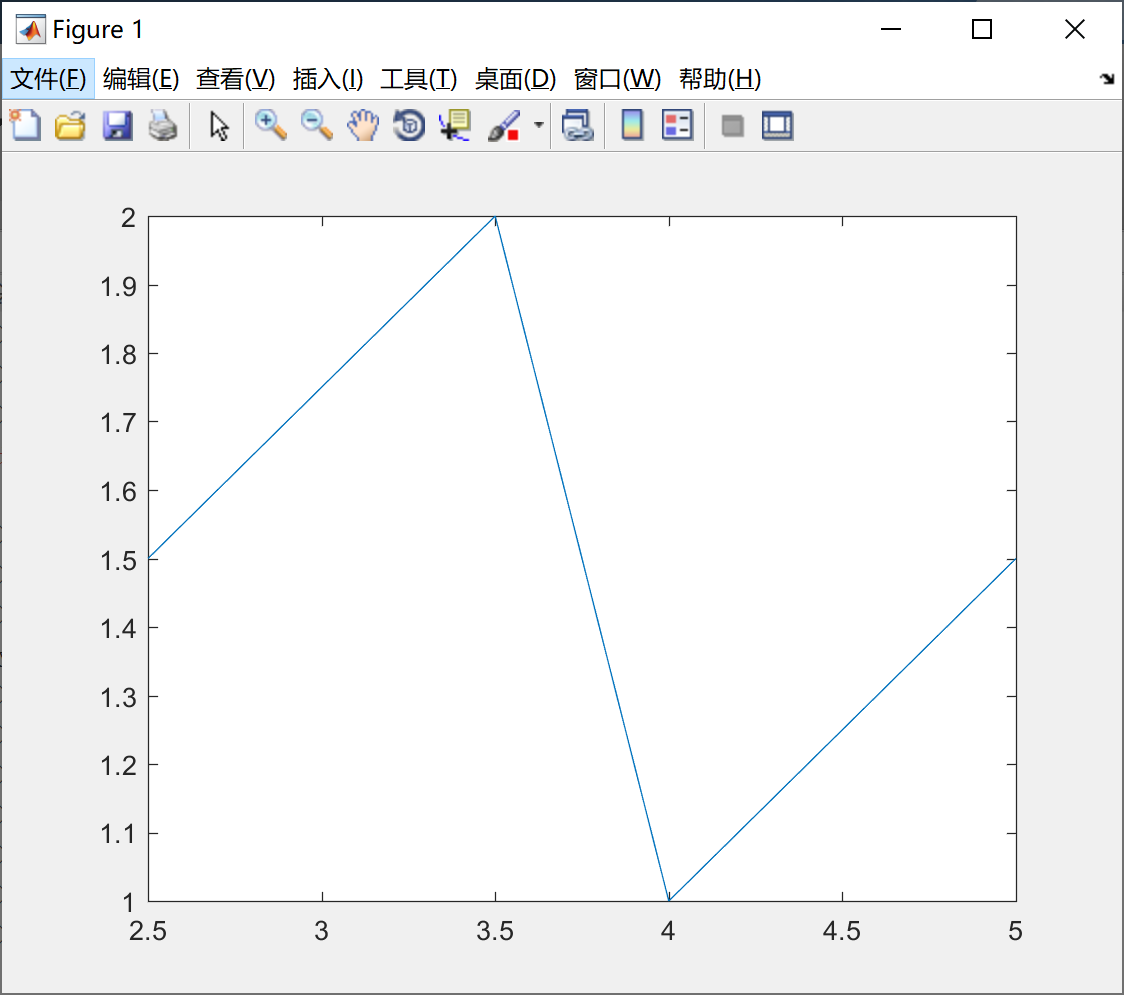
plot(x,y)函数参数的变化形式:
当x是向量,y是矩阵时,如果矩阵y的列数等于x的长度,则以向量x的为横坐标,以y的每个行向量为纵坐标绘制曲线,曲线的条数等于y的行数。
如果矩阵y的行数等于x的长度,则以向量x为横坐标,以y的每个列向量为纵坐标绘制曲线,曲线的条数等于y的列数。
看一下例子2,矩阵y的行向量与行向量x的长度相同,代码如下:
x = linspace(0,2*pi,100) ;
y = [sin(x); sin(2*x); sin(0.5*x)] ;
plot(x,y) ;绘制的图形如下所示:
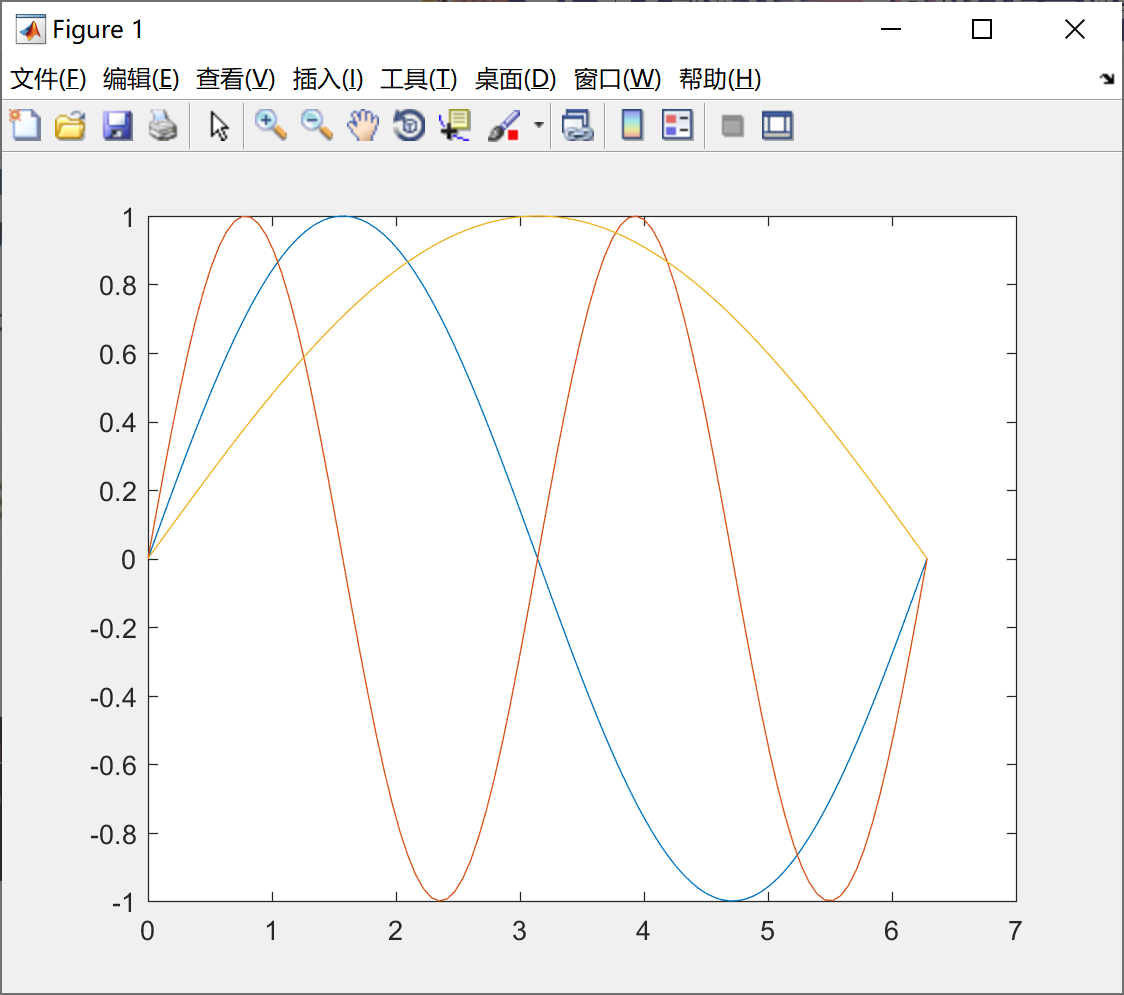
上述代码也可以写成入戏的形式,代码如下:
t = 0 : 0.01 : 2*pi ;
t1 = t' ;
x = [t1, t1, t1];
y = [sin(t1),sin(2*t1),sin(0.5*t1)] ;
plot(x,y) ;
含有多个输入的plot()函数,使用向量对的方式,每个向量对构成 一组数据的横纵坐标,绘制出图形。
看一下例子3,我们使用10个,20个,100个数据点绘制正弦曲线,会发现数据点越多曲线越光滑。代码如下所示:
t1 = linspace(0,2*pi,10) ;
t2 = linspace(0, 2*pi, 20) ;
t3 = linspace(0, 2*pi, 100) ;
plot(t1,sin(t1),t2,sin(t2)+1,t3,sin(t3)+2) ;
绘制的图形入下所示:
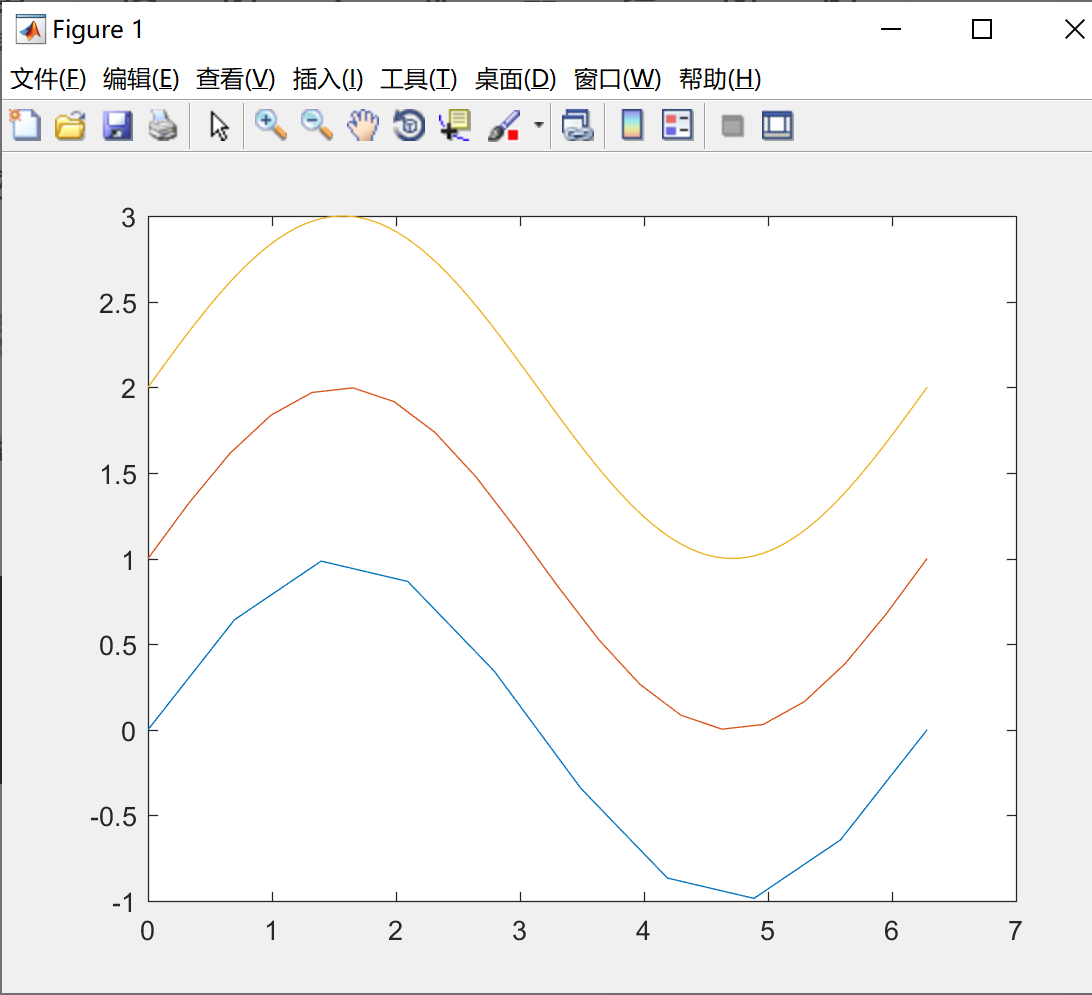
含选项的plot函数,plot(x,y,选项)函数,选项用于指定线型,颜色,数据点标记。
线型有如下几种常用的:
“-” :实线 “:”:虚线 “-.”:点画线 “--”双画线
颜色一般用英文的首字母字母开头,例如:
“r” :红色 “g”:绿色 “b”:蓝色 “w”:白色 “k”:黑色
数据点标记常用的如下所示:
“*” :星号 “o”:圆圈 “s”:方形 “p”:五角星 “^”:朝上三角形 ‘d’:菱形
我们看一下上面的例子4,代码如下所示:
x = (0:pi/50:2*pi)' ;
y1 = 2 * exp(-0.5*x)*[1,-1];
y2 = 2 * exp(-0.5*x).*sin(2*pi*x);
x1 = 0:0.5:6 ;
y3 = 2 * exp(-0.5*x1).*sin(2*pi*x1) ;
plot(x,y1,'k:',x,y2,'b--',x1,y3,'rp') ;绘制的图形如下所示:
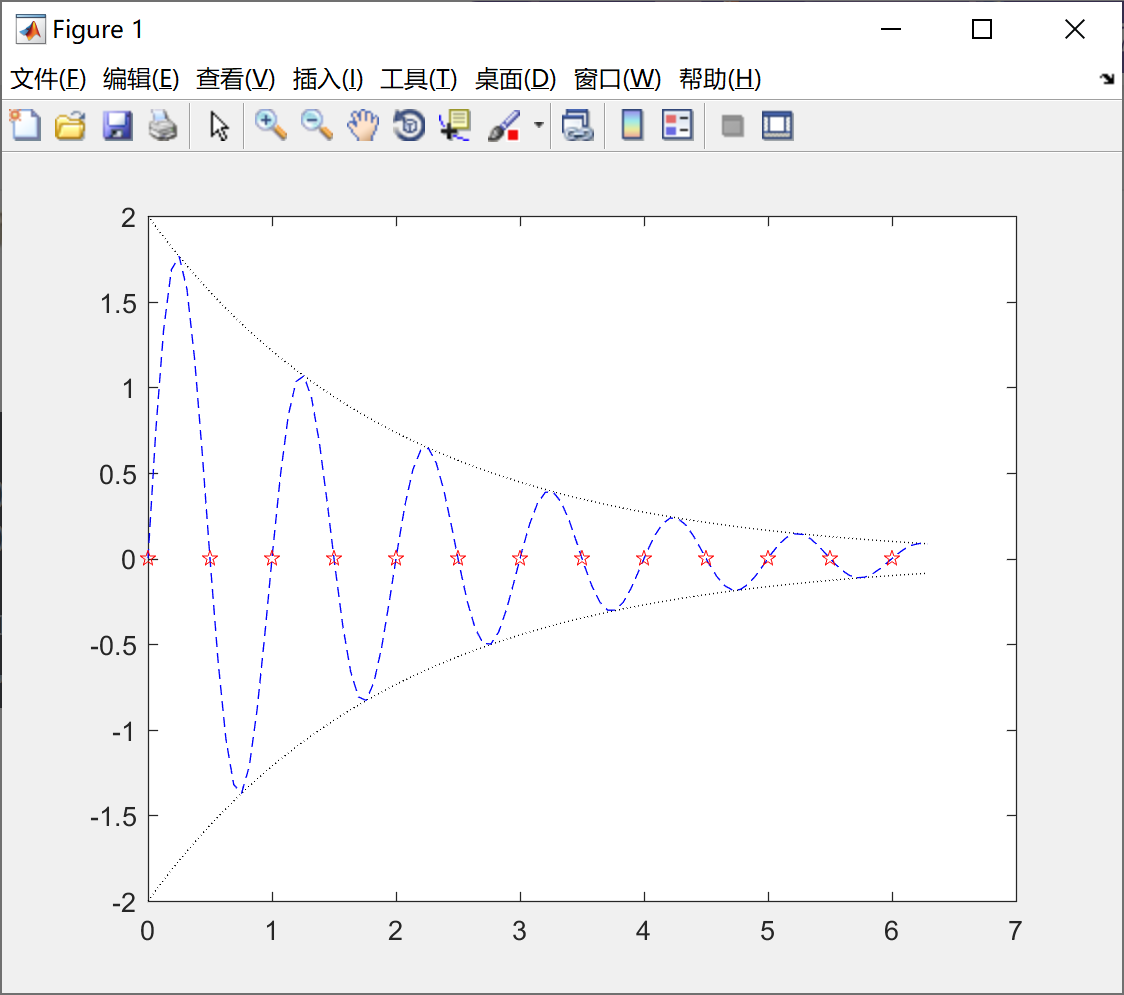
2-fplot(f,lim,选项)函数的基本用法
自适应设置间隔绘图的函数fplot(f,lim,选项),自适应间隔,一般波动变化较大的间隔设大一些,波动变化较小的,间隔设置小一点。其中f代表一个函数,通常采用函数句柄的形式,lims表示x轴的取值范围,用二元向量[xmin,xmax]表示,默认为[-5,5],选项部分与plot()函数相同。
我们看一下上面例子6,具体的代码如下:
fplot(@(x) sin(1./x), [0,0.2], 'b') ;绘制的图形如下所示:
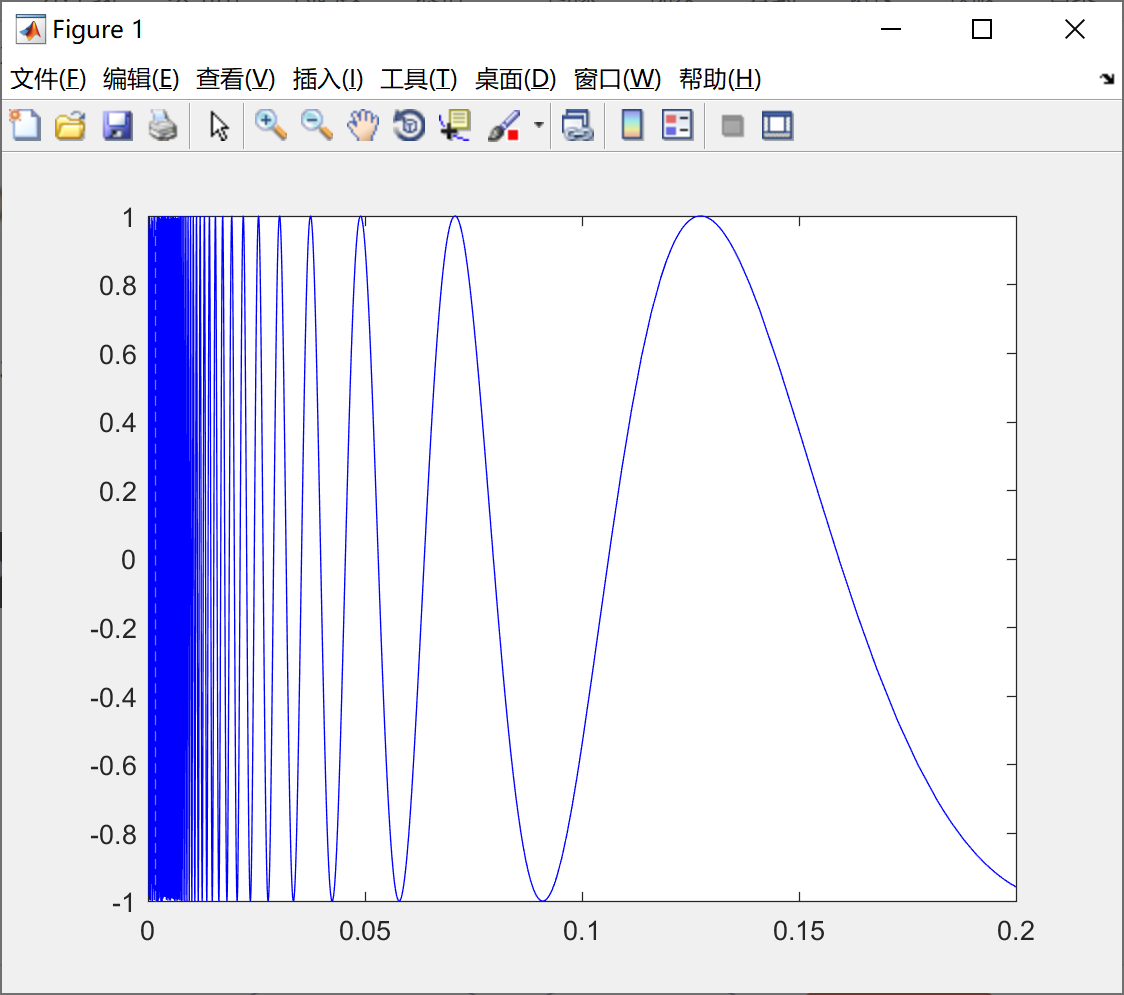
双输入函数参数的用法:fplot(funx,funy,tlims,选项)
我们看一下上面的例子,具体的代码如下所示:
fplot(@(t) t.*sin(t), @(t) t.*cos(t), [0, 10*pi], 'r') ;
绘制的图形如下所示:
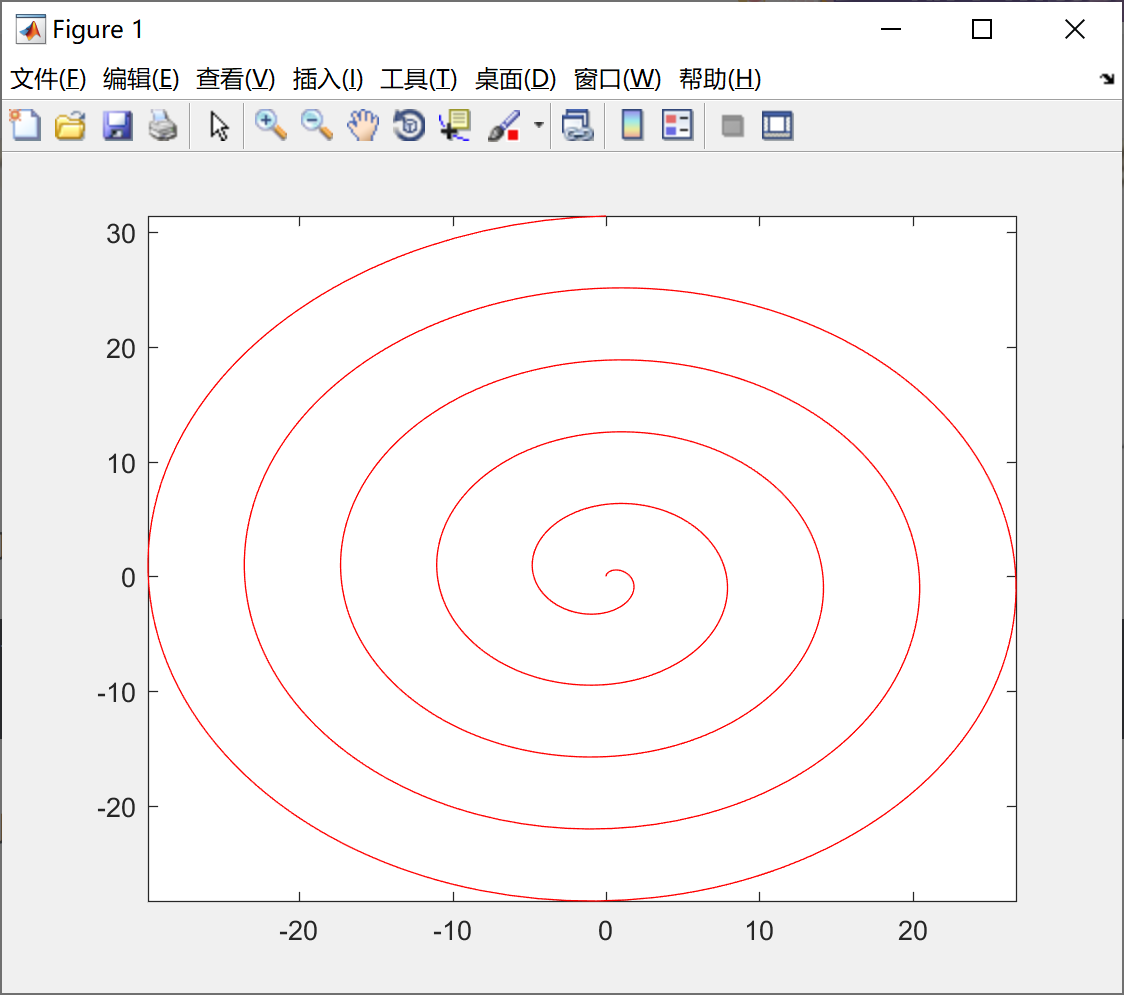
绘制图形的辅助操作
图形标注包括:title(图形标题),xlabel(x轴说明),ylabel(y轴说明),text(x,y,图形说明),legend(图例1,图例2,...)
我们看一下上面的例子1,绘制图形并添加标题,代码入下:
x = -2*pi : 0.05 : 2*pi ;
y = sin(x) ;
plot(x,y) ;
title('y=sinx') ;绘制的图形如下所示:
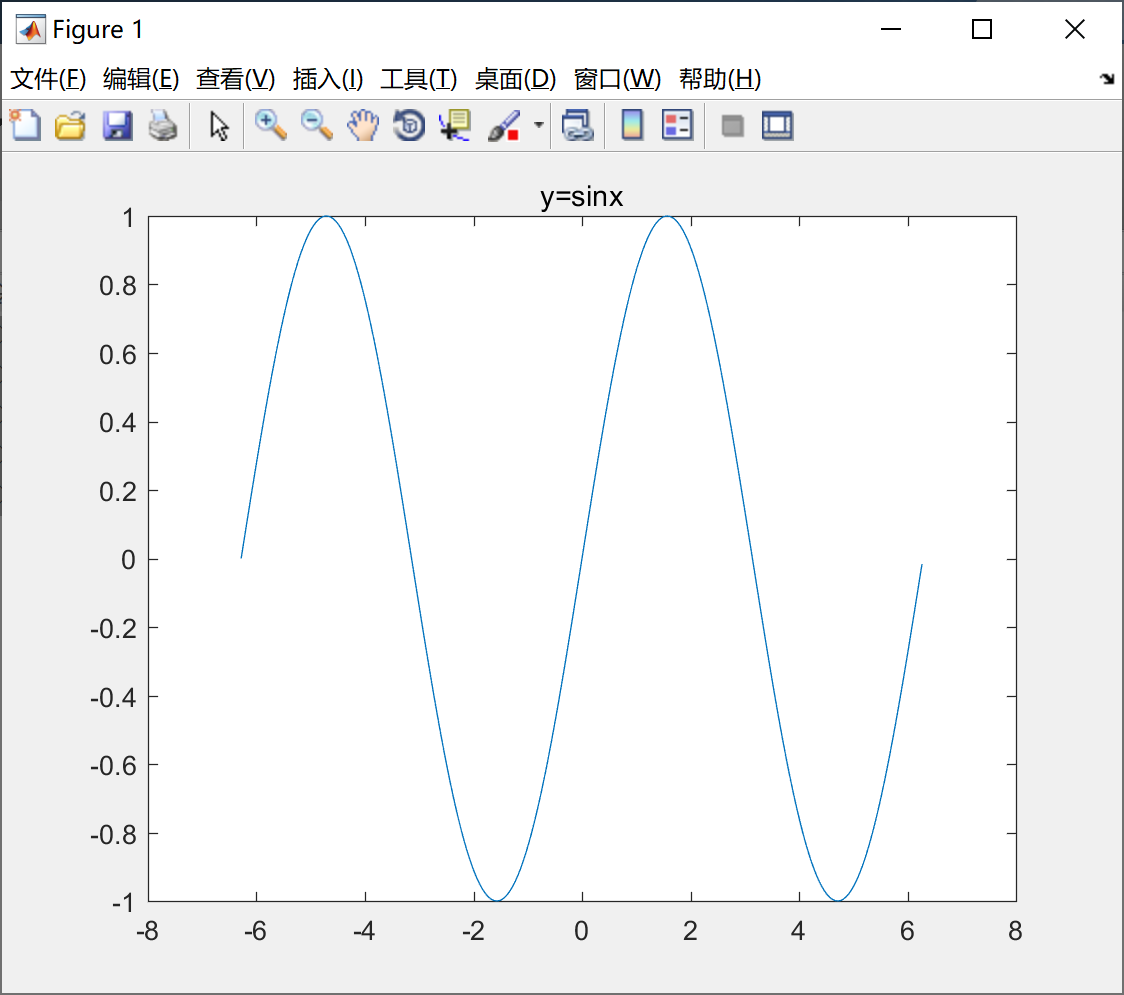
在图形标题中使用Latex格式控制符。
含有属性的title(图形标题,属性名,属性值):其中Color属性设置标题颜色,FrontSize属性设置标题大小。
xlabel(x轴说明)
ylabel(y轴说明)
下面我们绘制sinx的函数,并添加标题和标签,代码如下:
x = -2*pi : 0.05 : 2*pi ;
>> y = sin(x) ;
>> plot(x,y) ;
>> title('y=sinx') ;
>> xlabel('-2pileqxleq2pi') ;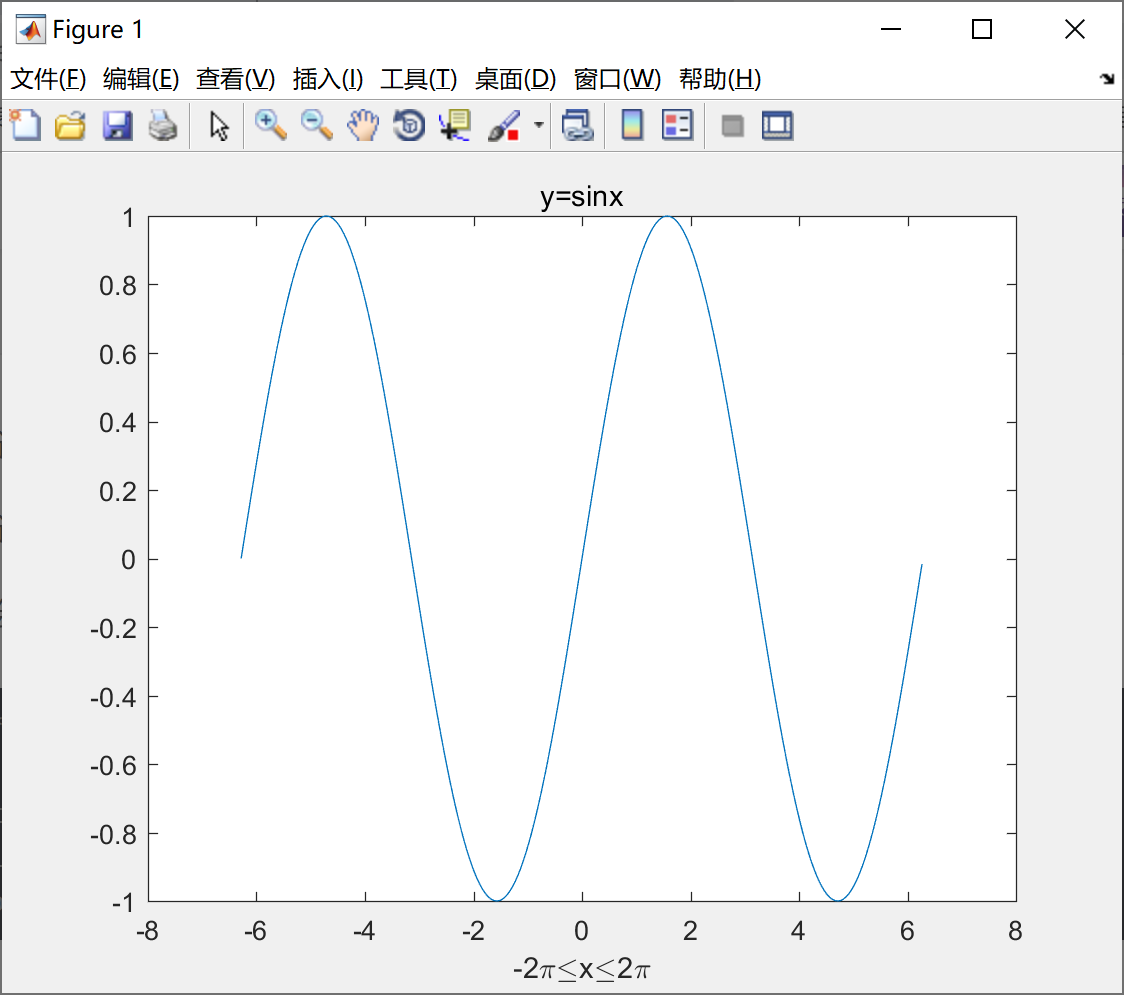
legend(图例1,图例2,...)
我们看一下例子2,关于legend()函数的使用,代码入下:
x = linspace(0, 2*pi, 100) ;
plot(x,[sin(x); sin(2*x); sin(3*x)]) ;
legend('sin(x)', 'sin(2x)', 'sin(3x)') ;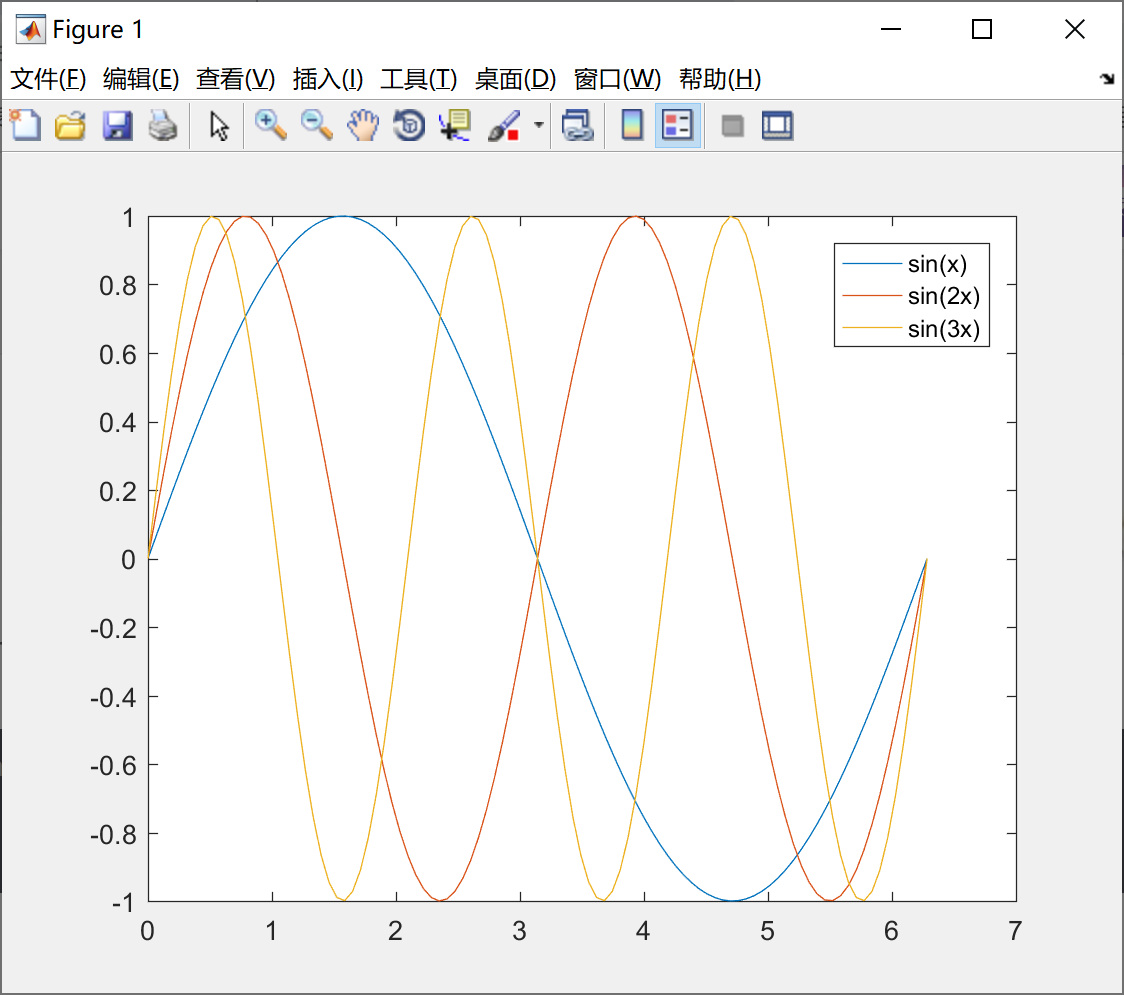
坐标控制,一般使用axis([xmin,xmax,ymin,ymax,zmin,zmax]) 函数来实现。这是三维的了,两维的只需要x和y就够了。
我们看一个画正方形的例子,代码如下所示:
x = [0,1,1,0,0] ;
y = [0,0,1,1,0] ;
plot(x,y) ;
axis([-0.1,1.1,-0.1,1.1]) ;
axis equal ; %设置横纵坐标轴采用等行刻度绘出的图形如下所示:
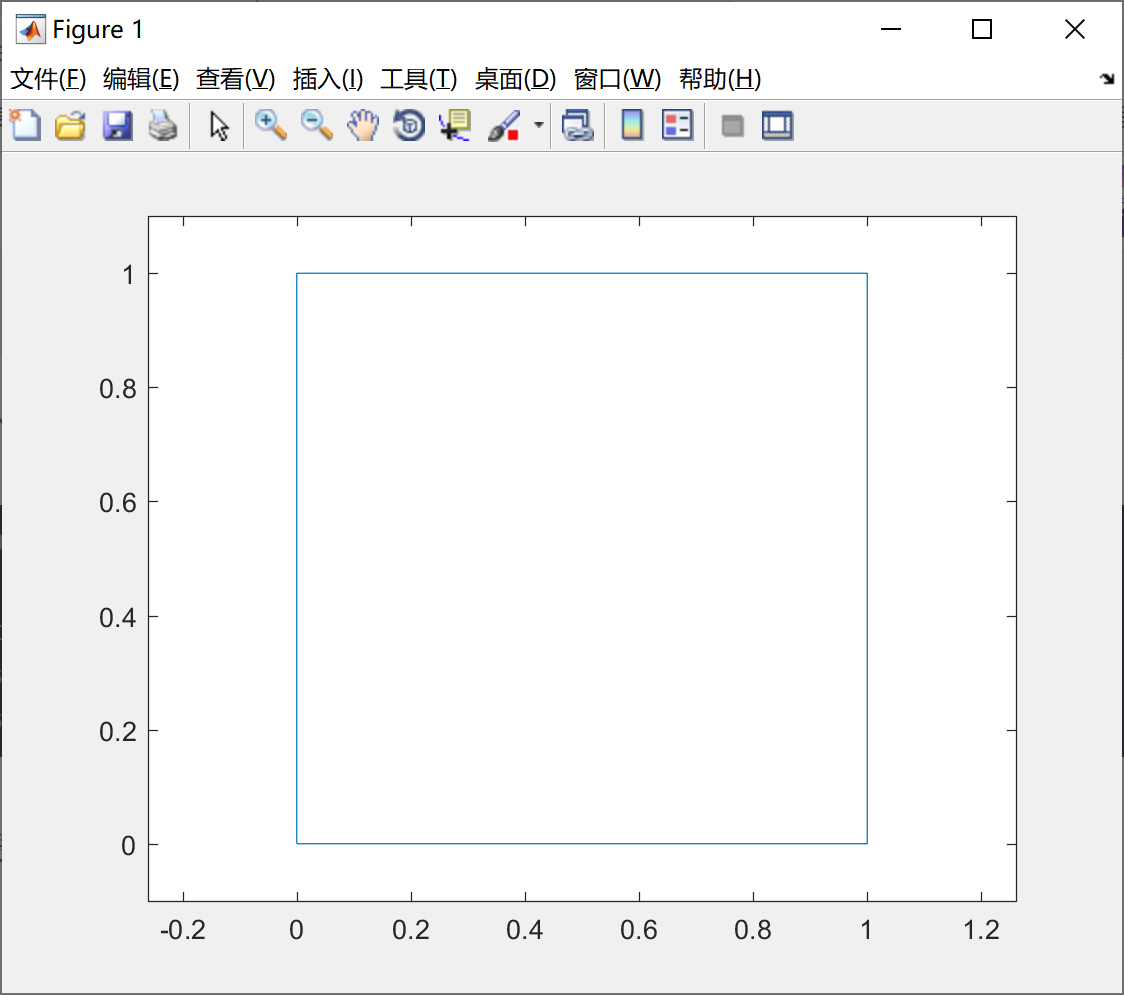
给坐标系加网格线命令:grid on ,给坐标系加边框,box on 命令。
我们看一下例子3,通过例子3对图形标注命令进行复习,代码如下所示:
x = linspace(0,2*pi,100) ;
y = [sin(x); sin(2*x); sin(0.5*x)] ;
plot(x,y) ;
axis([0,7,-1.2,1.2]) ;
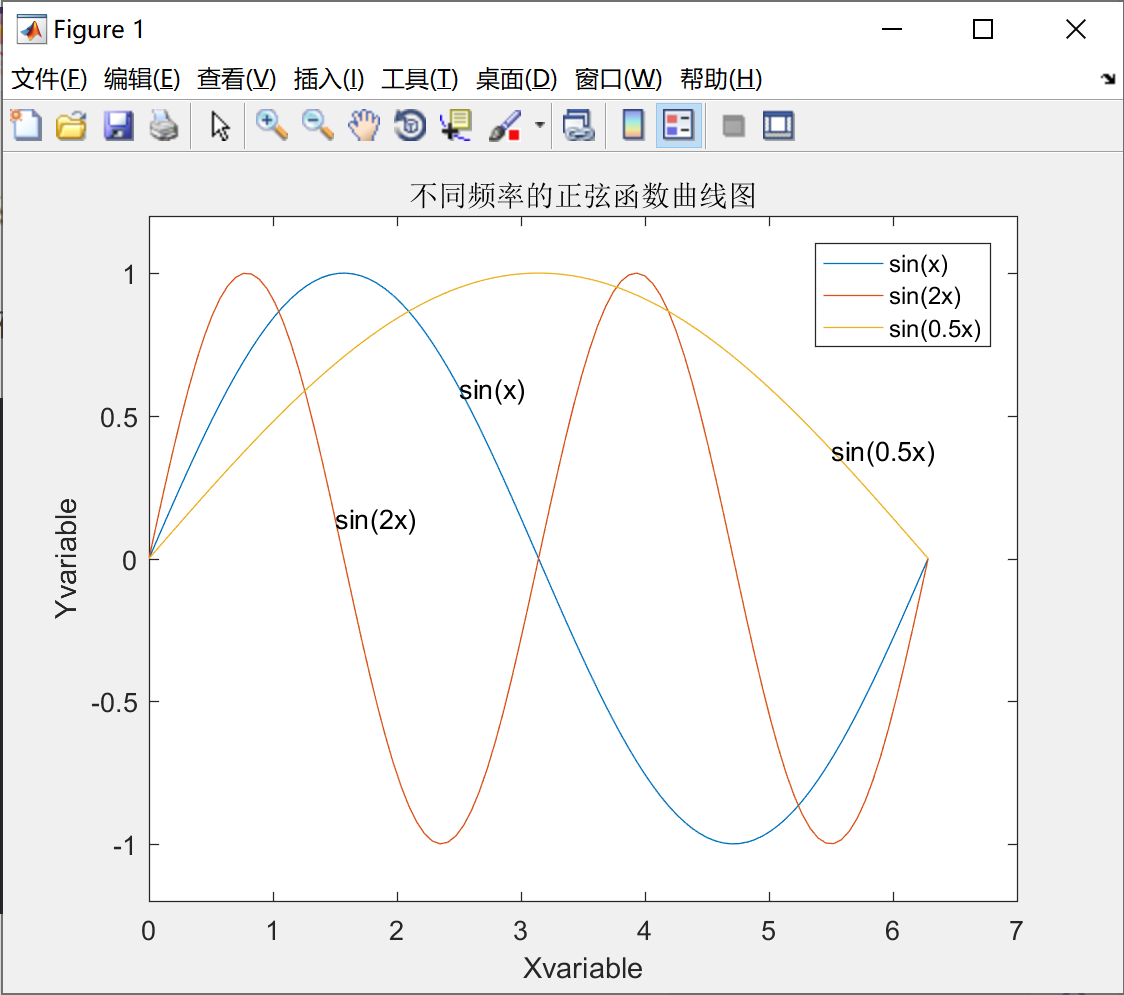
title('不同频率的正弦函数曲线图') ;
xlabel('Xvariable') ;
ylabel('Yvariable') ;
text(2.5, sin(2.5), 'sin(x)') ;
text(1.5, sin(2*1.5), 'sin(2x)') ;
text(5.5, sin(0.5*5.5), 'sin(0.5x)') ;
legend('sin(x)','sin(2x)','sin(0.5x)') ;绘制的图形如下所示,图中有标题,标签,图例等标注。
hold on 命令保持原图形窗口,hold off命令刷新图形窗口,hold命令在两种命令之间切换。
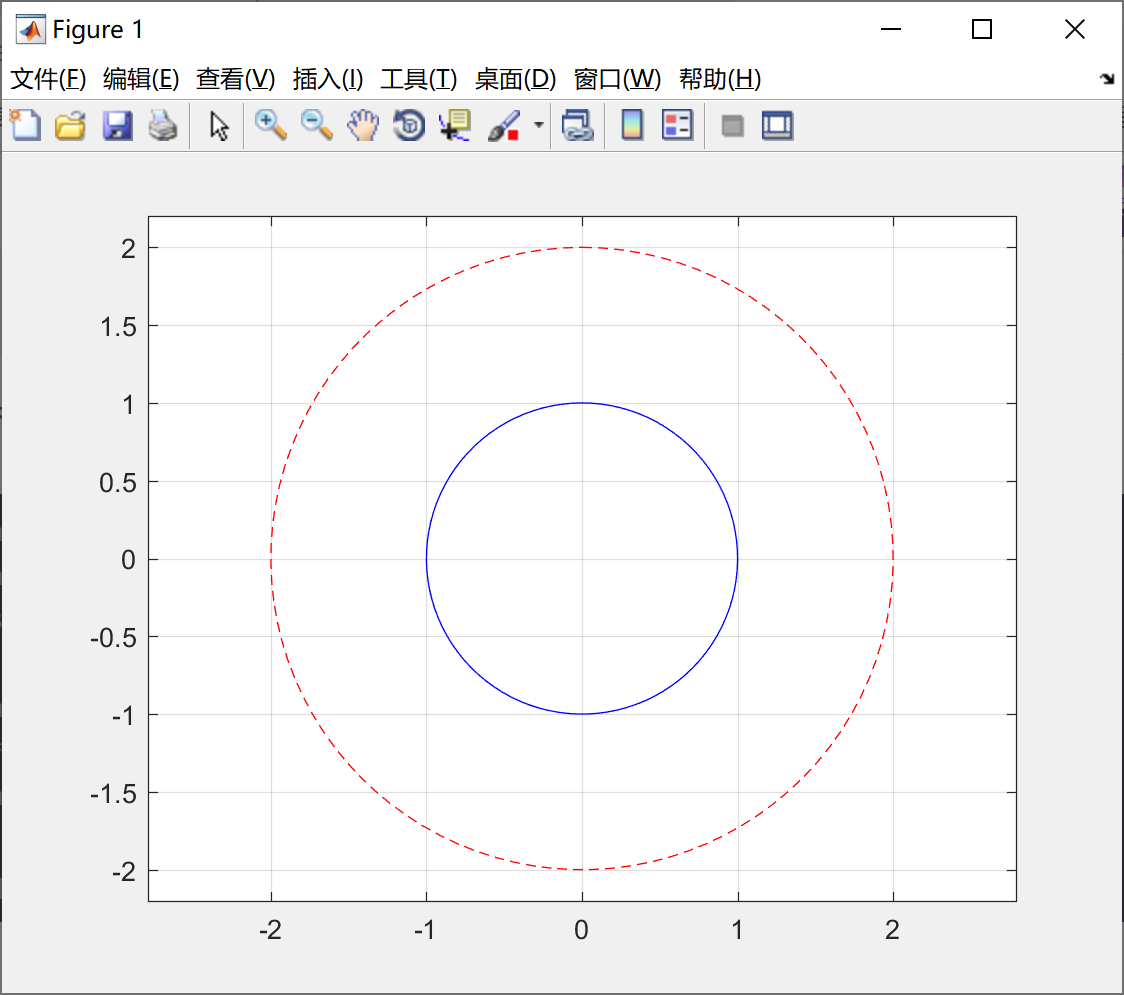
我们看一下上面的例子4,使用图形保持功能在一幅图中绘制两个同心圆,代码如下所示:
t = linspace(0, 2*pi, 100) ;
x = sin(t) ;
y = cos(t) ;
plot(x,y,'b') ;
hold on ;
plot(2*x,2*y,'r--') ;
grid on ;
axis([-2.2,2.2,-2.2,2.2]) ;
axis equal ;绘制的图形如下所示:
3-subplot(m,n,p)函数的基本用法
图形窗口的分割:同一窗口中不同坐标系下的图形称为子图,使用subplot(m,n,p)函数,代表划分成m*n个窗口,并在第p个窗口绘图。
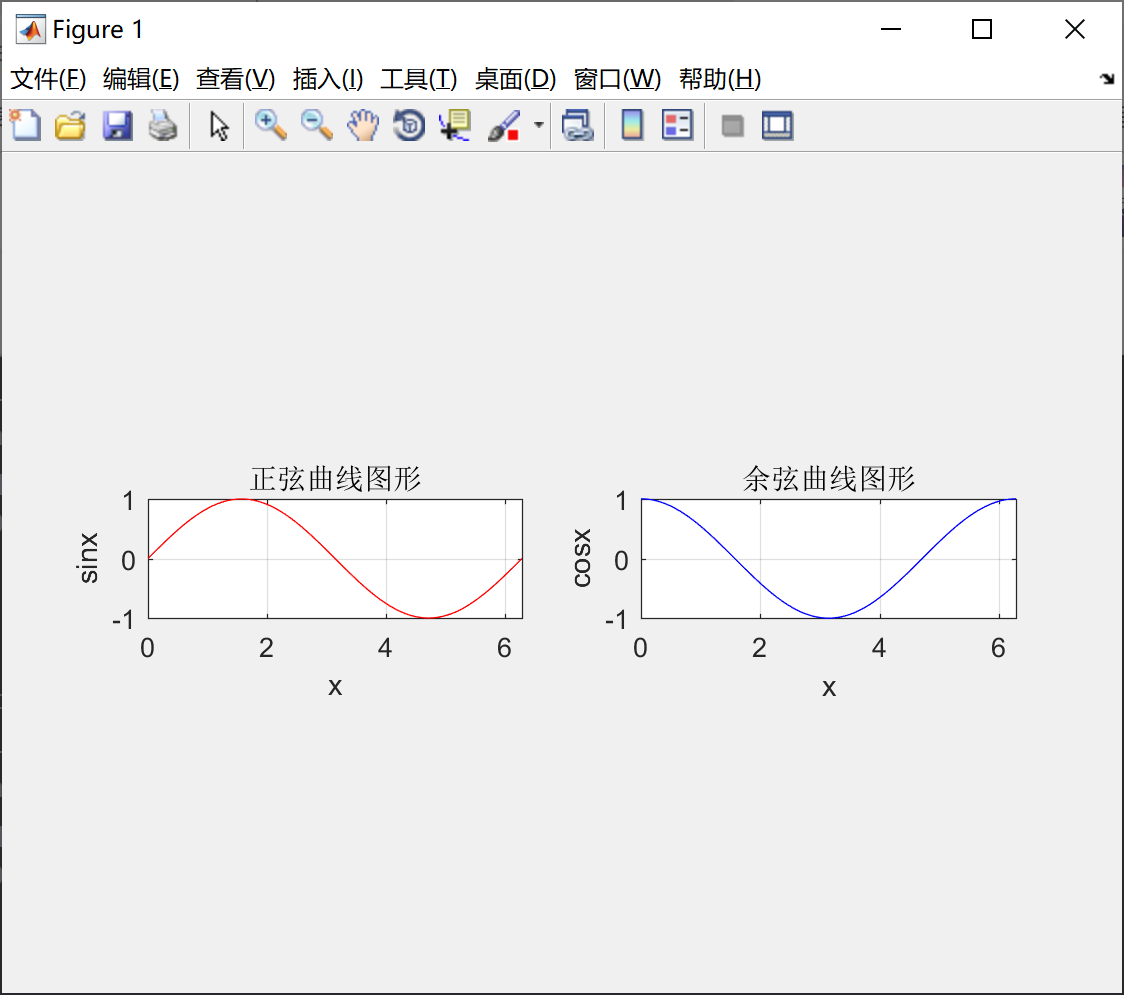
把正弦函数和余弦函数花在一个图中,代码如下所示:
x1 = linspace(0,2*pi,100) ;
subplot(1,2,1) ;
plot(x1, sin(x1), 'r') ;
grid on ;
axis equal ;
axis([0, 2*pi, -1, 1]) ;
title('正弦曲线图形') ;
xlabel('x') ;
ylabel('sinx') ;
subplot(1,2,2);
plot(x1, cos(x1), 'b') ;
grid on ;
axis equal ;
axis([0, 2*pi, -1, 1]) ;
title('余弦曲线图形') ;
xlabel('x') ;
ylabel('cosx') ;绘制的图形如下所示:
其它形式的二维曲线:
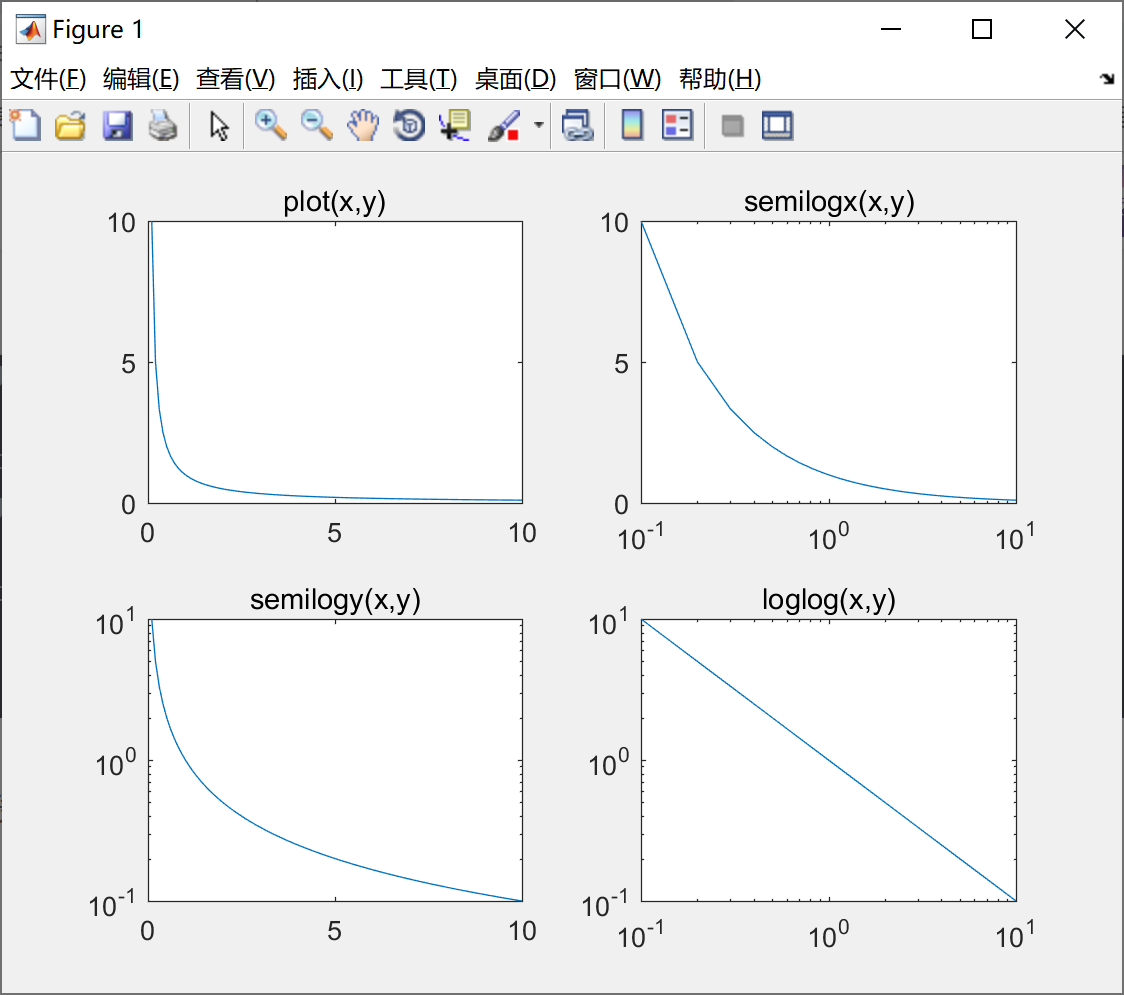
对数坐标图:我们看一下例子就可以。
在一个窗口绘制四种坐标图,代码如下所示:
x = 0 : 0.1 : 10 ;
y = 1./x ;
subplot(2,2,1) ;
plot(x,y) ;
title('plot(x,y)') ;
subplot(2,2,2) ;
semilogx(x,y) ;
title('semilogx(x,y)') ;
subplot(2,2,3) ;
semilogy(x,y) ;
title('semilogy(x,y)') ;
subplot(2,2,4) ;
loglog(x,y) ;
title('loglog(x,y)') ;绘制的图形入戏所示:
4- polar(theata,rho,选项)函数的基本用法
polar(theata,rho,选项)绘制极坐标图,theta表示极角,rho代表极径,选项与plot相同。
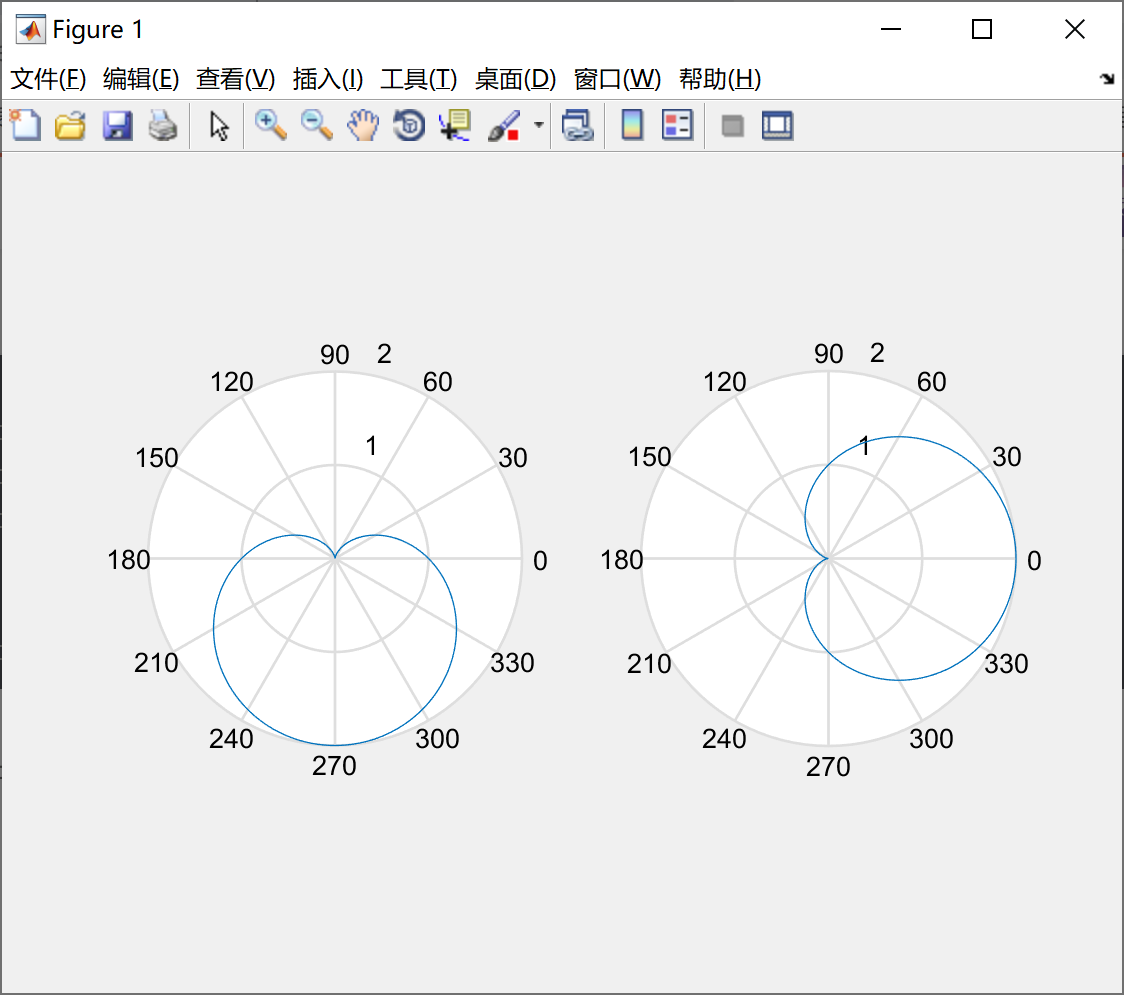
我们看一下例子2,通过极角和极径绘制极坐标图形,代码如下所示:
t = 0 : pi/100 : 2*pi ;
r = 1 - sin(t) ;
subplot(1,2,1) ;
polar(t,r) ;
subplot(1,2,2) ;
t1 = t - pi/2 ;
r1 = 1 - sin(t1) ;
polar(t,r1) ;绘制的图形如下所示:
5-bar(y,style)函数的基本用法
下面开始学习绘制统计图。
条形图的绘制:可以使用bar(y,style)函数绘制条形图,其中y是参数数据,style是分组排列模式,有簇状模式grouped和堆积模式stacked两种形式。
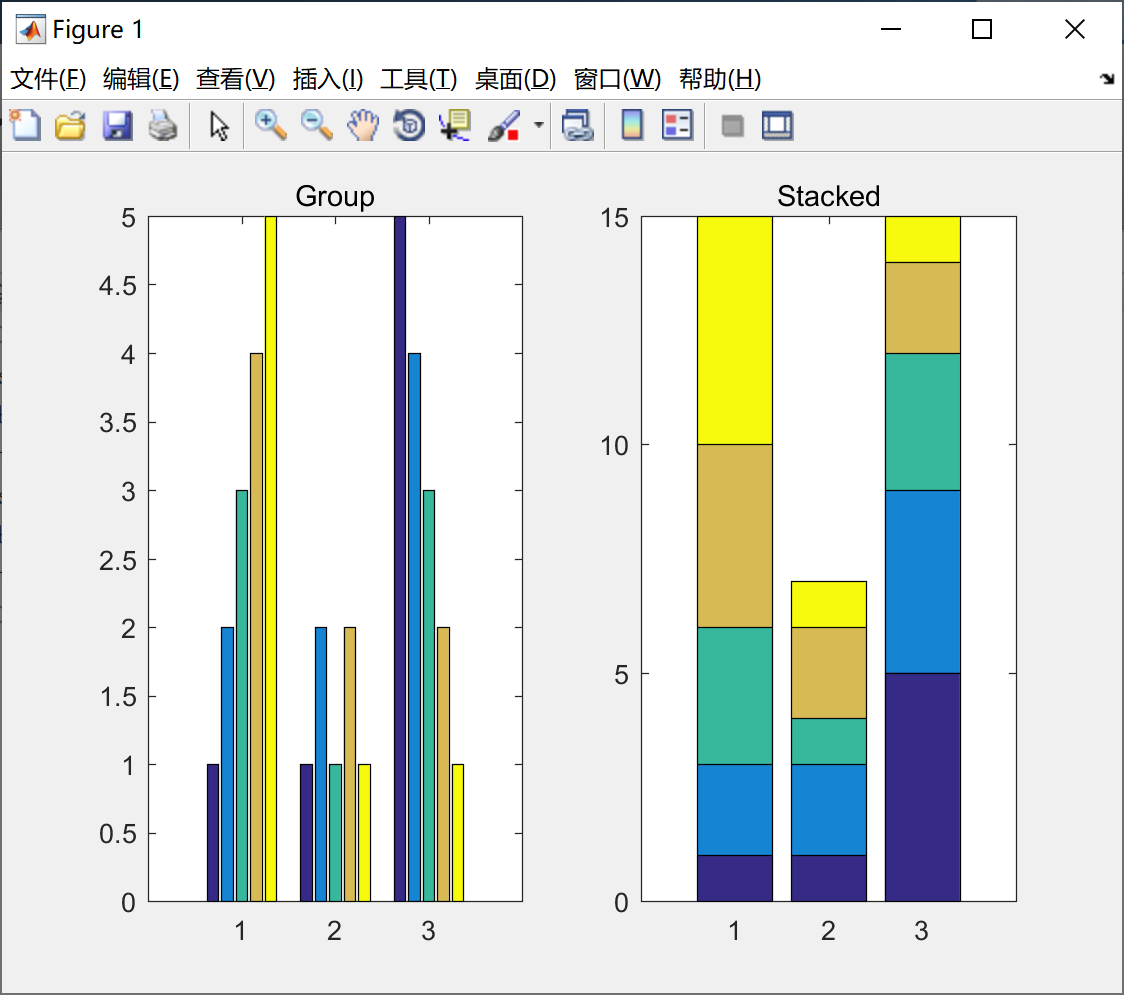
我们可以看一下例子3的绘制分组条形图,代码如下所示:
y = [1,2,3,4,5; 1,2,1,2,1; 5,4,3,2,1] ;
subplot(1,2,1) ;
bar(y) ;
title('Group') ;
subplot(1,2,2) ;
bar(y, 'stacked') ;
title('Stacked') ;
绘制的图形如下所示:
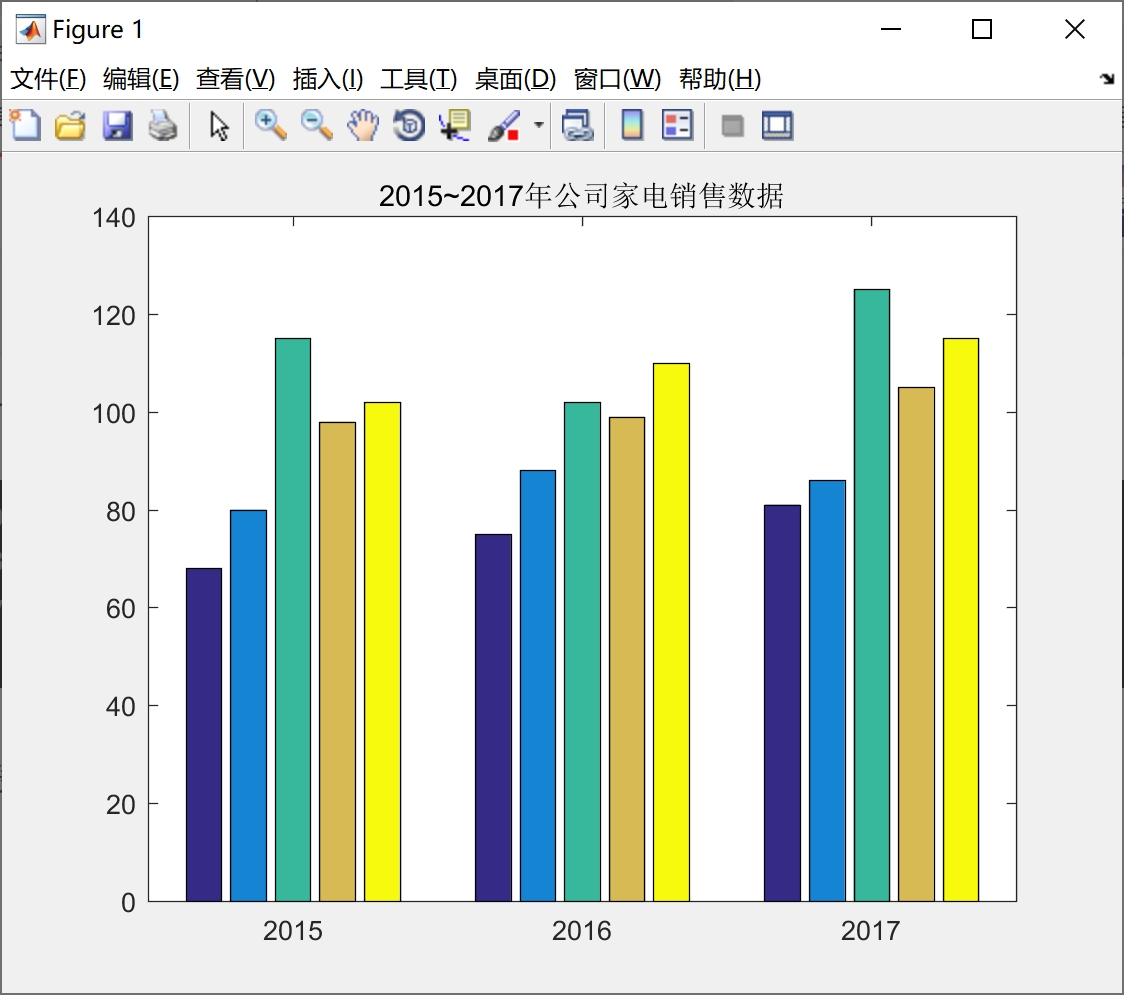
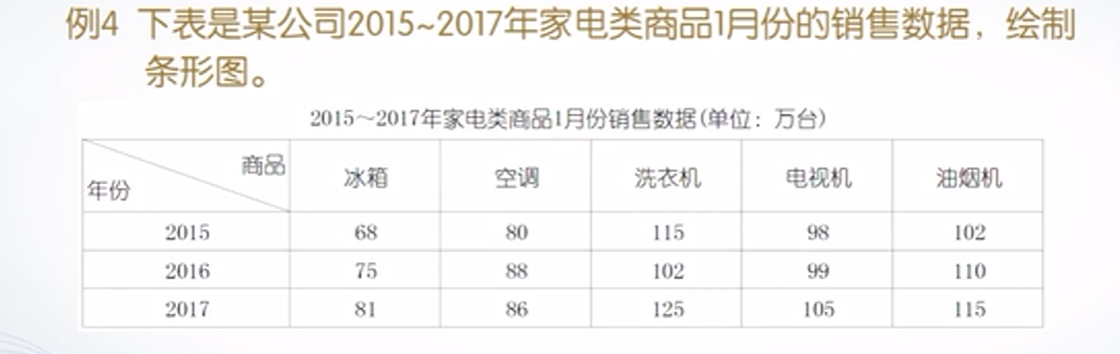
我们再看一下上面的例子4,绘制条形图,代码如下所示:
x = [2015, 2016, 2017] ;
y = [68,80,115,98,102; 75,88,102,99,110; 81,86,125,105,115] ;
bar(x,y) ;
title('2015~2017年公司家电销售数据') ;绘制的图形如下所示:
6-hist(y,x)函数和rose(theta,x)函数的基本用法
我们学习使用hist函数绘制直角坐标下的直方图和rose函数绘制极坐标下的直方图
hist(y,x)函数,y表示要统计的数据,x是指定的区间划分方式。
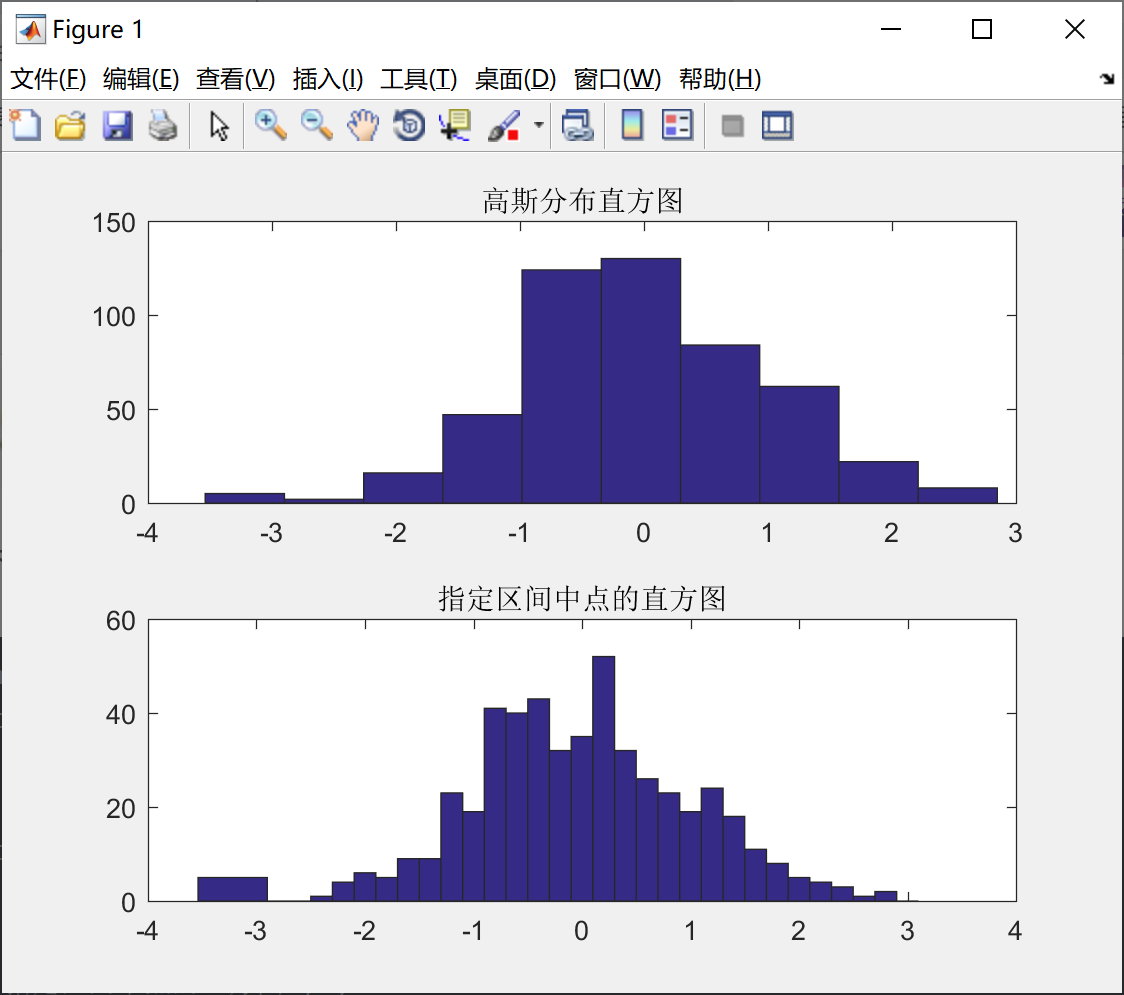
我们看一下例子5,绘制服从高斯分布的直方图,代码如下所示:
y = randn(500, 1) ;
subplot(2,1,1) ;
hist(y) ;
title('高斯分布直方图') ;
subplot(2,1,2) ;
x = -3:0.2:3 ;
hist(y,x) ;
title('指定区间中点的直方图') ;绘制的直方图如下所示:
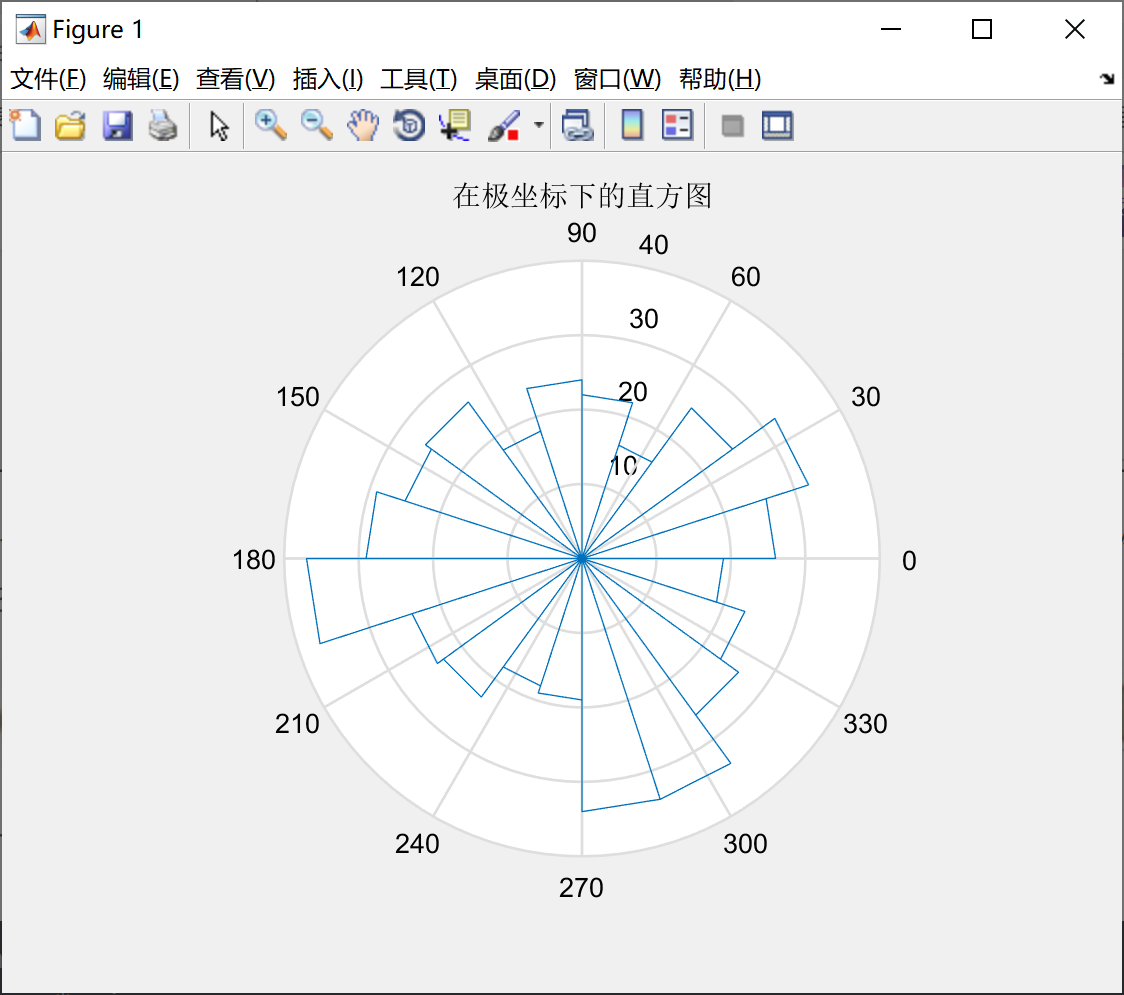
使用rose(theta,x)函数用于绘制极坐标系下的直方图。参数theta用于确定每一区间和原点的角度,选项x用于指定区间的划分方式。
我们看一下例子6,绘制高斯分布在极坐标下的直方图,代码如下:
y = randn(500,1) ;
theta = y * pi ;
rose(theta) ;
title('在极坐标下的直方图') ;
7-pie(x,explode)函数和area()函数的用法
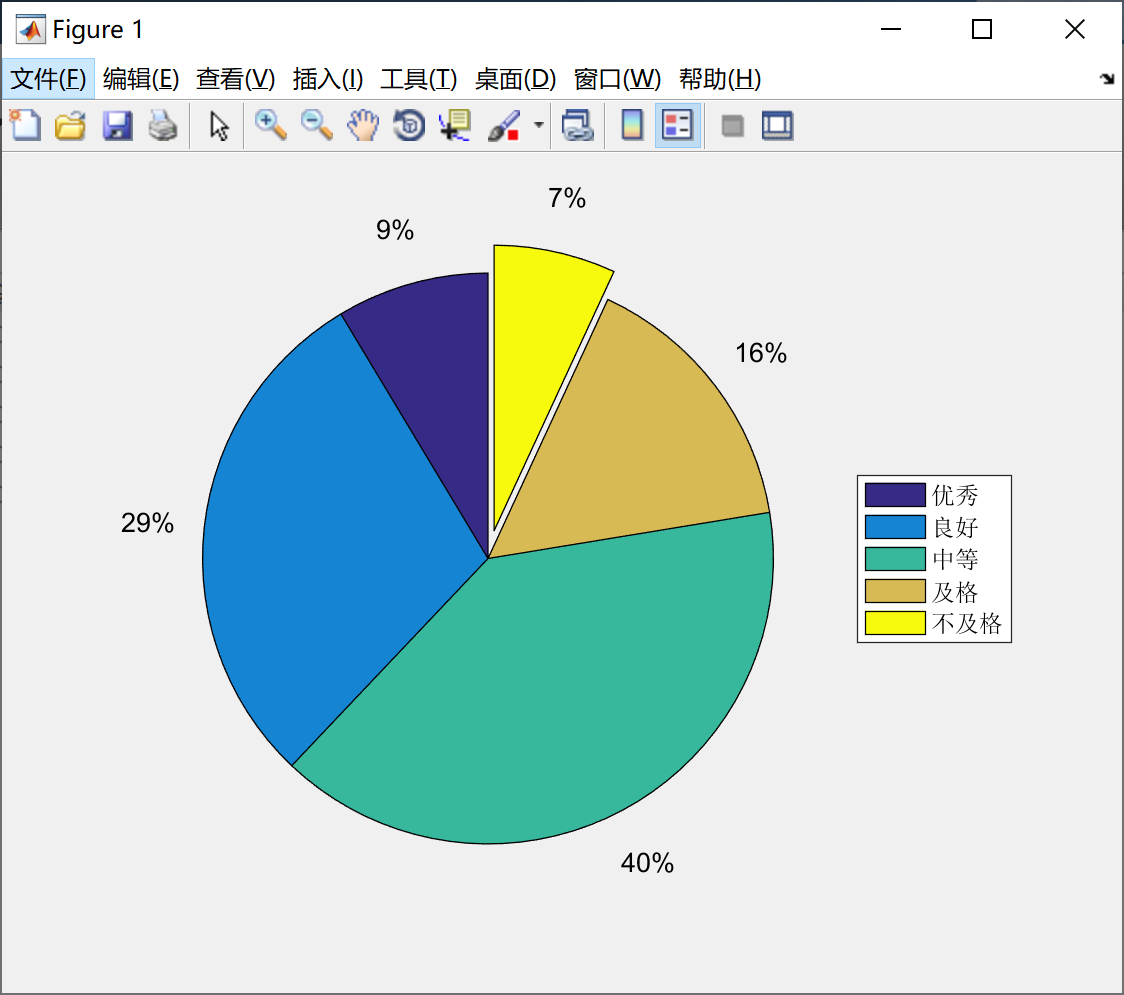
pie(x,explode)用于绘制扇形图,其中参数x存储待统计的数据,选项explode控制图块的显示模式。
我们看一下例子7,代码如下所示:
score = [5,17,23,9,4] ;
ex = [0,0,0,0,1] ; %存储图形显示控制符,将最后一个移出来
pie(score, ex) ;
legend('优秀','良好','中等','及格','不及格','location','eastoutside') ;绘制的扇形图如下所示:
8-scatter()函数、stairs()函数、stem()函数的应用
三个类似,这边只介绍scatter(x,y,选项,‘field’)函数,其中x,y用于定位数据点,选项用于指定线形,颜色,数据点标记。
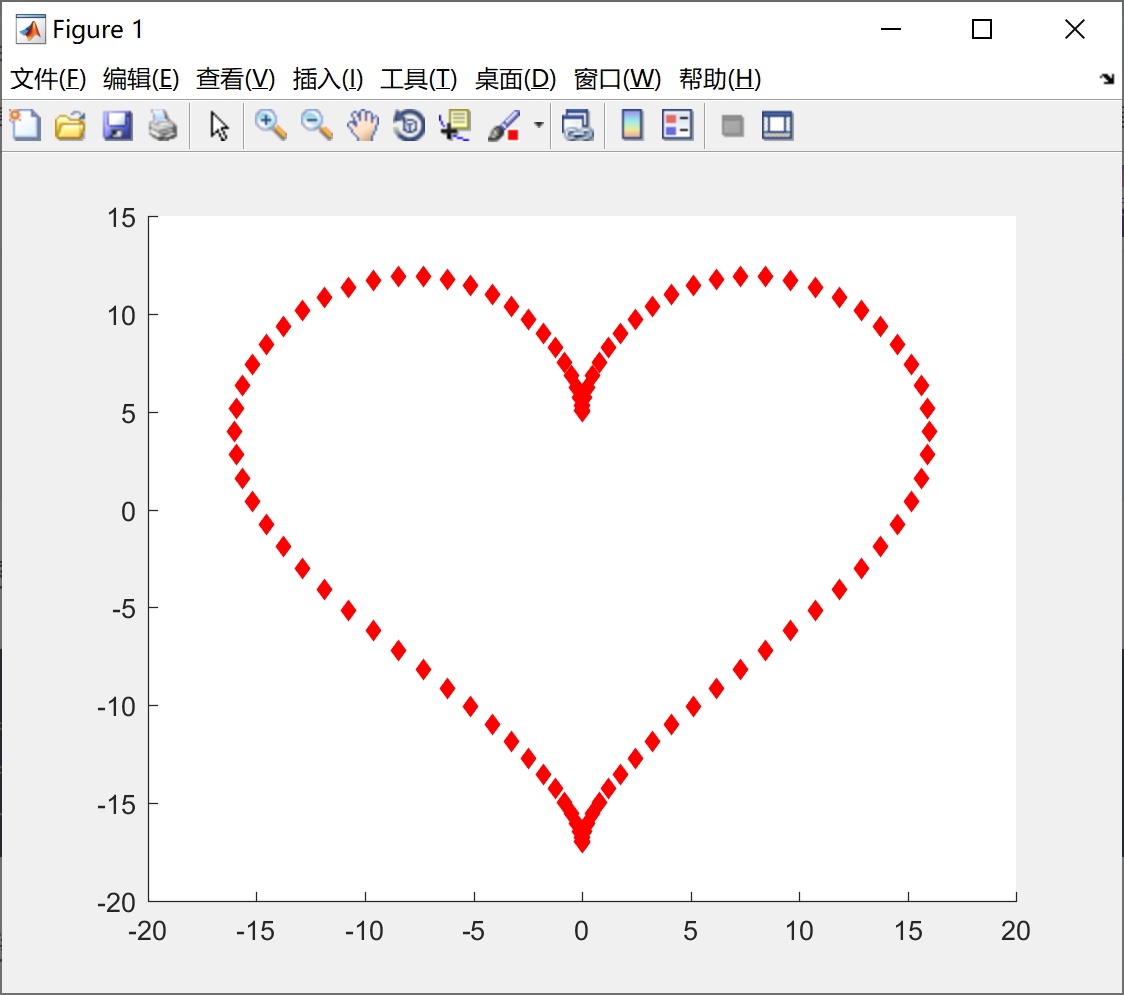
scattter()函数用于画散点图,我门看一下例子8,代码如下所示:
t = 0 : pi/50 : 2*pi ;
x = 16*sin(t).^3 ;
y = 13*cos(t) - 5*cos(2*t)- 2*cos(3*t) - cos(4*t) ;
scatter(x,y,'rd','filled') ;绘制的心形图形如下所示:
9-compass()函数、feather()函数、quiver()函数的应用
compass()函数用于绘制罗盘图,feather()函数用于绘制羽毛图,quiver()函数用于绘制箭头图,用法和plot()函数类似。
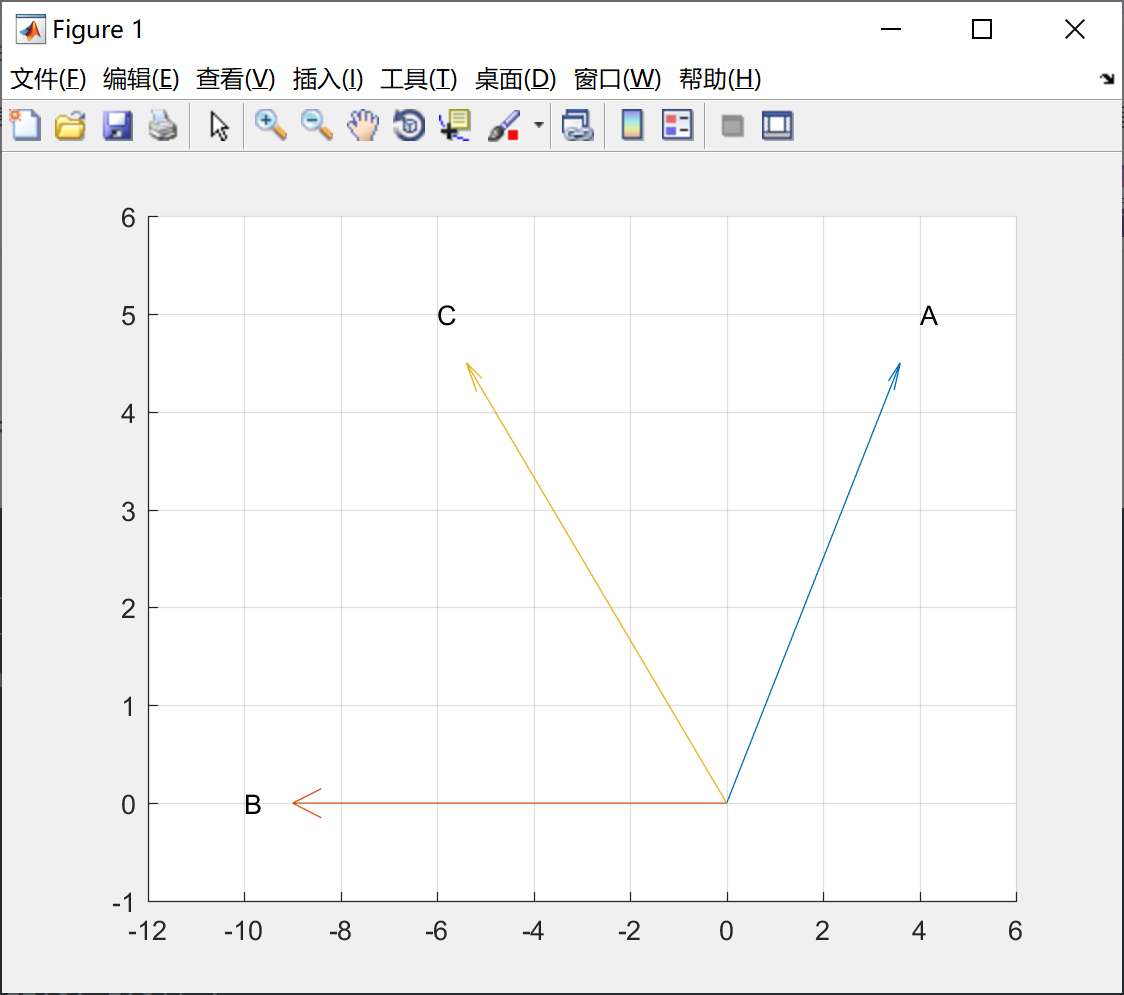
例如:quiver(x,y,u,v)函数,其中(x,y)为矢量起点,(u,v)为矢量终点。
我们看一下上面的例子9,代码如下所示:
A = [4,5] ;
B = [-10, 0] ;
C = A + B ;
hold on ;
quiver(0,0,A(1),A(2)) ;
quiver(0,0,B(1),B(2)) ;
quiver(0,0,C(1),C(2)) ;
text(A(1),A(2),'A') ;
text(B(1),B(2),'B') ;
text(C(1),C(2),'C') ;
axis([-12,6,-1,6]) ;
grid on ;绘制的矢量图形如下所示:
最后
以上就是感动山水最近收集整理的关于备战数学建模3-MATLAB绘制各种二维图形的全部内容,更多相关备战数学建模3-MATLAB绘制各种二维图形内容请搜索靠谱客的其他文章。























发表评论 取消回复