matlab波特图怎么查数据,波特图怎么分析_波特图分析方法

描述

波特图的定义

波特图是线性非时变系统的传递函数对频率的半对数坐标图，其横轴是频率，纵轴以对数尺度(logscale)表示，利用波特图可以看出系统的频率响应。波特图一般是由二张图组合而成，一张幅频图表示频率响应增益的分贝值对频率的变化，另一张相频图则是频率响应的相位对频率的变化。

波特图可以用电脑软件(如MATLAB)或仪器绘制，也可以自行绘制。利用波特图可以看出在不同频率下，系统增益的大小及相位，也可以看出大小及相位随频率变化的趋势。

波特图的图形和系统的增益，极点、零点的个数及位置有关，只要知道相关的资料，配合简单的计算就可以画出近似的波特图，这是使用波特图的好处。

波特图(Bode Plots)

波特图(Bode Plots)可用来确认回路的稳定性，回路的增益(Loop Gain，单位：dB)是频率(Frequency)的函数(图5：典型的波特图)。 回路增益可以用网络分析仪(Network Analyzer)测量。 网络分析仪向反馈回路(Feedback Path)注入低电平的正弦波(Sine Wave)，随着直流电压(DC)的不断升高， 这些正弦波信号完成扫频，直到增益下降到0dB。然后测量增益的响应(Gain Response)。

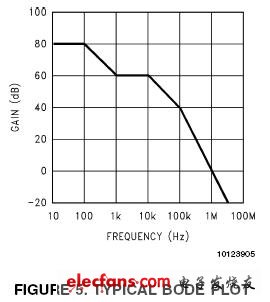
图5

波特图是很方便的工具，它包含判断闭环系统(Closed-loop System)稳定性的所有必要信息。 包括下面几个关键参数：环路增益(Loop Gain)，相位裕度(Phase Margin)和零点(Zeros)、极点(Poles)。

波特图分析

用包含三个极点和一个零点的波特图(图11：波特图)来分析增益和相位裕度。

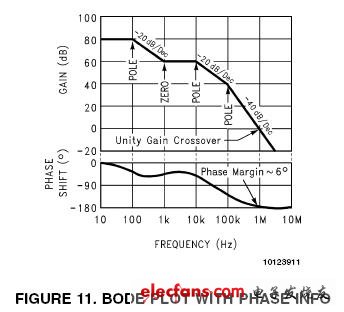
图11

假设直流增益(DC gain)为80dB，第一个极点(pole)发生在100Hz处。在此频率，增益曲线的斜度变为－20dB/十倍频程。1kHz处的零点使斜度变为0dB/十倍频程，到10kHz处斜度又变成－20dB/十倍频程。在100kHz处的第三个也是最后一个极点将斜度最终变为－40dB/十倍频程。

图11中可看到单位增益点(Unity Gain Crossover，0dB)的交点频率(Crossover Frequency)是1MHz。0dB频率有时也称为回路带宽(Loop Bandwidth)。

相位偏移图表示了零、极点的不同分布对反馈信号的影响。为了产生这个图，就要根据分布的零点、极点计算相移的总和。在任意频率(f)上的极点相移，可以通过下式计算获得： 极点相移 ＝ -arctan(f/fp) (6)

在任意频率(f)上的零点相移，可以通过下式计算获得： 零点相移 ＝ -arctan(f/fz) (7)

此回路稳定吗？为了回答这个问题，我们根本无需复杂的计算，只需要知道0dB时的相移(此例中是1MHz)。

前两个极点和第一个零点分布使相位从-180°变到+90°，最终导致网络相位转变到-90°。最后一个极点在十倍频程中出现了0dB点。代入零点相移公式，可以计算出该极点产生了－84°的相移(在1MHz时)。加上原来的-90°相移，全部的相移是-174°(也就是说相位裕度是6°)。由此得出结论，该回路不能保持稳定，可能会引起振荡。

#p#

波特图应用

#e#

波特图应用

现在以一简单的低通滤波器来窥探下波特图的魅力。

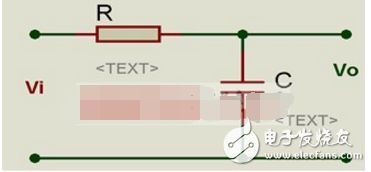
传递函数

我们将该点叫做频率转折点，在频率较低的范围内，增益大约为1，在频率较高的范围内，系统增益以-20dB/10倍频的速度下降。在滤波器设计中，也就是我们常听到的3dB带宽的截止频率。低通滤波器的波特图频率响应部分如下所示：

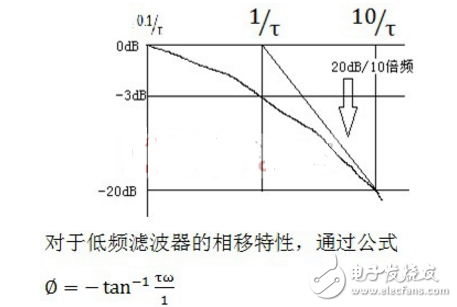
由于正切函数是非线性的，描述其特性比较难搞，其实我们可以依据我们拥有的基础数学知识来近似描述该函数：

位为0°、45°和90°。在波特图的相频图中画出相应曲线，如下图所示：

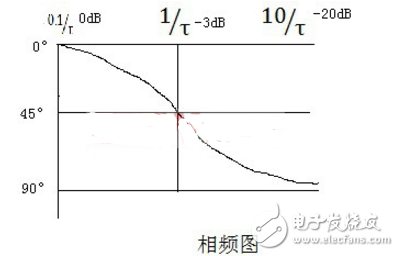
以上以一简单的一阶低通滤波器作为例子进行系统的波特图分析和画制，在实际的工程中，常常会因为采用多个电容和电阻构成了更加负责的系统，其实原理分析都是如此，只不过在分析过程中，找出关键位置的频率点，就能掌握系统传递函数的纲要，达到高屋建瓴的效果。

在多极点和零点传递函数中，使分母为零的频率点叫极点，使分子频率为零的频率点叫零点，极点可以使增益曲线下降，零点使增益曲线上升。在多极点和零点的系统中，只要找到各个极点和零点，找出其特性，将各个增益曲线叠加即可实现系统的极零分析，这个定理可以帮助大家在画多极点和零点的传递函数有个直观的印象。

打开APP阅读更多精彩内容

点击阅读全文