概述
1 传递函数模型的建立：tf()
1.1 格式：G=tf(num,den)，num和den分别代表分子分母的零极点
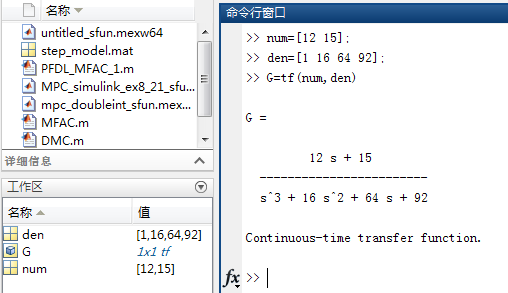
输出为连续时间传递函数模型
注：工作区的模型G对应“1*1 tf”表示G为单输入单输出SISO系统
1.2 阶跃响应测试：step（G）
格式：step（G）
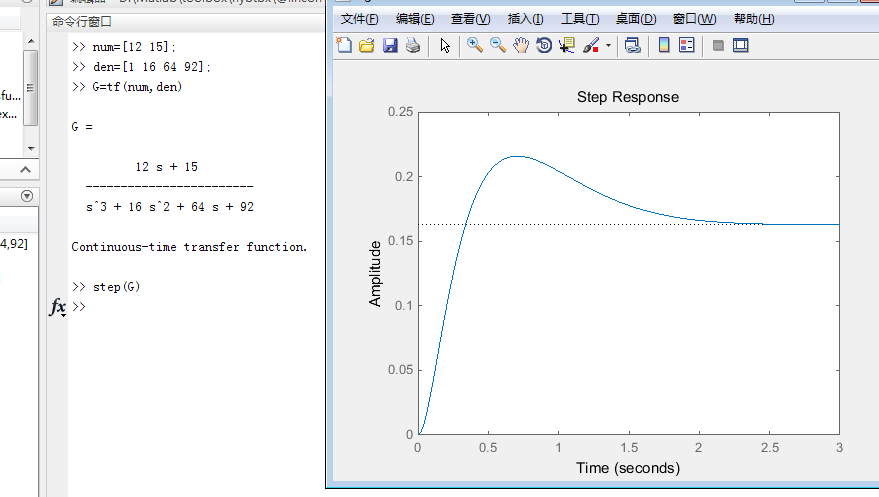
还可在step（）里增加仿真时间
eg：step（G,10）
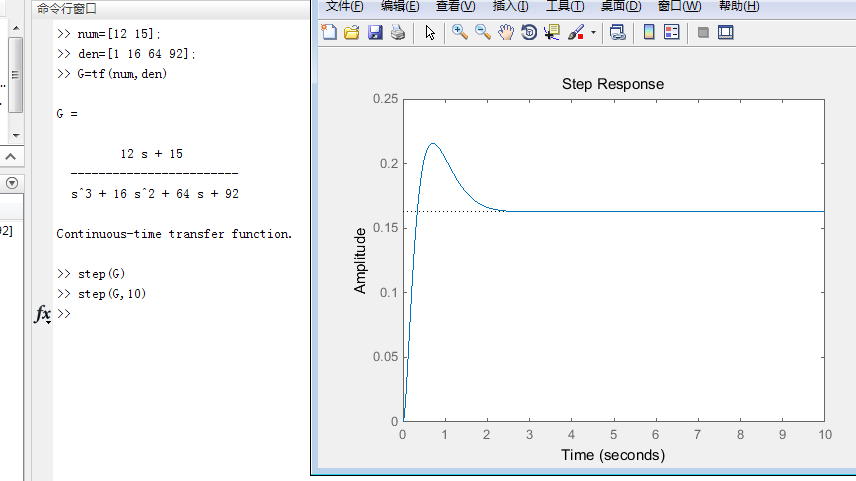
1.3 用分式的形式来表示传递函数
格式：s=tf(‘s’)，s来代替拉式算子
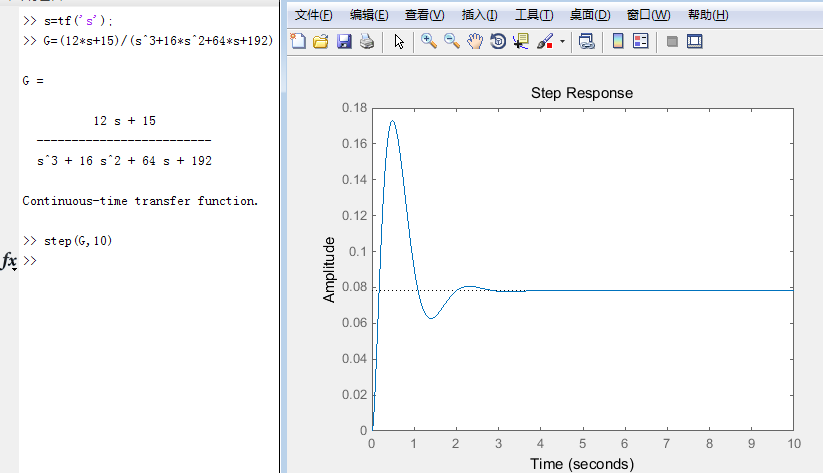
1.4 输入一个带时延的传递函数
格式：G=tf(num,den,‘ioDelay’,time)
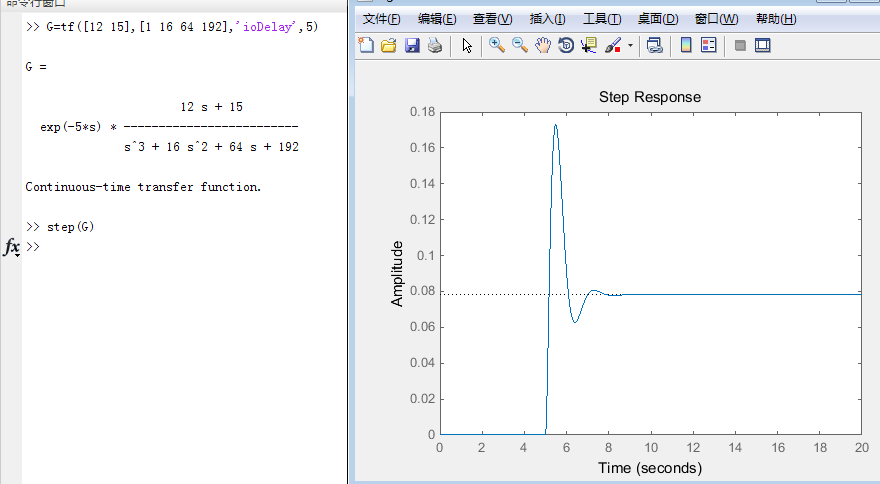
注：拉式算子’s’同样适用该情况
2 零极点模型的建立：zpk()
2.1 格式：G=zpk(z,p,k) ，零点向量z、极点向量p和输入增益k
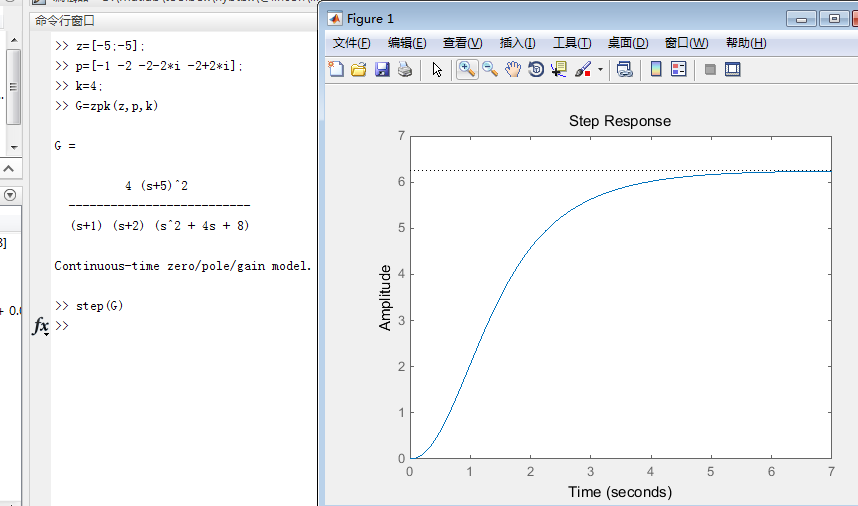
注：拉式算子’s’同样适用于zpk()
2.2 求零极点向量和增益值：
格式：[z p k] = zpkdata(G,‘v’)，G模型，‘v’表向量形式
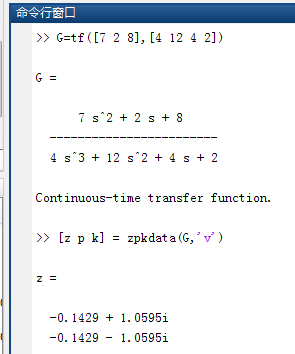
可知系统G有两个开环零点，3个开环极点，增益为1.75
若去掉‘v’，格式：[z p k] = zpkdata(G)
2.3 由传递函数模型得到零极点模型
在2.2中，根据传递函数求得的零极点向量z,p和增益k，可以由G1=zpk(z,p,k)求得传递函数模型G对应的零极点模型G1
2.4 绘制系统零极点分布
格式：pzmap(G)
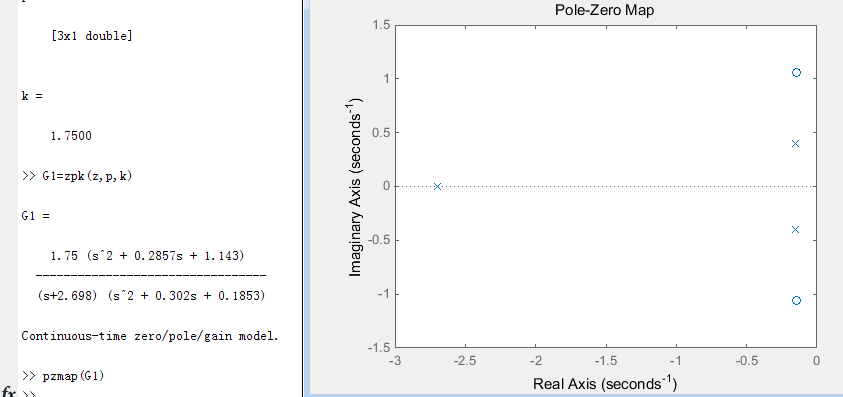
最后
以上就是精明大神为你收集整理的MATLAB实现传递函数模型、零极点模型和状态空间模型的建立与转换（1）的全部内容，希望文章能够帮你解决MATLAB实现传递函数模型、零极点模型和状态空间模型的建立与转换（1）所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复