matlab伯德图绘制_Bode Plots（伯德图）

Bode Plots(伯德图)

关于伯德图的一点回顾

所谓的频响特性(伯德图)指的是：

系统在正弦信号的激励下稳态响应随信号频率的变化情况。包含幅度随频率的响应、相位随频率的响应两个方面。

对于稳定系统

当输入为正弦信号的时候，输出一定是同频率的正弦信号，可以让s=jω。这种情况下拉式变化就变成了傅里叶变换。H(jω)就可以描述频响特性，。

对于不稳定的系统

对于不稳定的系统，存在右半平面的极点。它的收敛域就碰不到s平面的虚轴，也就是s=σ+jω中的σ≠0，也就没法变为傅里叶变换，没法用H(jω)描述频响特性。

但是我们强行让s=jω代表了什么？对于不稳定的系统，输入正弦信号，输出是发散的，那么哪来的幅频特性曲线(伯德图)？可以这么理解：取s=jω画出来的“幅值响应”，是频率为ω的正弦分量的“稳定分量”的频率特性。

至于发散的幅值，可以说：存在一个特殊的输入，使不稳定系统的输出不发散，我们要分析的是这个“稳态”和“特殊输入”两个要素反映的该不稳定系统的频率响应，也就是伯德图。

画伯德图的方法

幅值定义

对于单极点系统，幅值的计算如下：

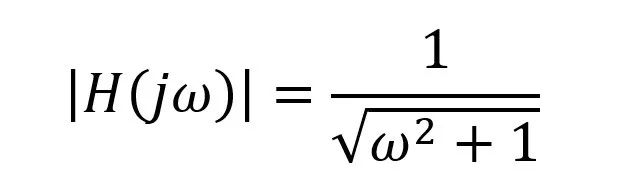
幅频特性曲线画法

角度(相位)定义

对于单极系统，相位

∠H(jω)=-arctanω

相频特性曲线画法

以单极点为例子

从0度到-90度的平滑过渡，通常徒手绘制，左右的边界大概2 decades。

如果需要更大的精度，有两个常用的近似画法：用于绘制一个极点(或零点)的分段线性角渐近线。假设极点位置在ωp处，两种方法的不同之处在于直线从0度到-90度的斜率。

方法1. 绘制从0.1wp到10wp的线性过渡折线。这种方法角度变化的频率范围延长到2 decades，并以非常小的总误差。然而，这个近似低估相位在wp的变化斜率。

方法2. 画一个从0.2wp到5wp的线性角过渡。该方法以较大的误差为代价来换取wp处的斜率准确度。

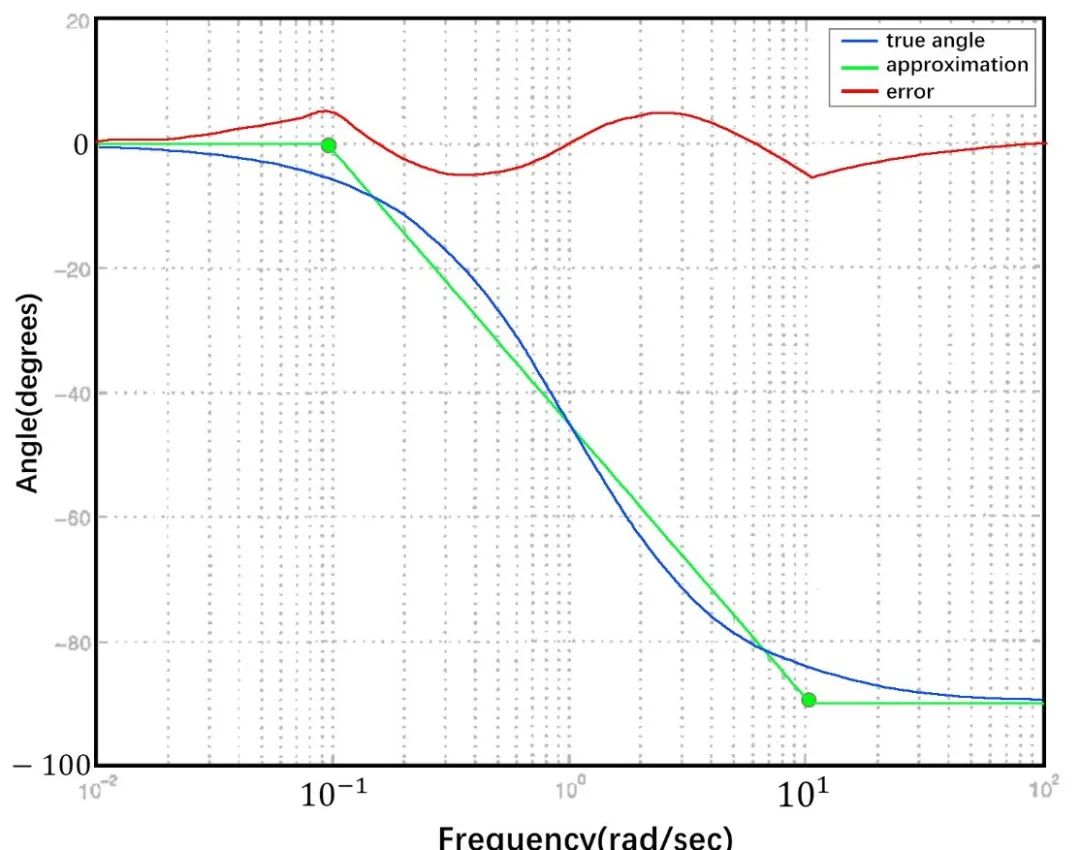
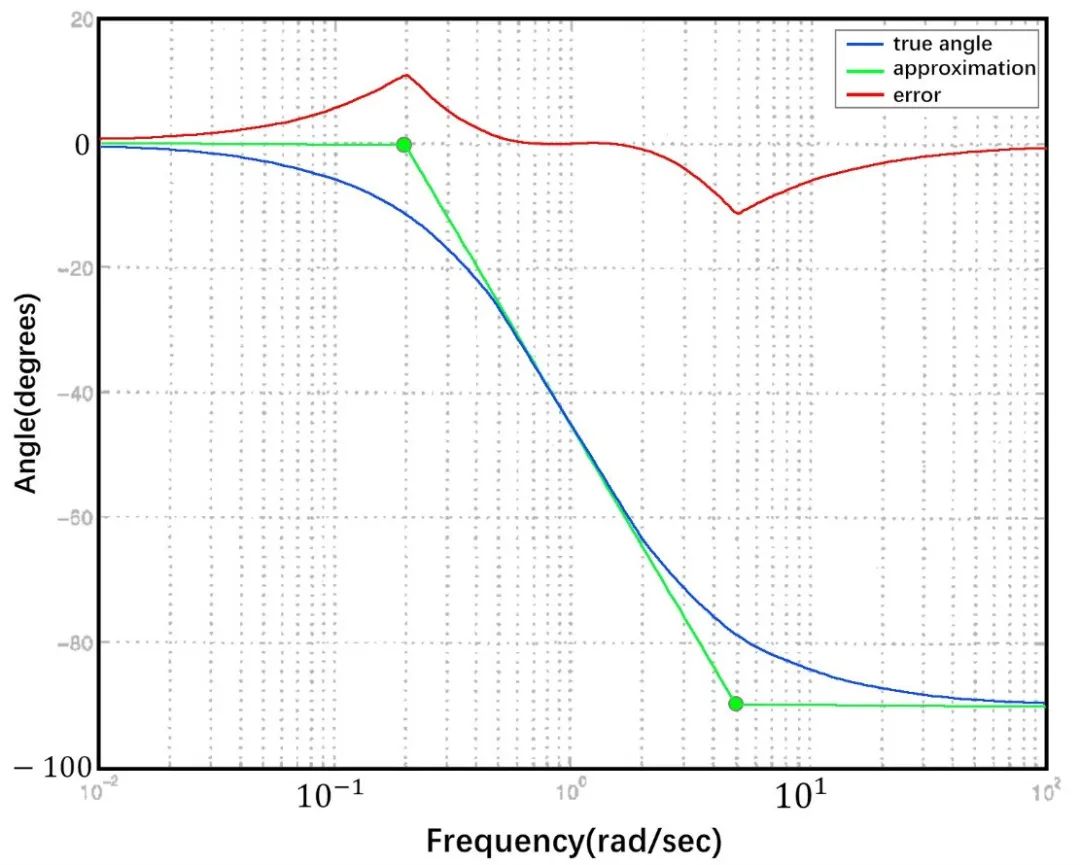
选择取决于应用的精确度，以及感兴趣的频率范围。

打些栗子，举些比方

每个例子会画出三维幅值图、零极点图、伯德图、阶跃响应。

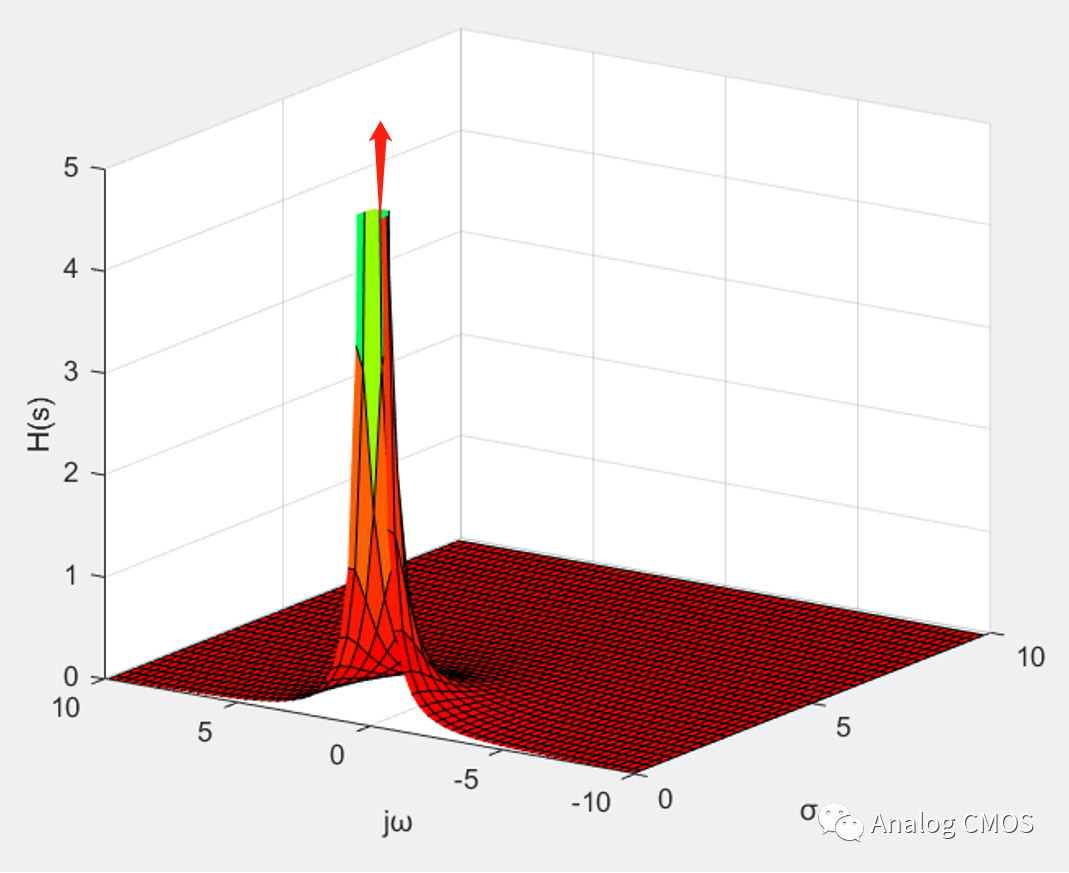
H(s)三维幅值坐标图↓↓

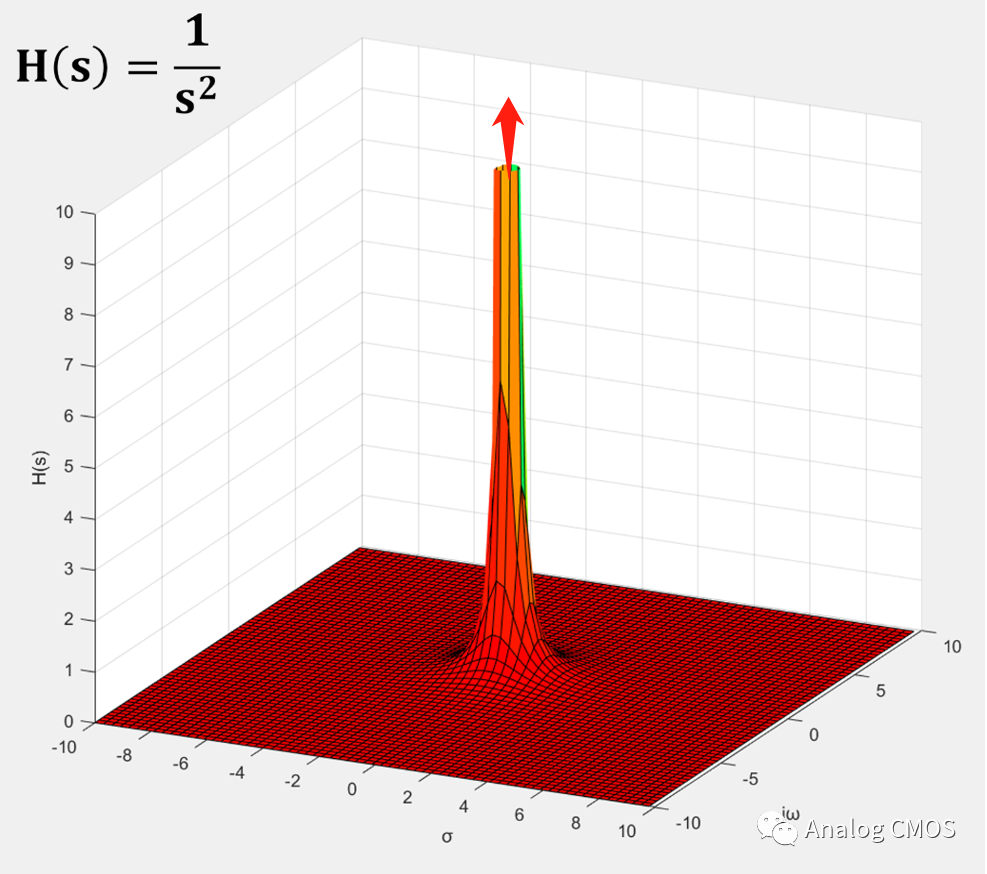
 s=jω时的剖面图↓↓

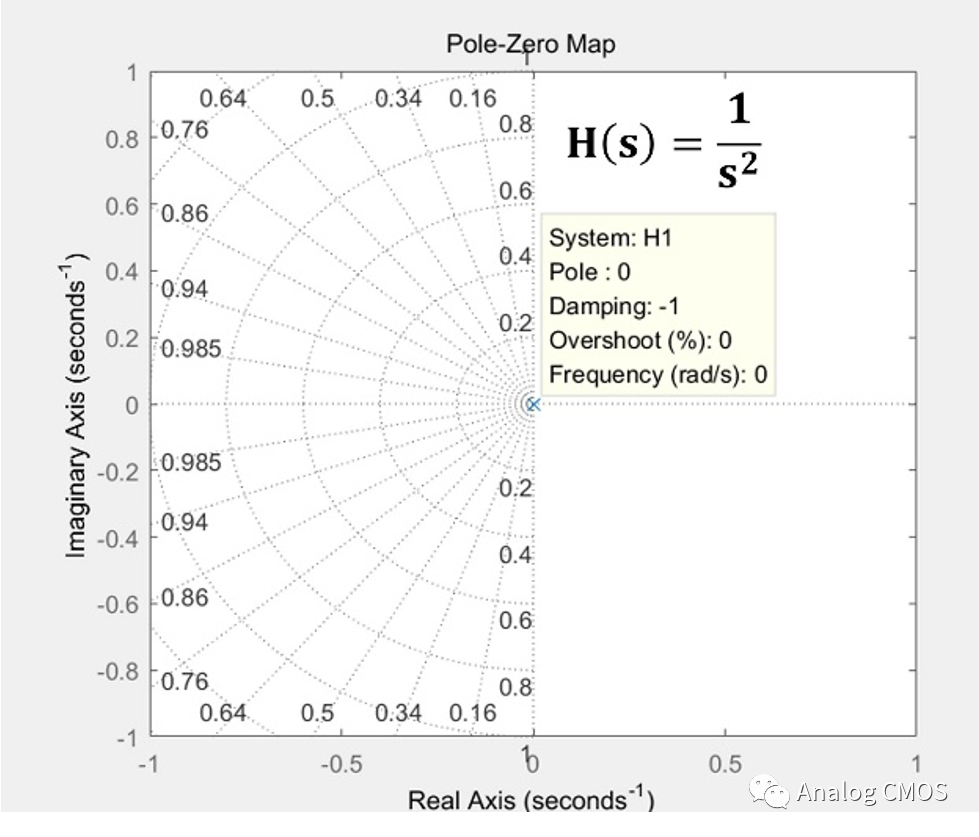
零极点图(俯视图)↓↓

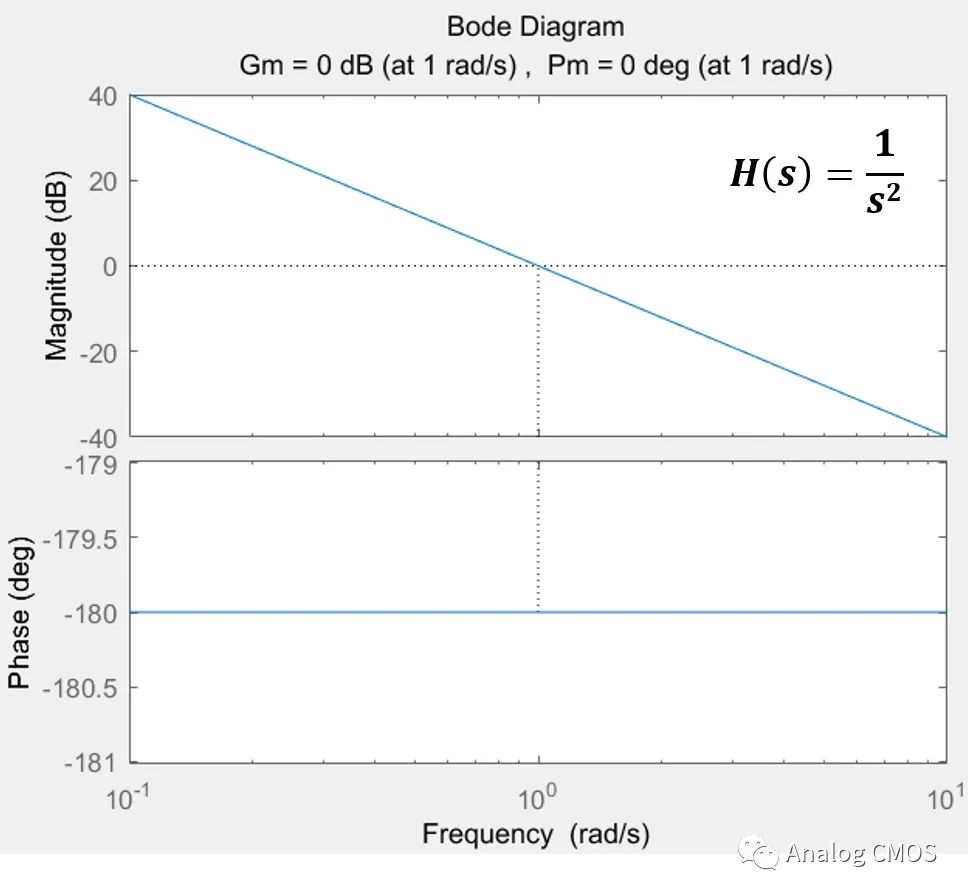
伯德图↓↓

阶跃响应↓↓

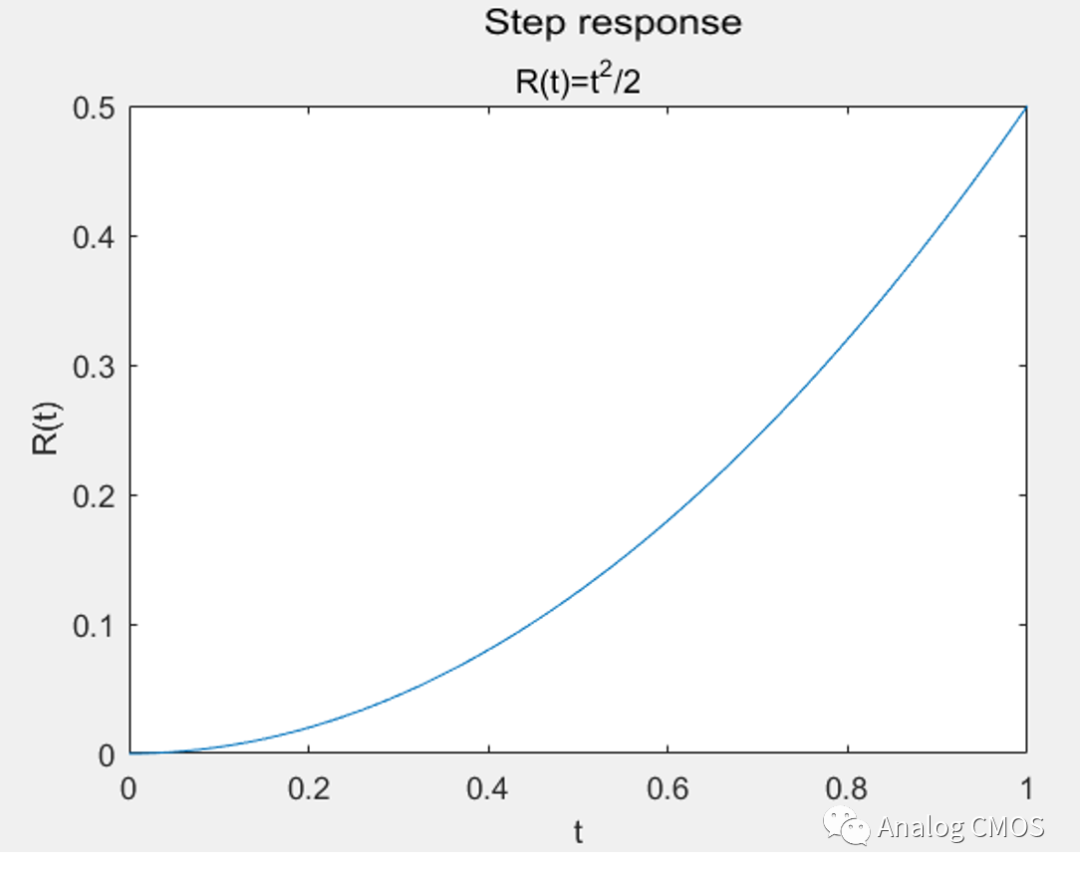
阶跃响应的计算

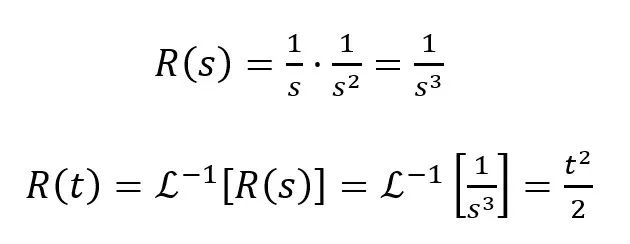
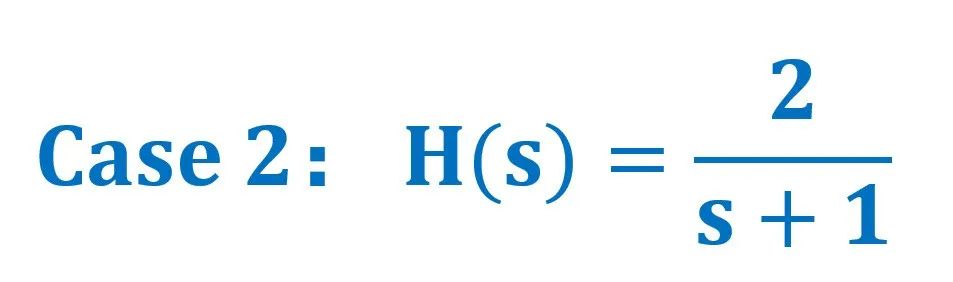
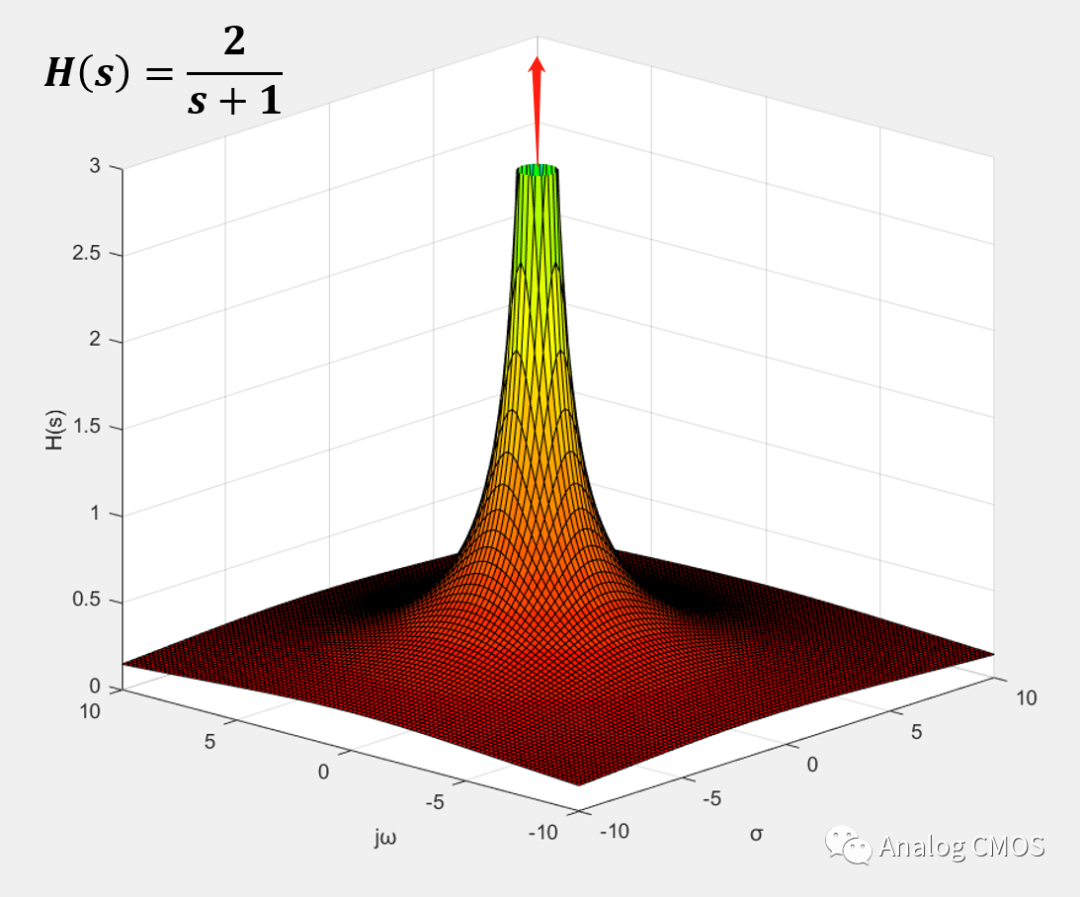
H(s)三维幅值坐标图↓↓

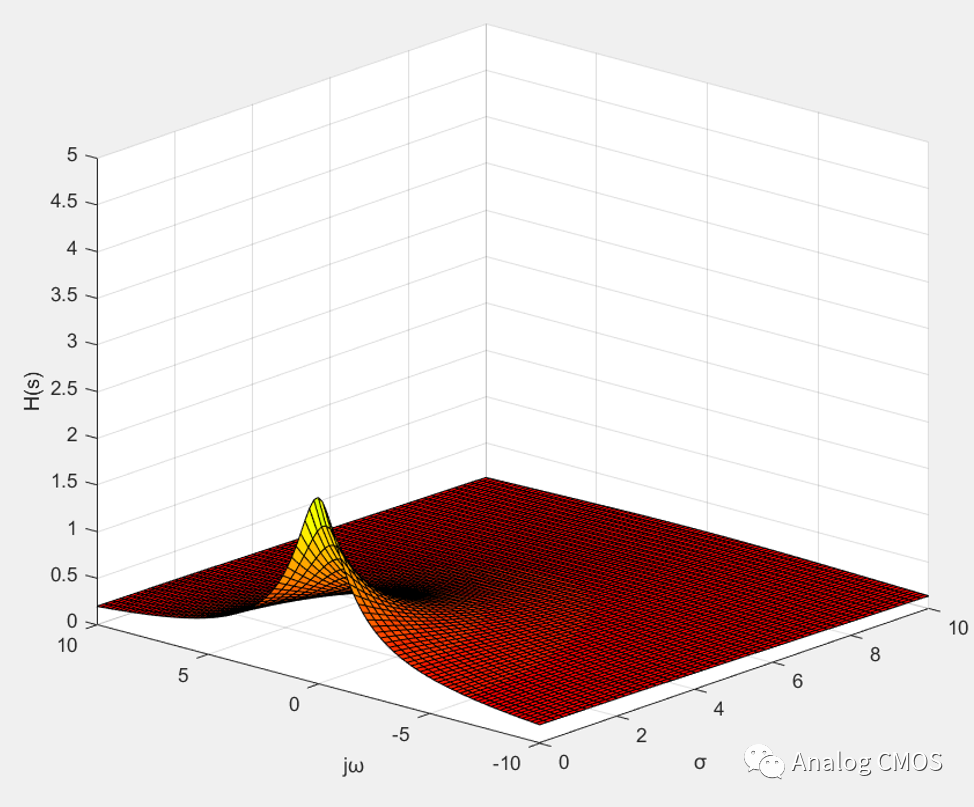
 s=jω时的剖面图↓↓

零极点图(俯视图)↓↓

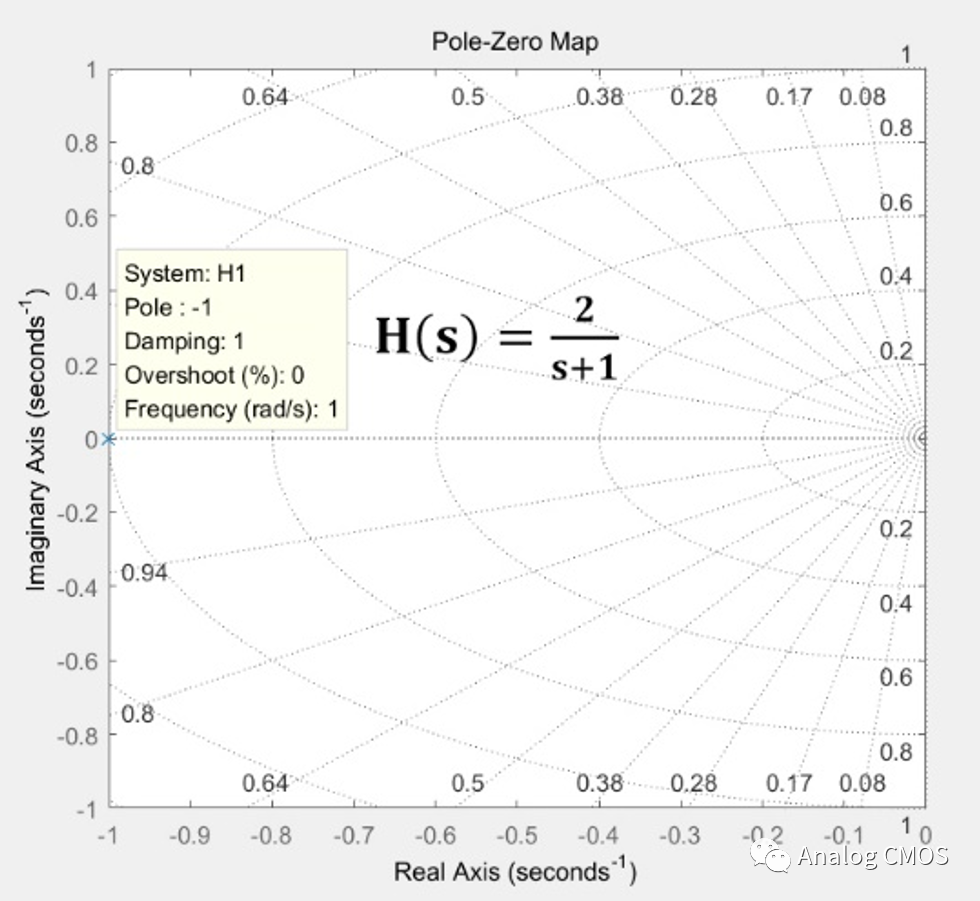
伯德图↓↓

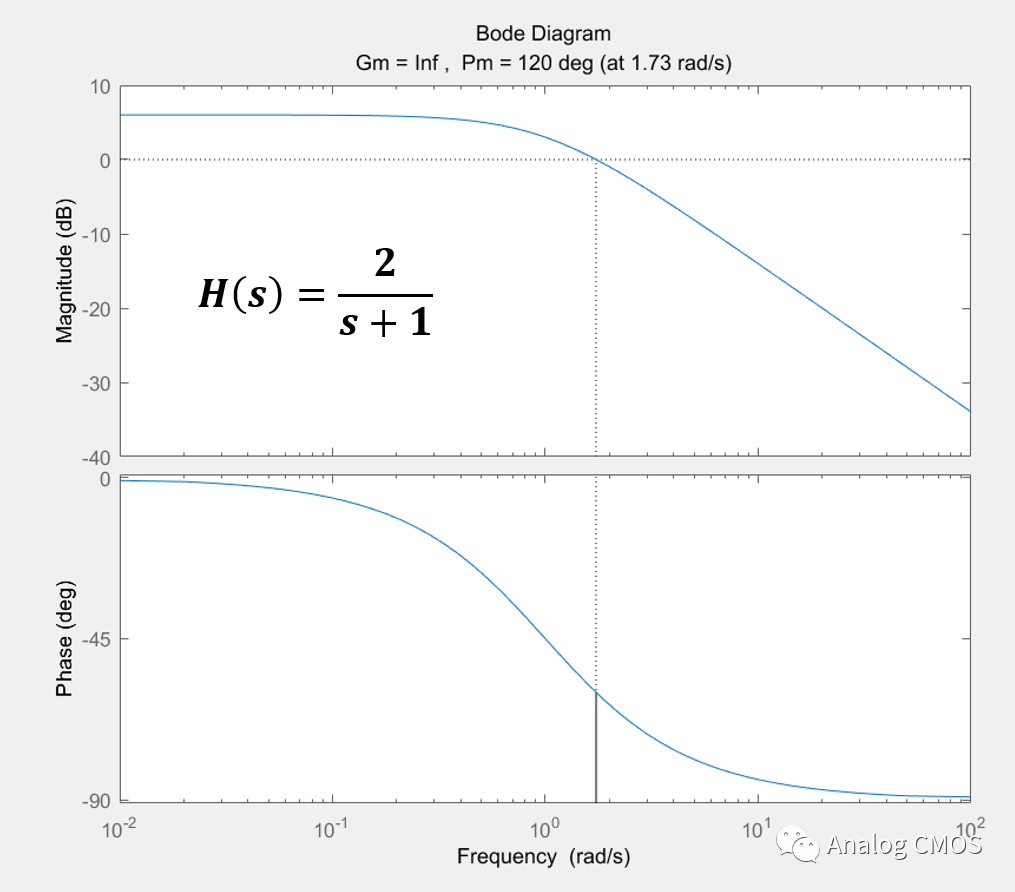
阶跃响应↓↓

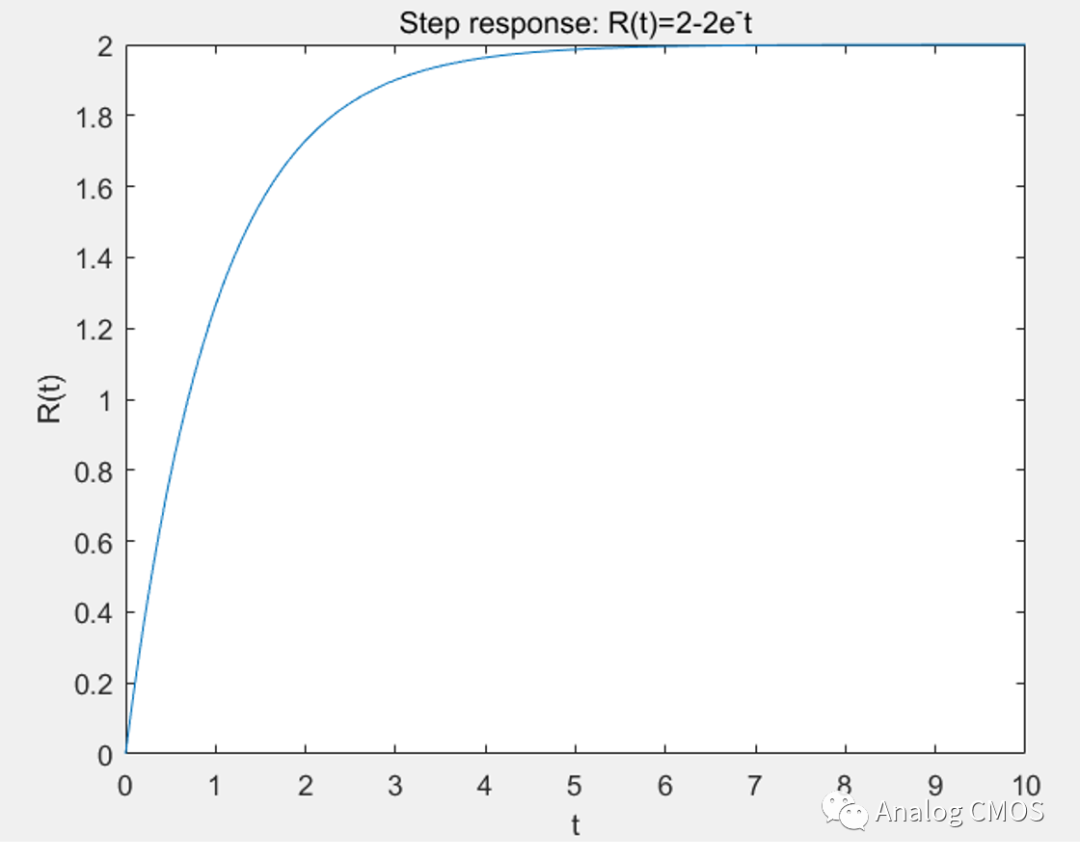
阶跃响应的计算↓

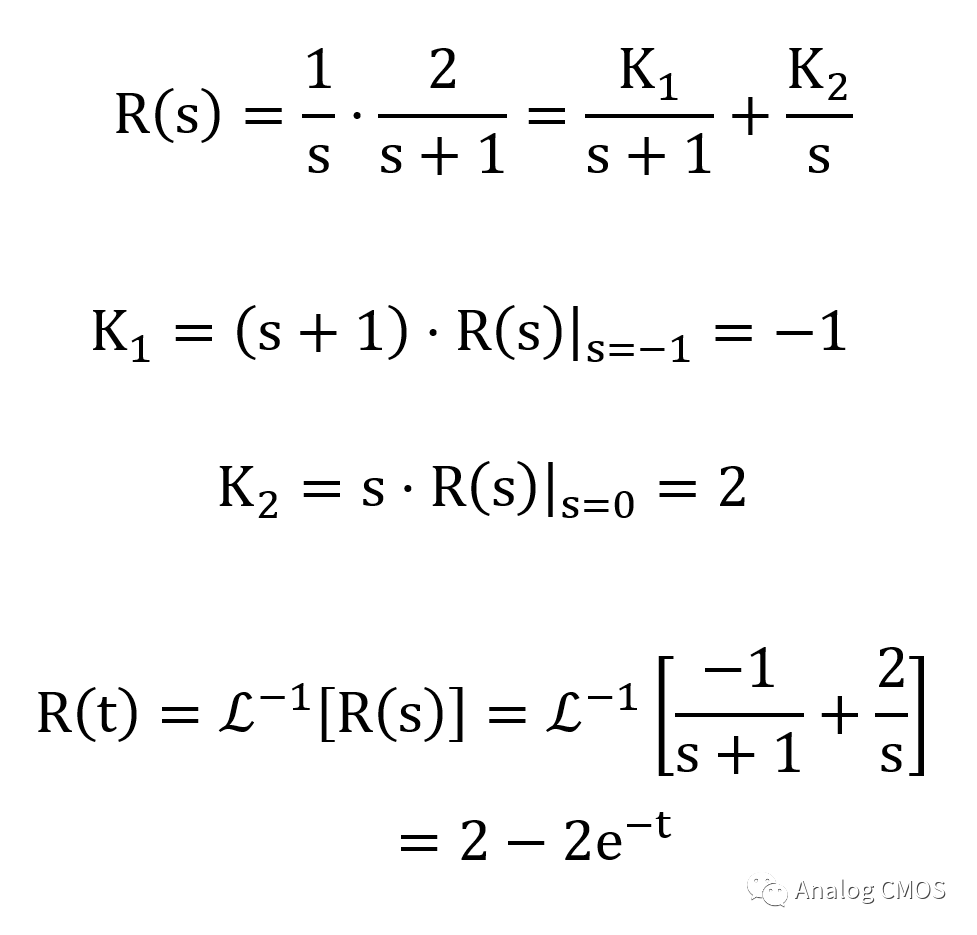
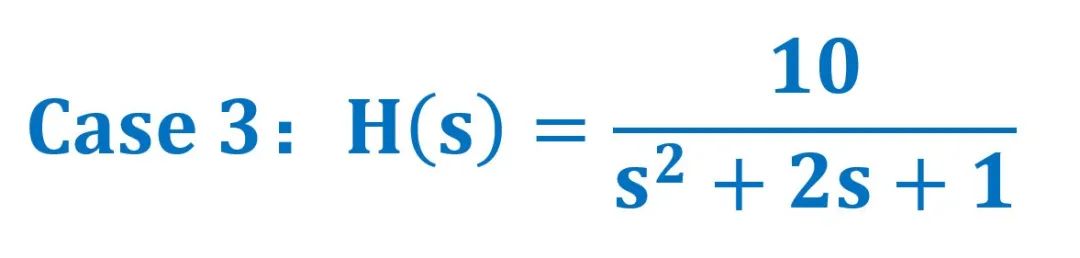
H(s)三维幅值坐标图↓↓

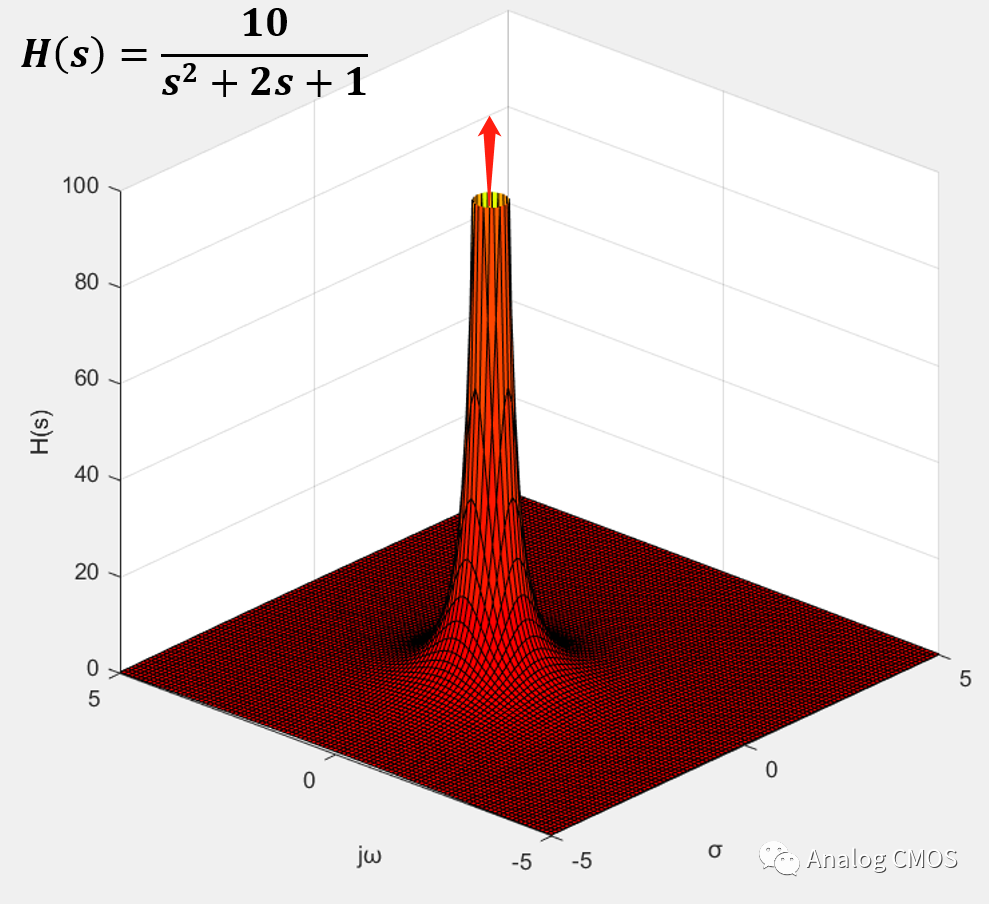
 s=jω时的剖面图↓↓

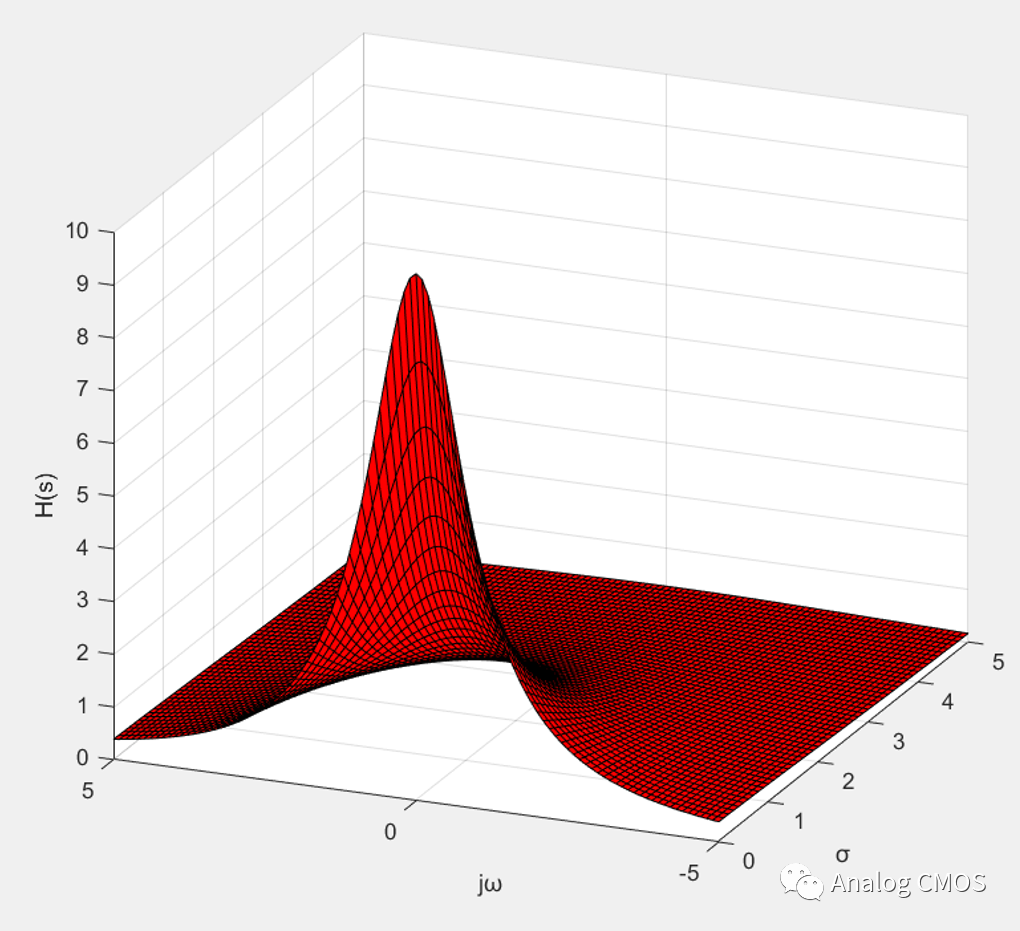
零极点图↓↓

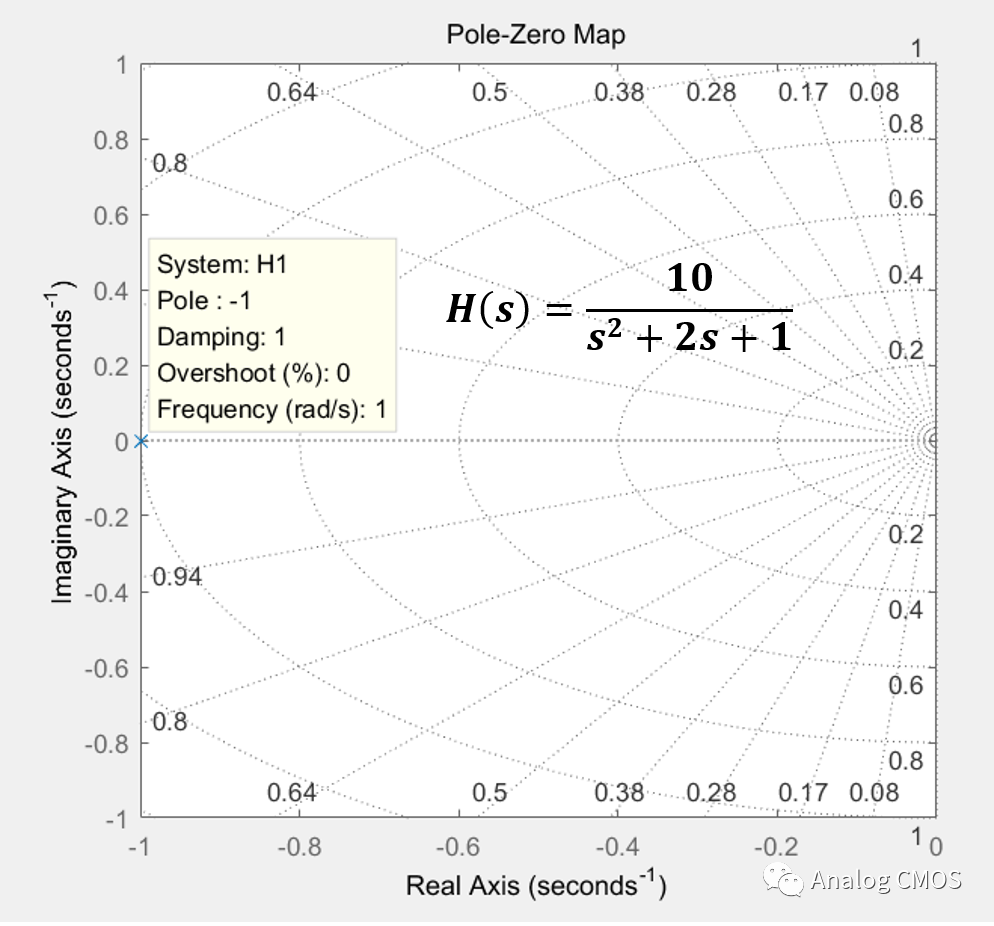
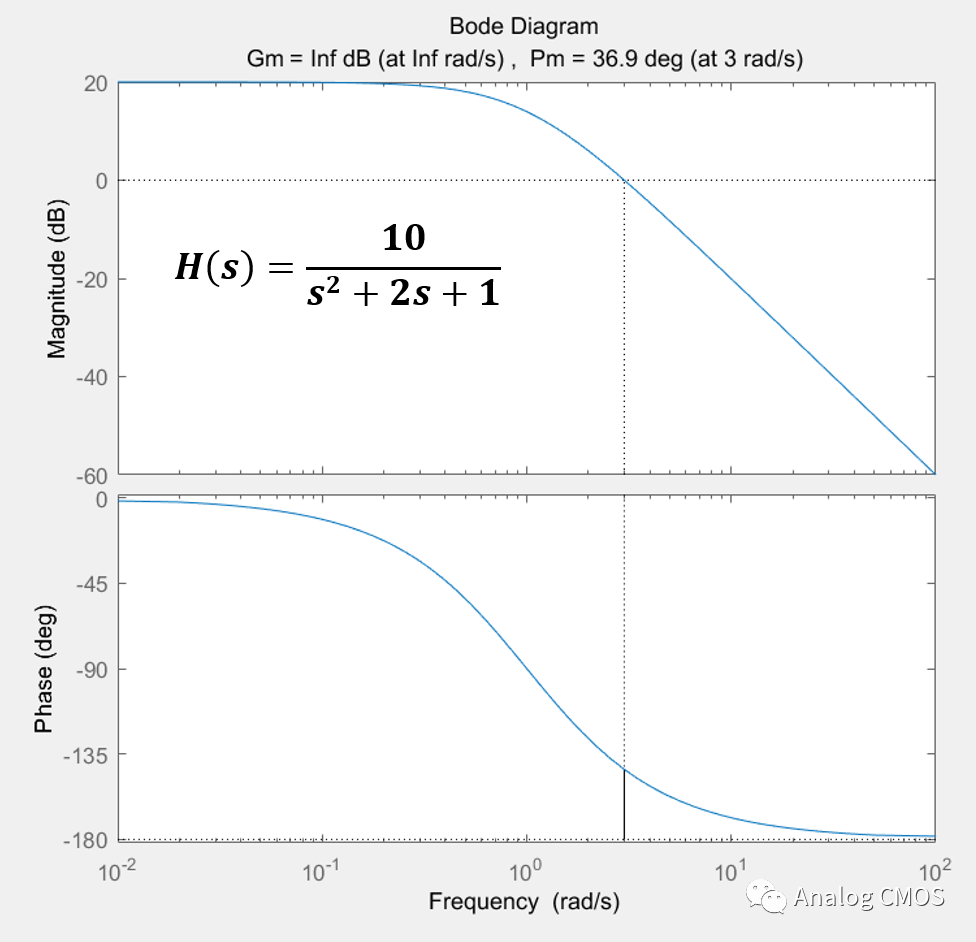
伯德图↓↓

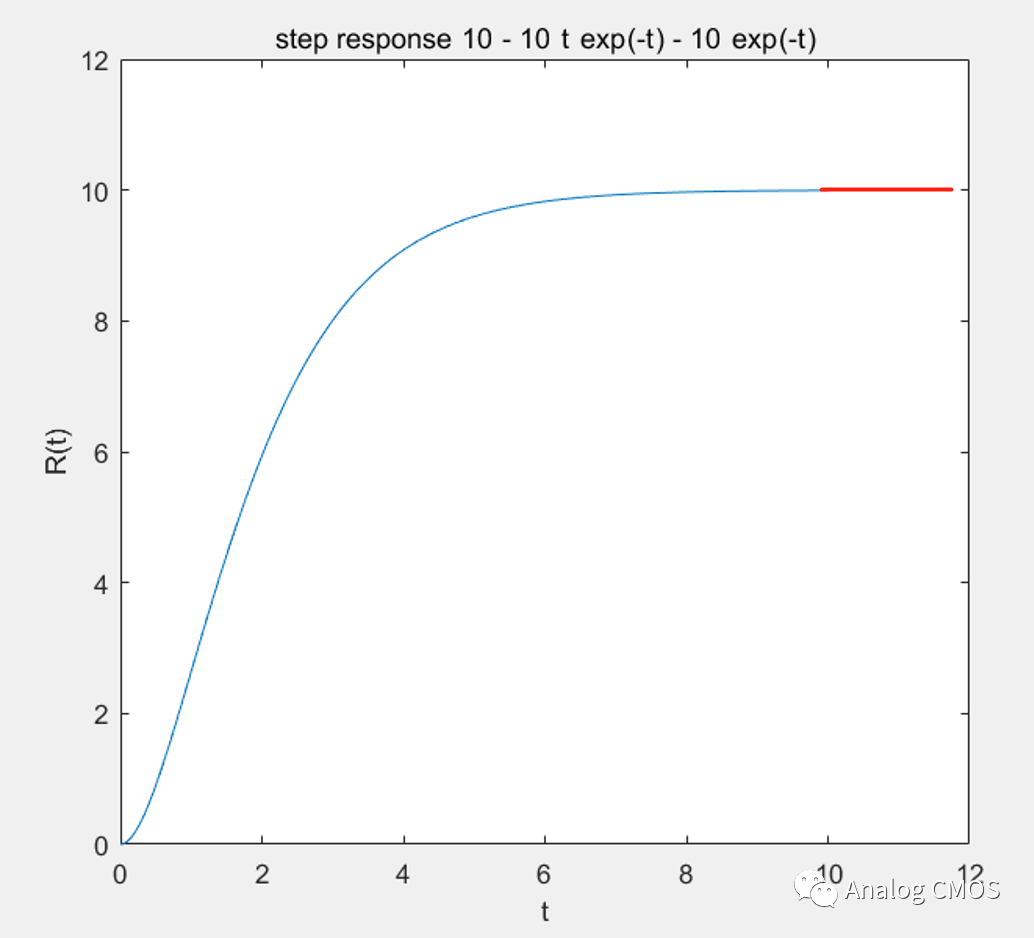
阶跃响应↓↓

阶跃响应的计算

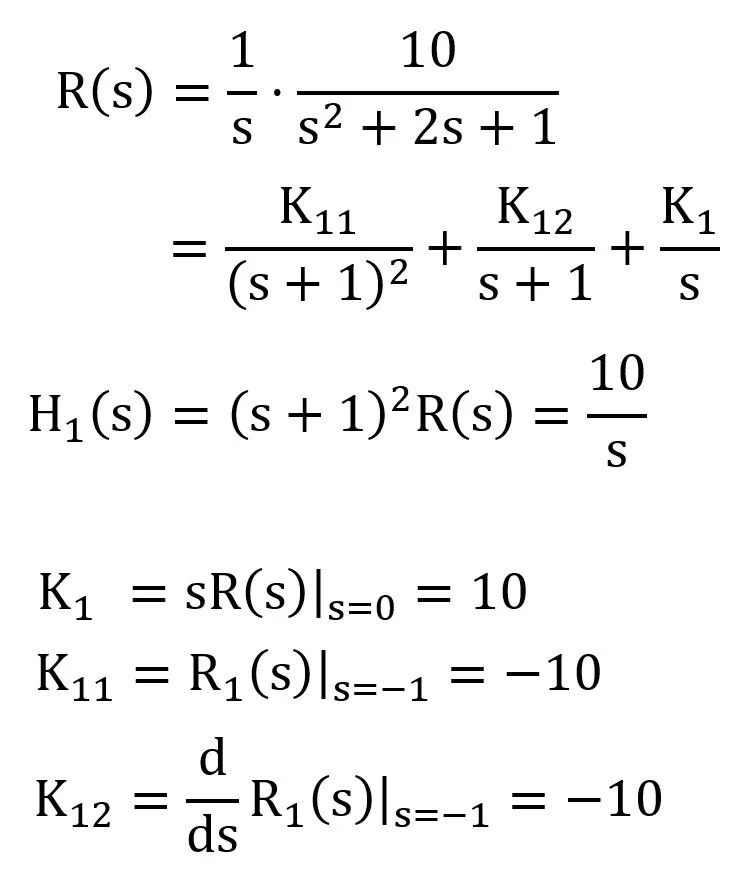
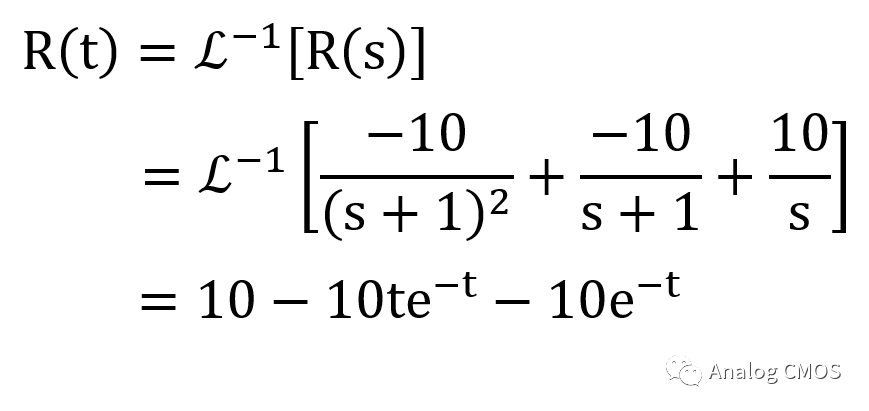
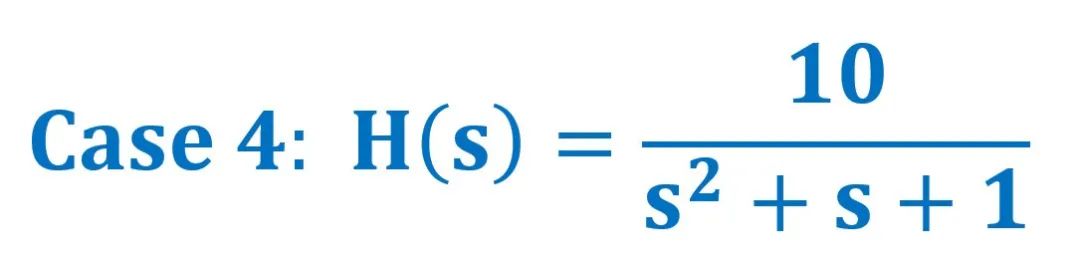
H(s)三维幅值坐标图↓↓

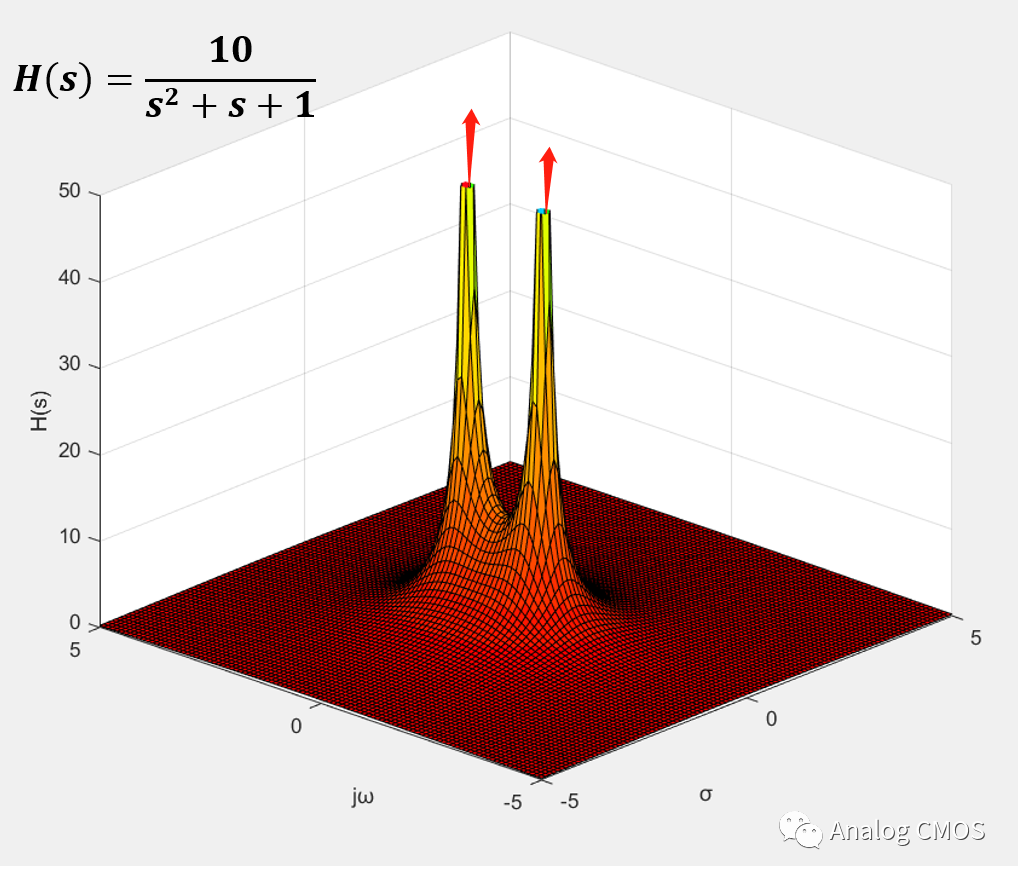
 s=jω时的剖面图↓↓

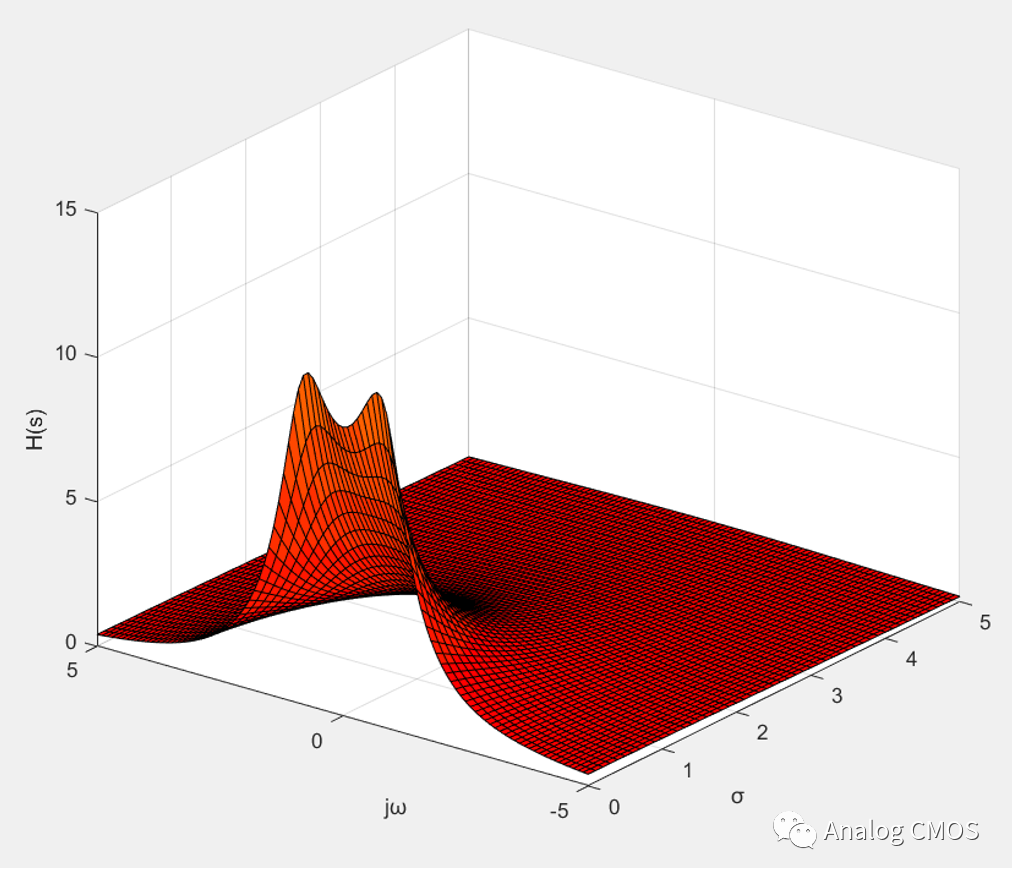
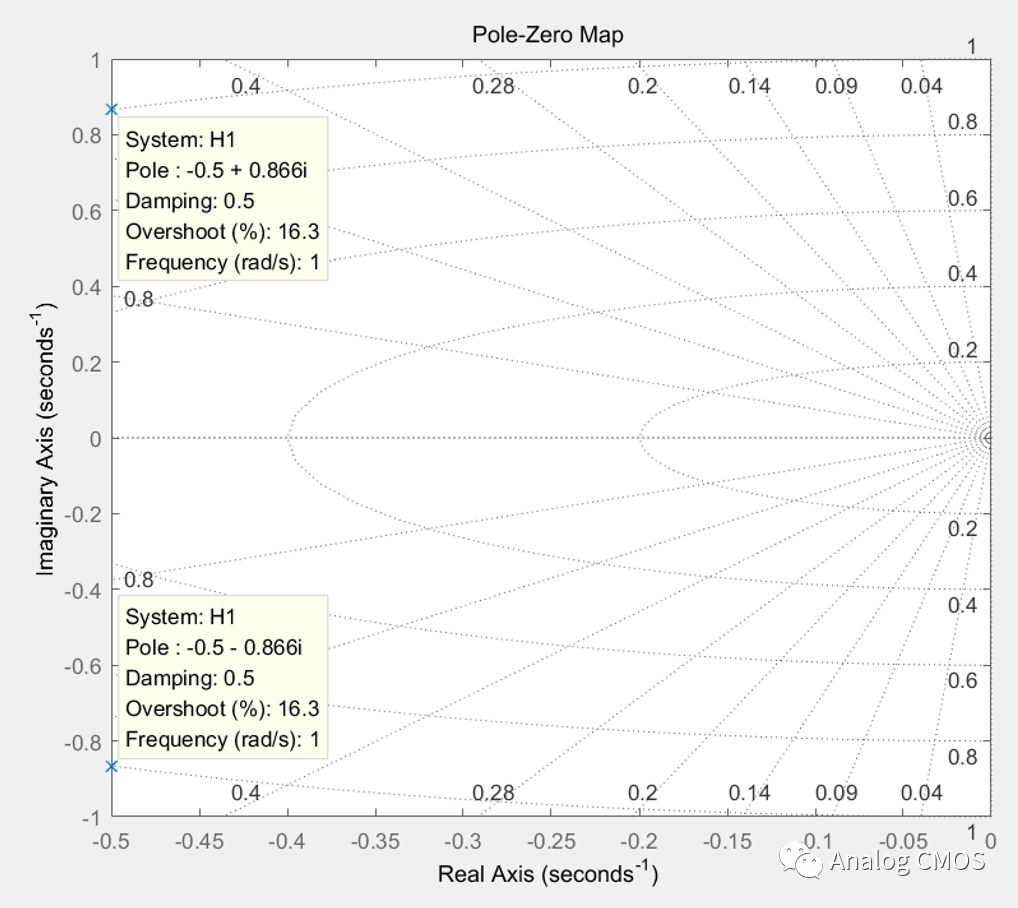
零极点图↓↓

伯德图↓↓

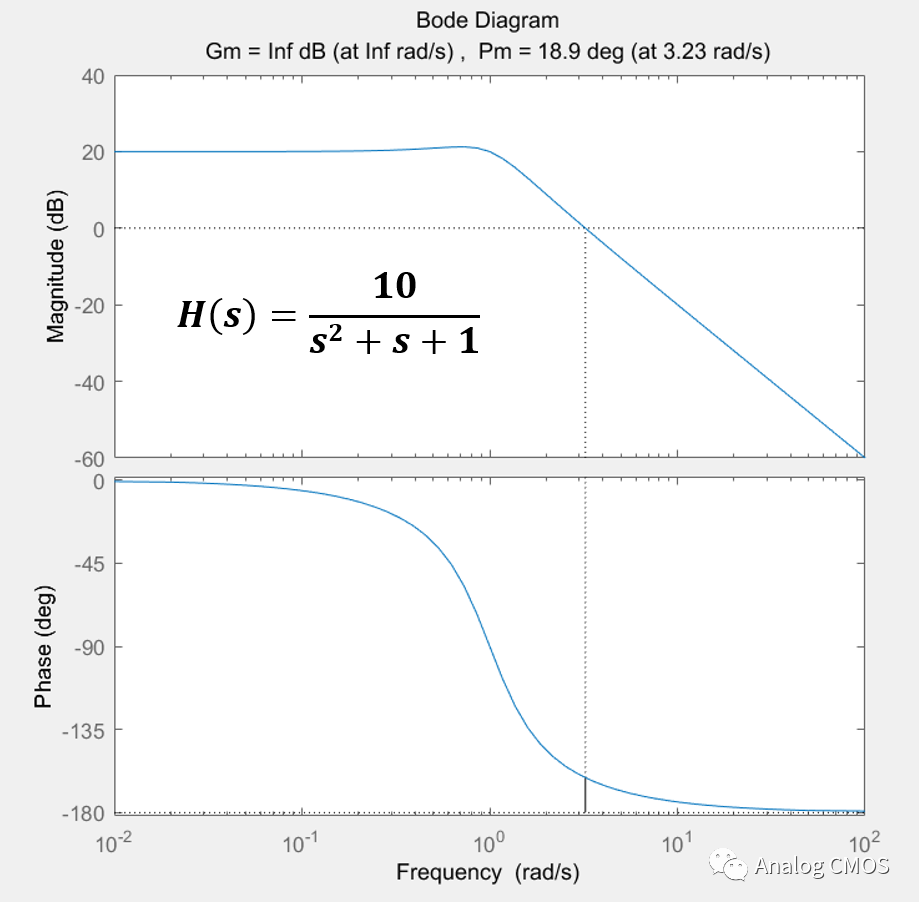
阶跃响应↓↓

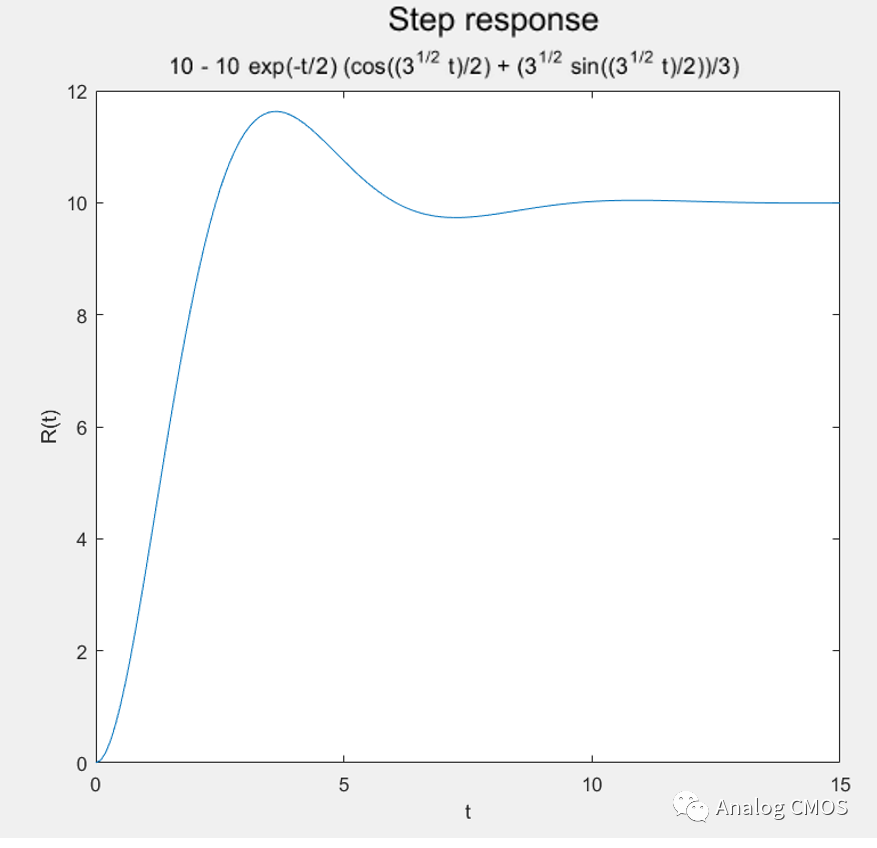
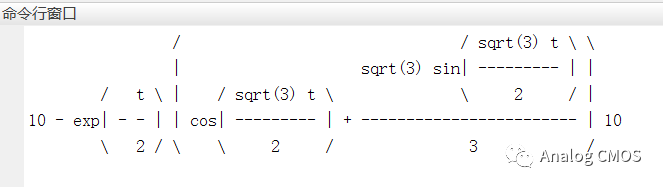
阶跃响应的计算: 结果见阶跃响应图标题

复杂的直接用matlab计算↓↓

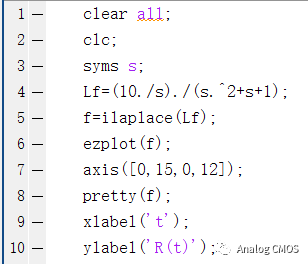
阶跃响应↓↓

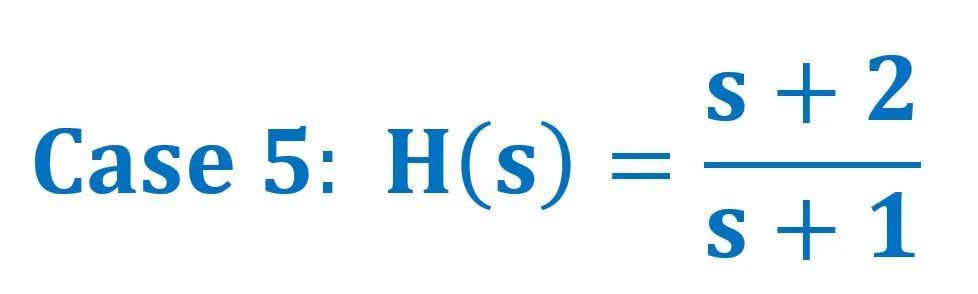
H(s)三维幅值坐标图 ↓↓

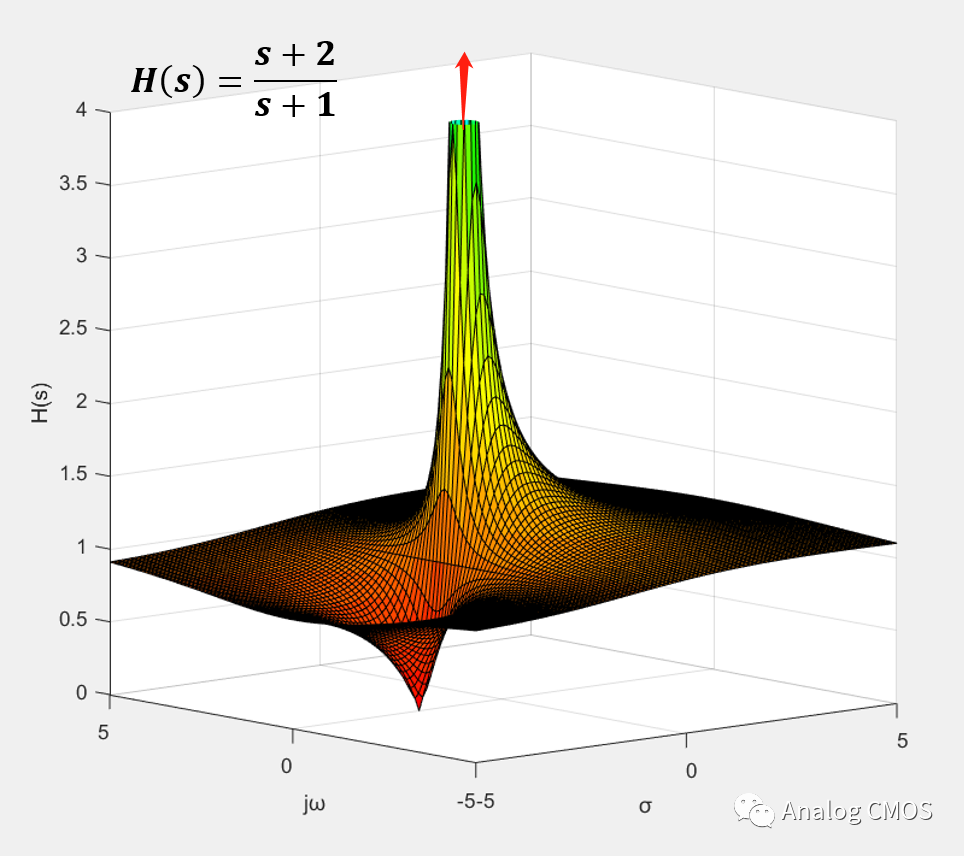
s=jω时的剖面图↓↓

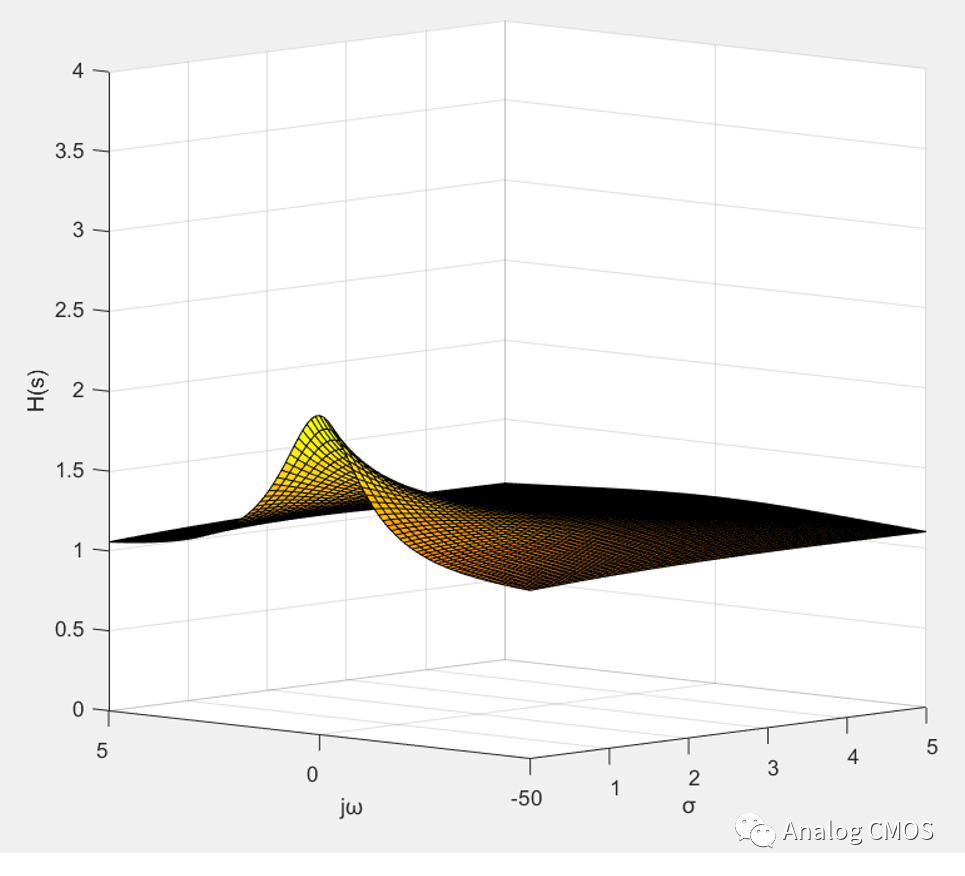
零极点图↓↓

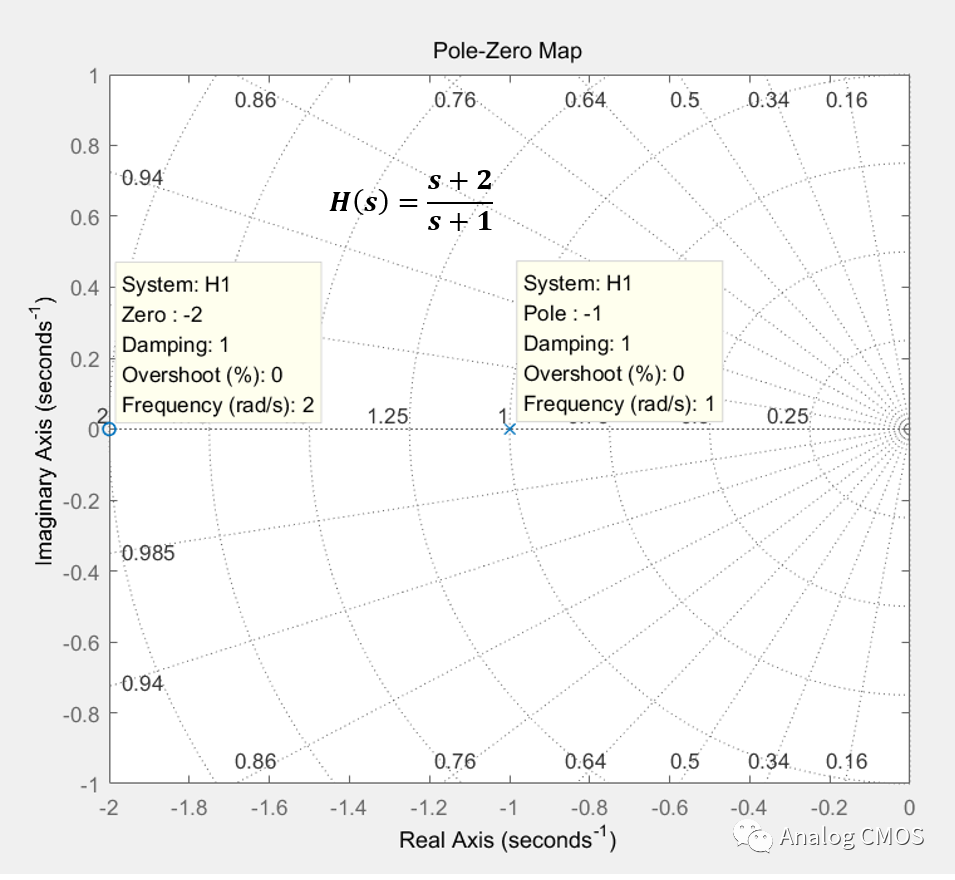
伯德图↓↓

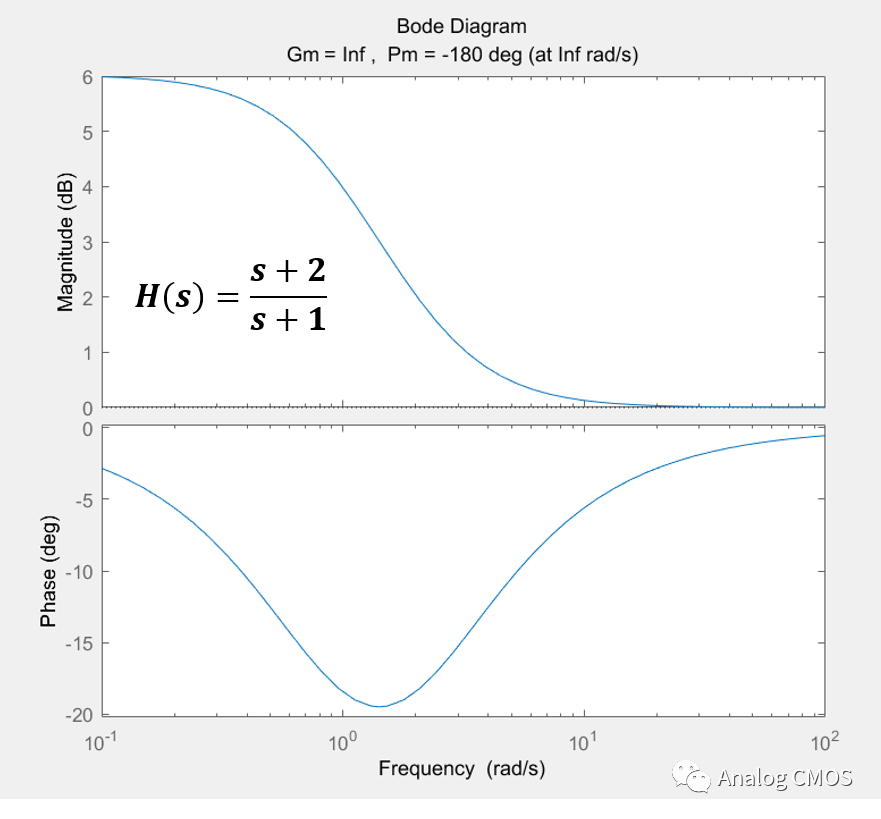
阶跃响应↓↓

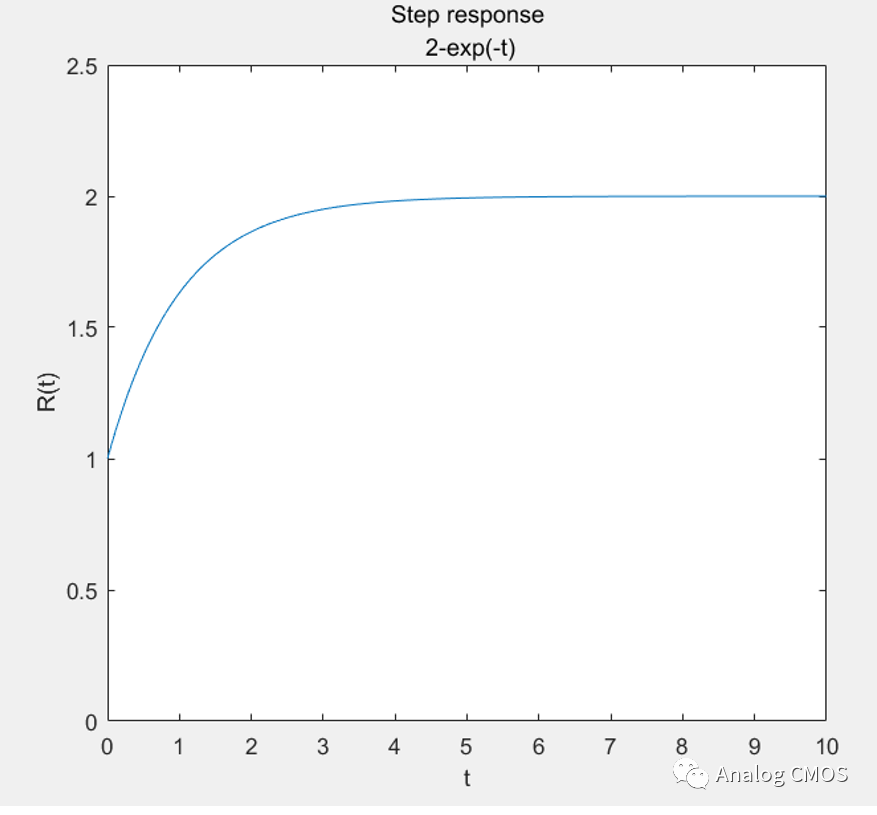
阶跃响应的计算：计算结果见阶跃响应坐标标题。

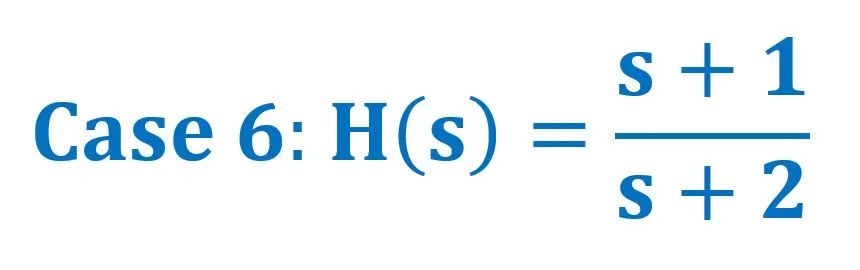
H(s)三维幅值坐标图 ↓↓

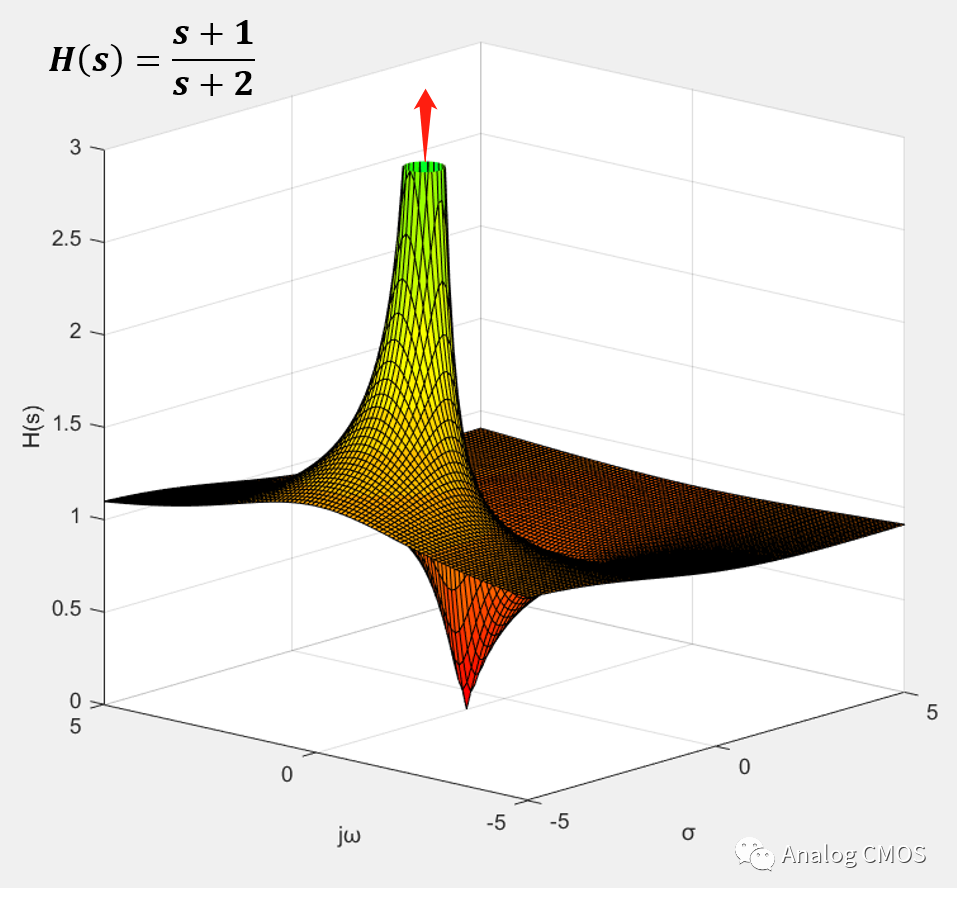
s=jω时的剖面图↓↓

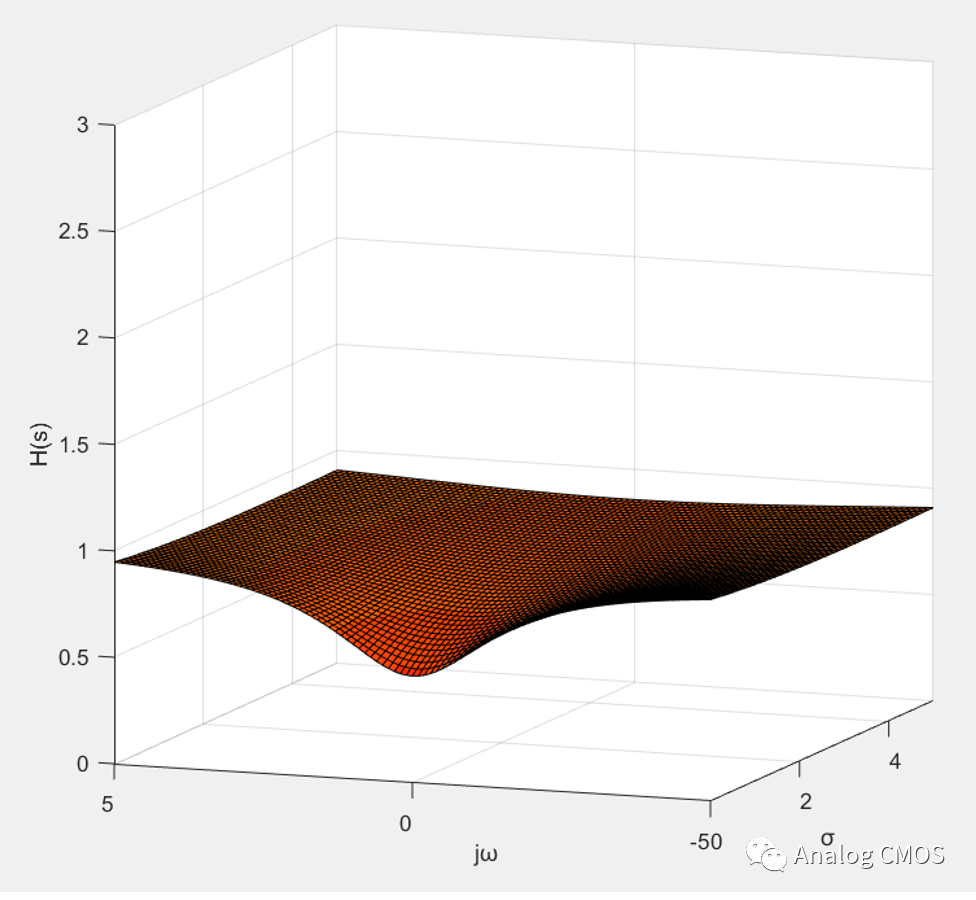
零极点图↓↓

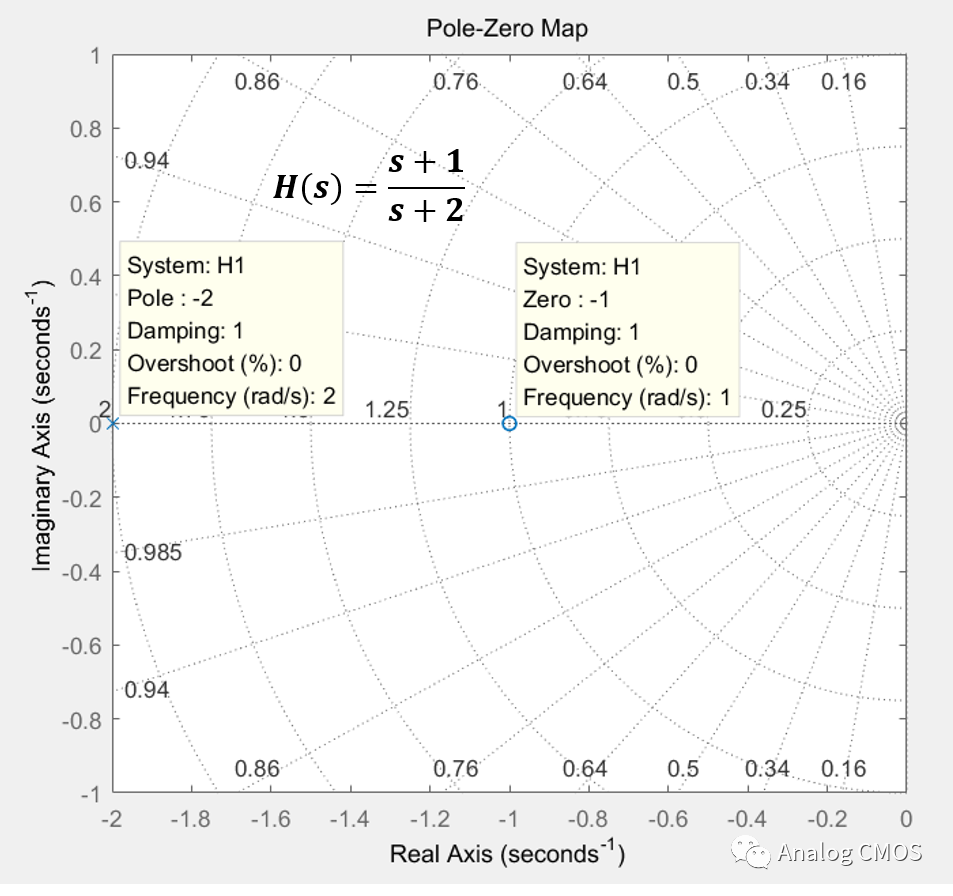
伯德图↓↓

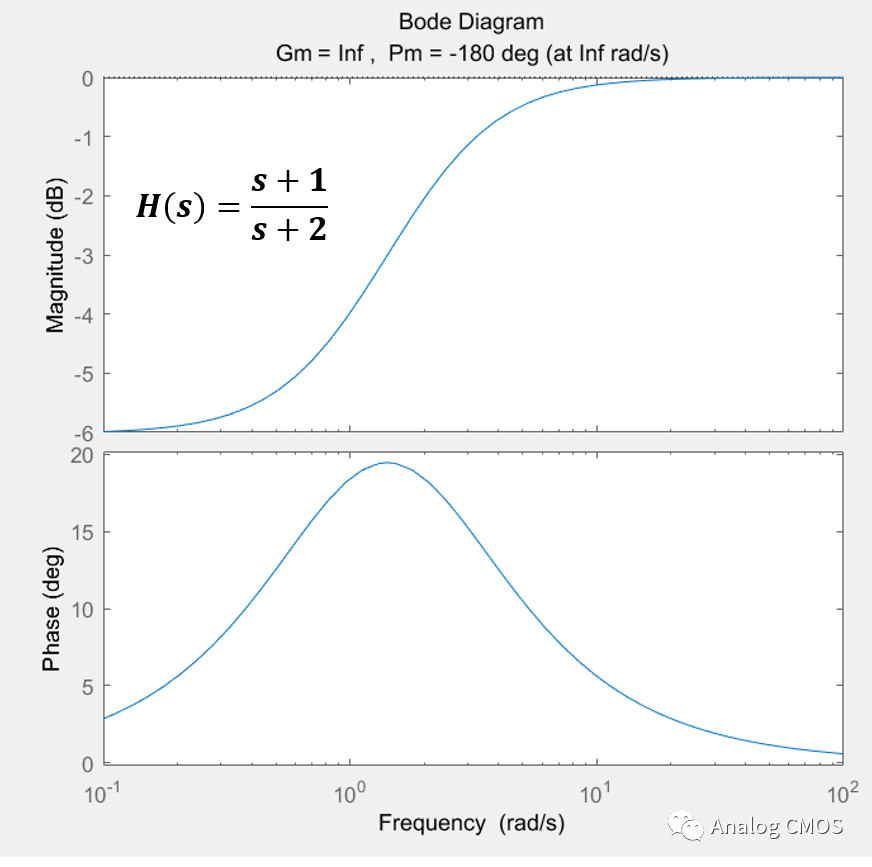
阶跃响应↓↓

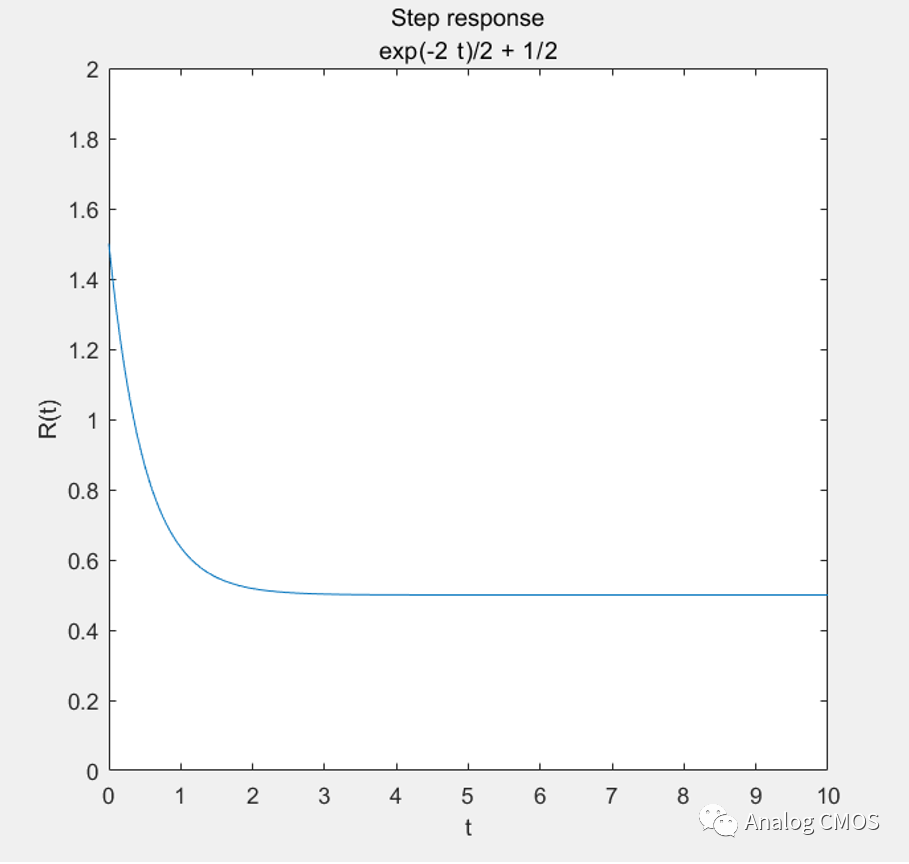
阶跃响应的计算：结果见阶跃响应坐标标题

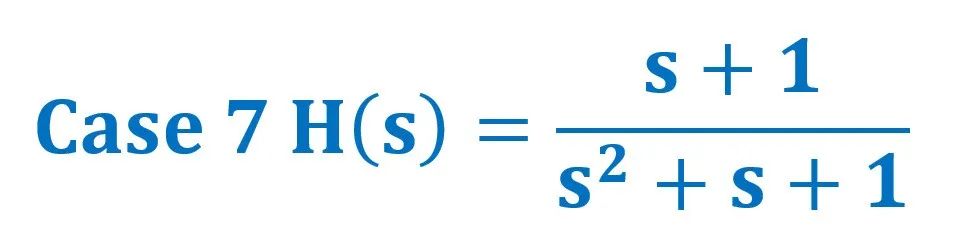
H(s)三维幅值坐标图 ↓↓

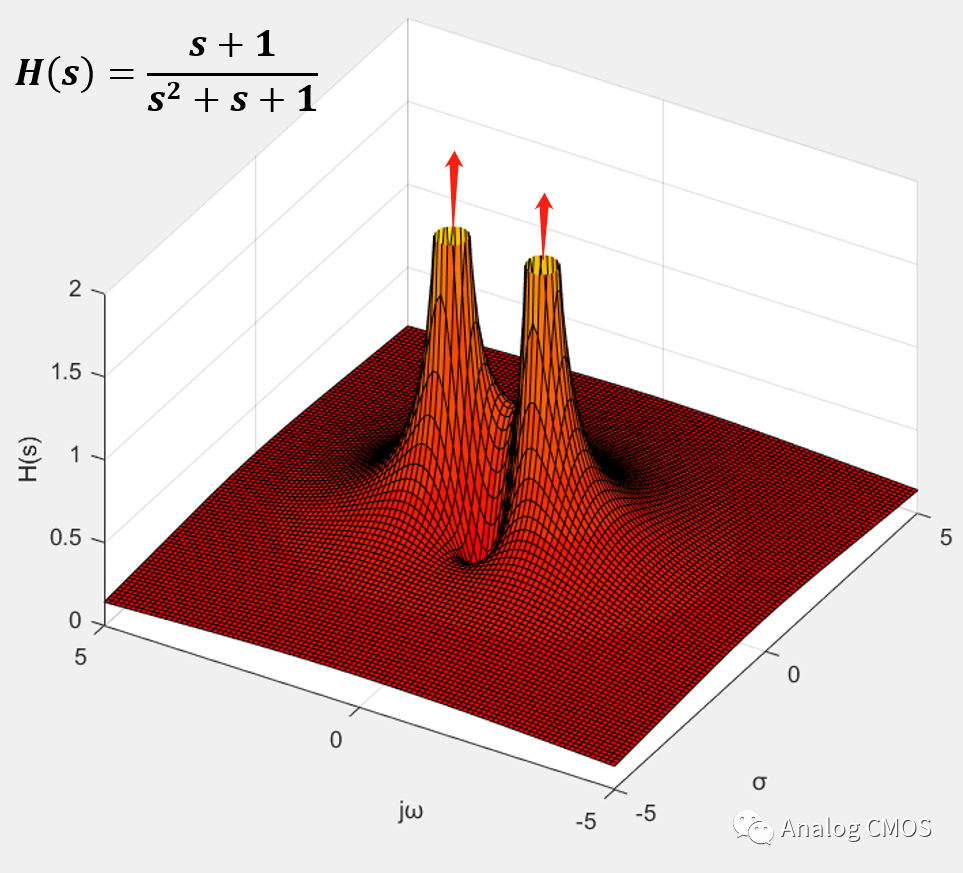
s=jω时的剖面图↓↓

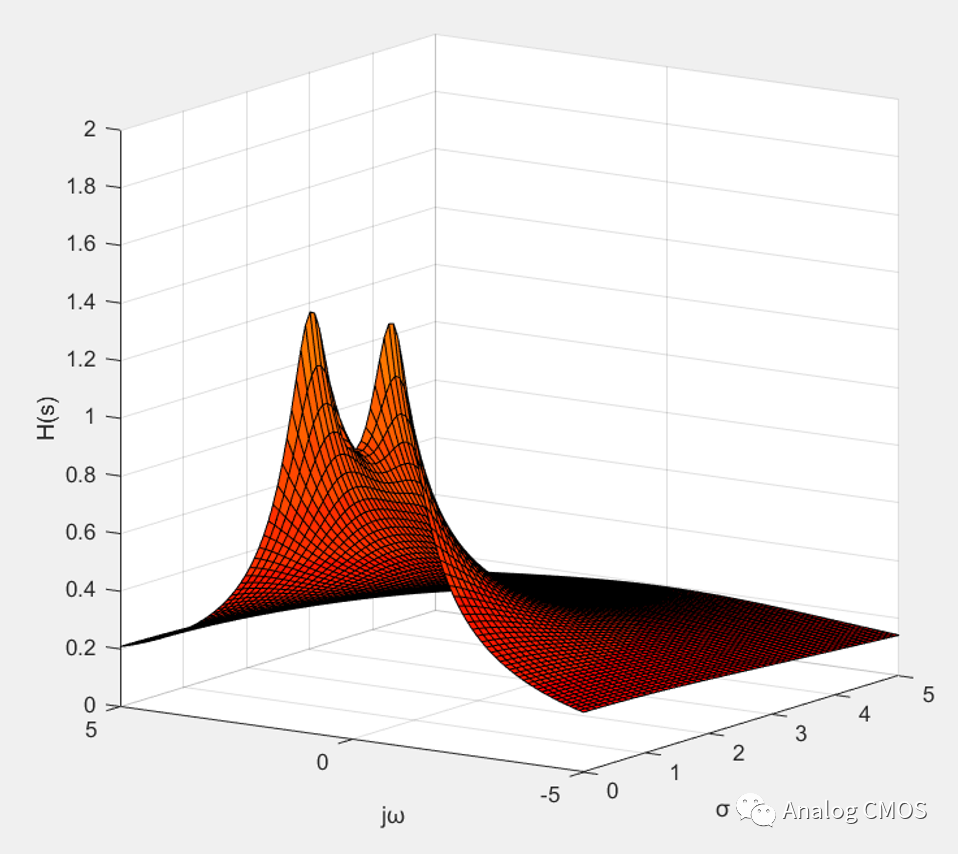
零极点图↓↓

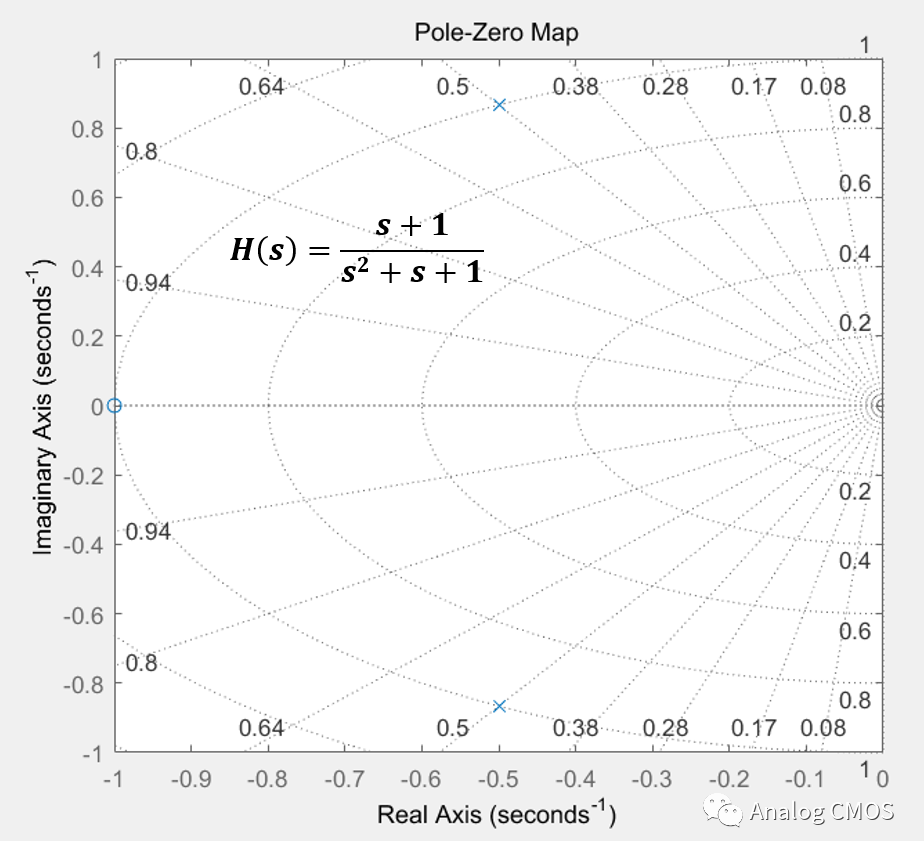
伯德图↓↓

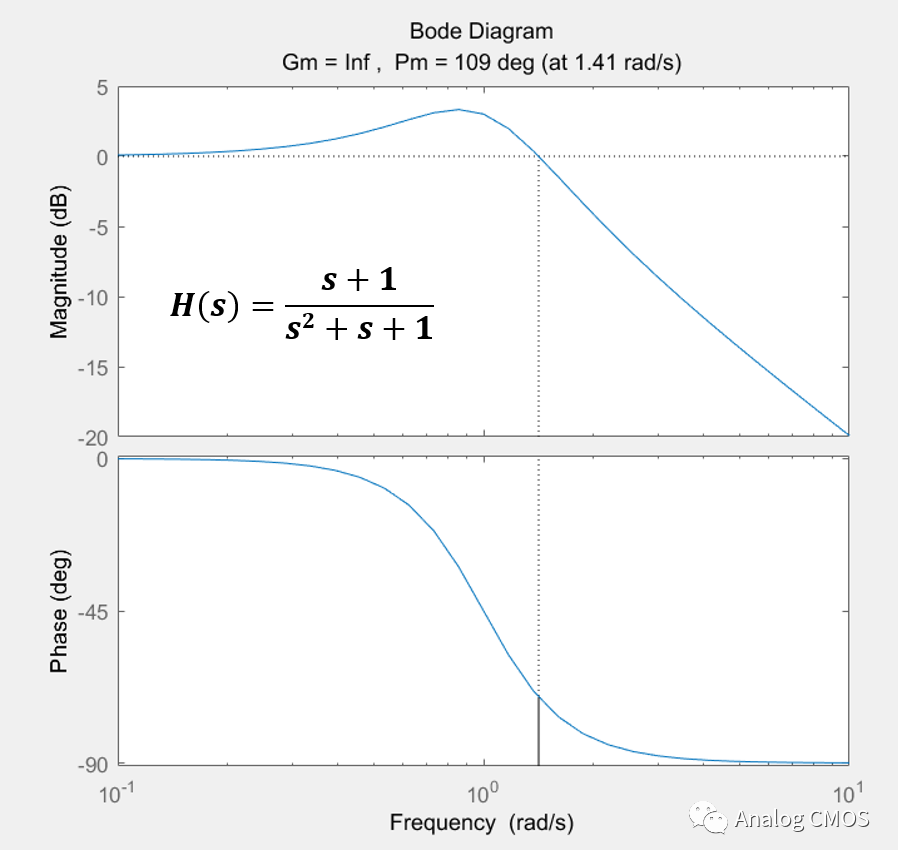
阶跃响应↓↓

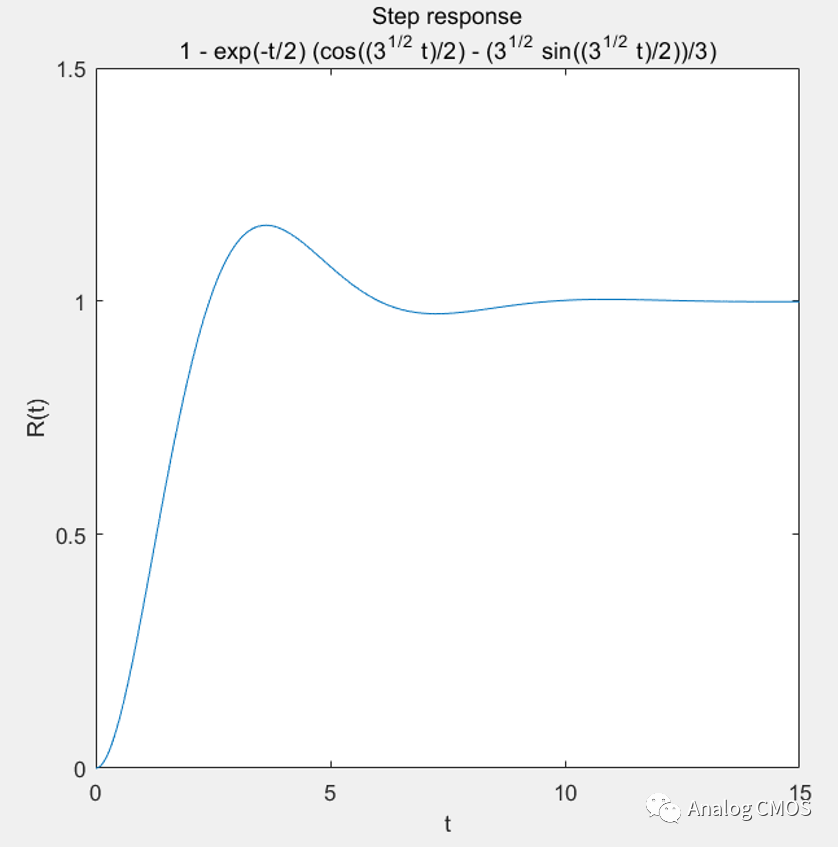
阶跃响应的计算：结果见阶跃响应坐标标题

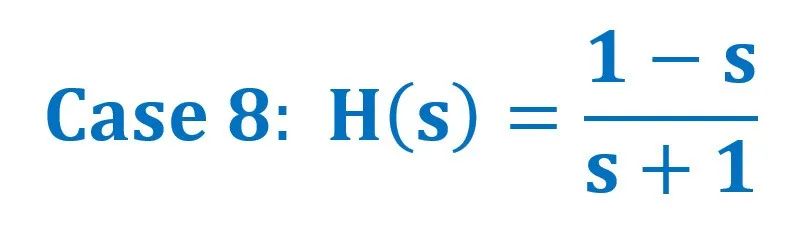
H(s)三维幅值坐标图 ↓↓

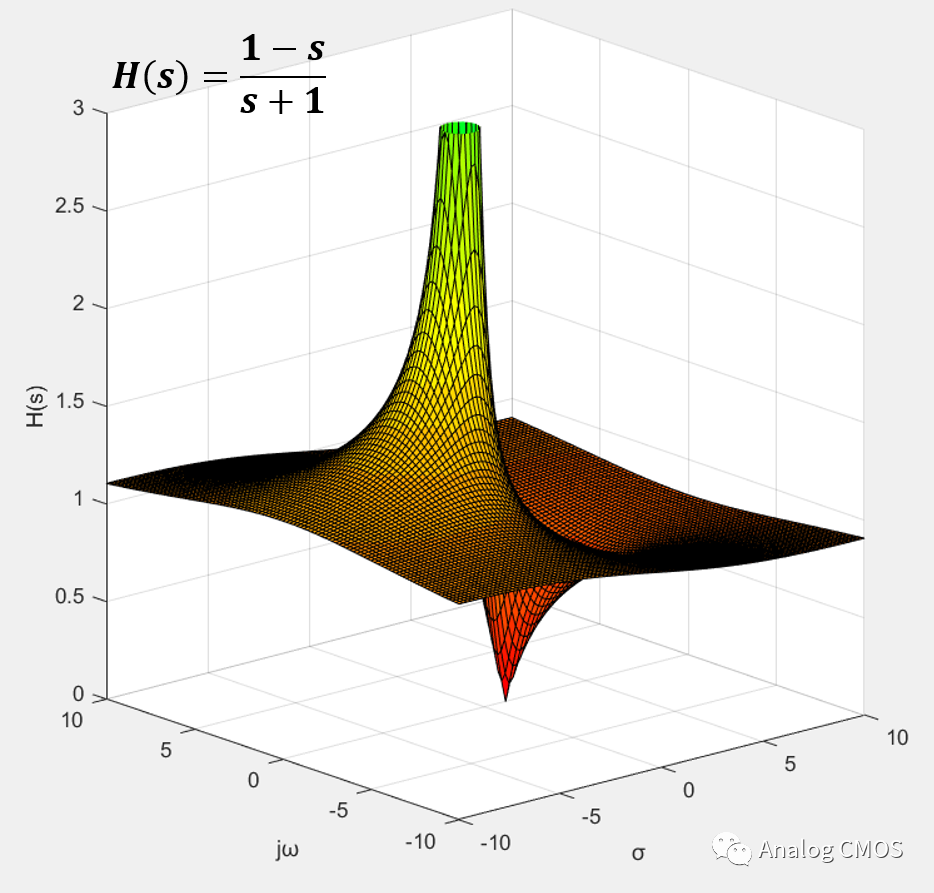
s=jω时的剖面图↓↓

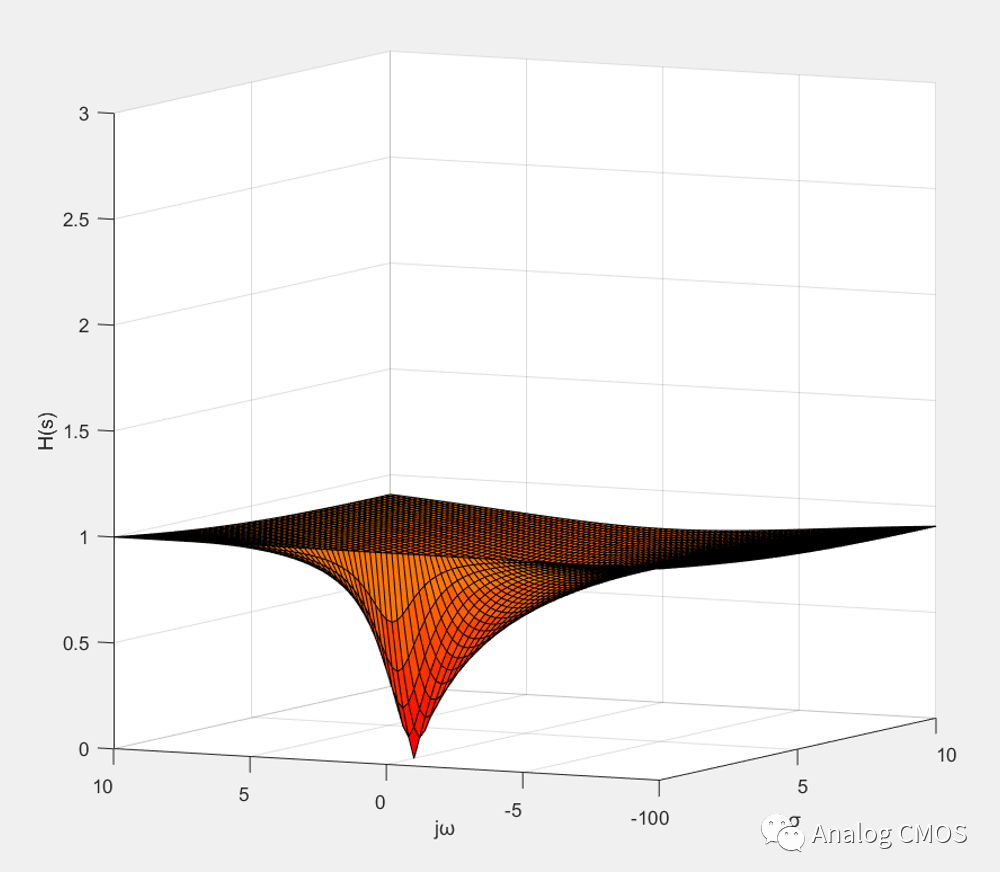
零极点图↓↓

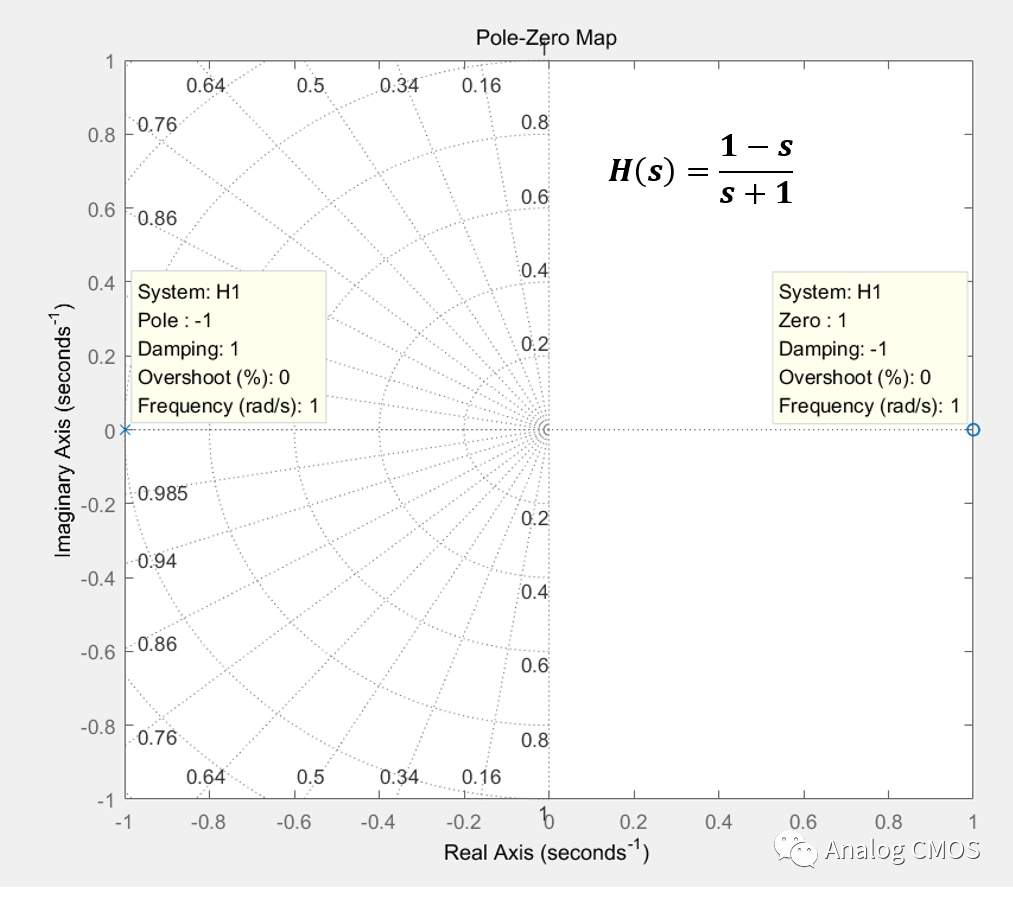
伯德图↓↓

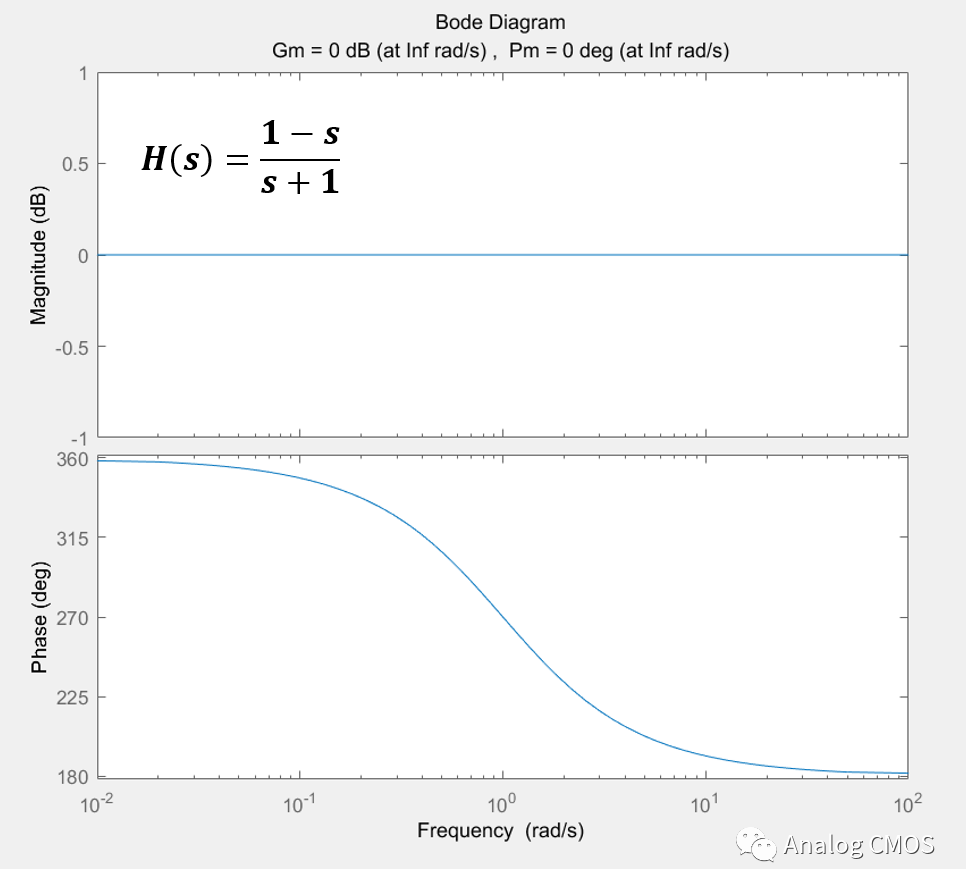
阶跃响应↓↓

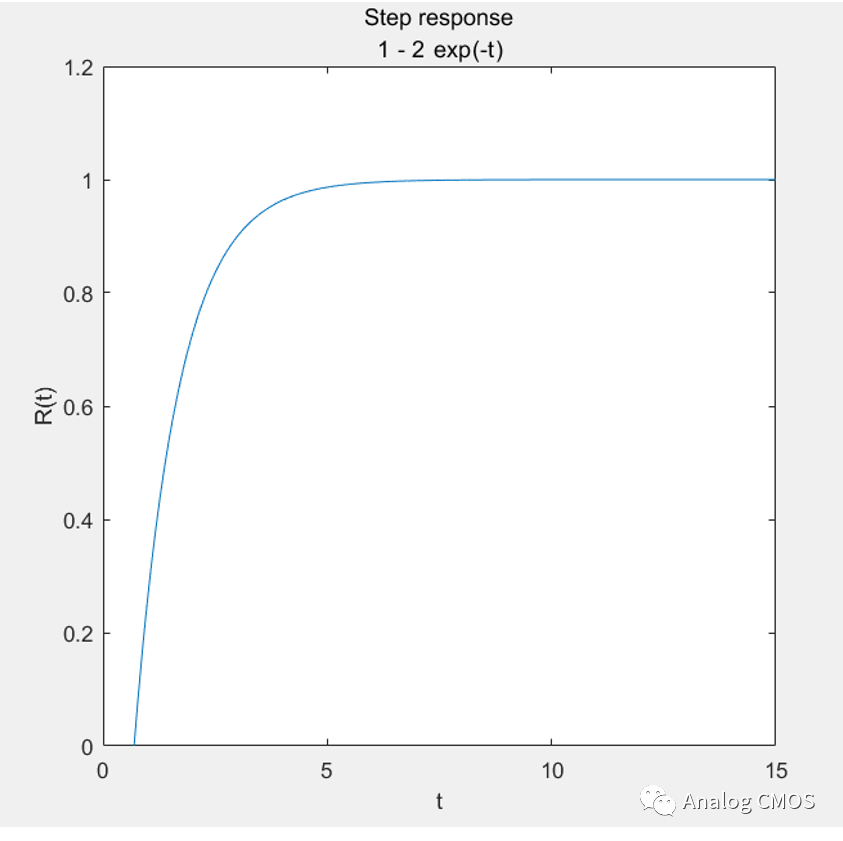
 如有不严谨 请见谅 

欢迎关注本公众号：Analog CMOS

右下角“在看”“点赞”