Simulink与控制系统仿真笔记05

5.时域分析法

5.1引言

以拉普拉斯变化为工具，从传递函数出发，直接在时间域上研究自动控制系统的性能的方法。常见的方法是根轨迹法和频率法

5.2时域响应分析

时域响应是指系统在外部输入作用下的输出过程

5.2.1典型输入

典型的输入信号有：

脉冲输入、阶跃输入、斜坡输入、加速度输入和正弦输入，利用这些典型的输入信号易于对系统进行试验和数学分析。

1.单位脉冲输入
KaTeX parse error: Undefined control sequence: matrix at position 30: … (t) = left{ ̲m̲a̲t̲r̲i̲x̲{ infty ,t =…
其中：
$$\underset{-\infty }{\overset{+\infty }{\int }}\delta (t)dt=1$$
其中拉氏变换是：
$$R(s)=L\left[\delta (t)\right]=1$$
实际中常用系统收到单位脉冲输入作用后的输出来衡量系统的暂态响应特性

单位脉冲响应的拉屎变化就是系统的传递函数。如果在系统的输入加一单位脉冲函数，由输出响应即可求出系统的传递函数。

2.单位阶跃输入
KaTeX parse error: Undefined control sequence: matrix at position 24: …1(t) = left{ ̲m̲a̲t̲r̲i̲x̲{ 1,t > 0 hf…
其拉斯变化：
$$R(s)=L\left[1(t)\right]=\frac{1}{s}$$
对于恒值系统相当于给定值突变，对于隧洞系统，相当于加一个突变的给定位置

3.单位斜坡输入
KaTeX parse error: Undefined control sequence: matrix at position 17: …r(t) = left{ ̲m̲a̲t̲r̲i̲x̲{ t,t > 0 hf…
其拉氏变换：
$$R(s)=L\left[r(t)\right]=\frac{1}{s^2}$$
对于随动系统，相当于加一个恒速变化的位置信号

4.单位加速速度输入
KaTeX parse error: Undefined control sequence: matrix at position 17: …r(t) = left{ ̲m̲a̲t̲r̲i̲x̲{ {1 over 2}…
其拉氏变换：
$$R(s)=L\left[r(t)\right]=\frac{2}{s^3}$$
对于随动系统，相当于加一个恒加速变化的位置信号

5.单位正弦输入
KaTeX parse error: Undefined control sequence: matrix at position 17: …r(t) = left{ ̲m̲a̲t̲r̲i̲x̲{ sin (t),t …
利用正弦信号可以求得系统对不同频率的稳态响应，由此间接判断系统性能。

• 对于恒值系统常使用阶跃输入
• 对于随动系统常用斜坡输入和加速度输入
• 对于扰动系统常用阶跃输入和脉冲输入

5.2.2线性系统响应一般求法

已知系统的传递函数：
$$G(s)=\frac{C(s)}{R(s)}=\frac{k_0(s+z_1)(s+z_2)...(s+z_m)}{(s+p_1)(s+p_2)...(s+p_m)}$$
且输入为：
$$R(s)=\frac{k_r(s+z_{r1})(s+z_{r2})...(s+z_{rm})}{(s+p_{r1})(s+p_{r2})...(s+p_{rm})}$$
其中：$$-z_{r1}$$,$$-z_{r2}$$…$$-z_{rm}$$是输入零点，$$-p_{r1}$$,$$-p_{p2}$$…$$-p_{rm}$$

是输入极点。

那么相应的传递函数为，
$$C(s)=R(s)\cdot G(s)=\frac{k_0{k}_r(s+z_1)(s+z_2)...(s+z_m)(s+z_{r1})(s+z_{r2})...(s+z_{rm})}{(s+p_1)(s+p_2)...(s+p_m)(s+p_{r1})(s+p_{r2})...(s+p_{rm})}$$

5.2.2.1G(s)无重极点的情况

5.2.2.2G(s)有重极点的情况

5.2.3时域响应的性能指标

5.2.3.1阶跃响应的性能指标

当已知时域系统的响应信号的$$c(t)$$，按照$$c(t)$$的形状基本就可以判断出其动力学的优劣，一般来说对于时域响应的要求有两个基本要求和三个衡量的标准来概括：

两个基本要求：对设定值输入的跟随，对扰动输入的抑制

三个平衡量标准：跟随和抑制过程的稳定性和准确性。

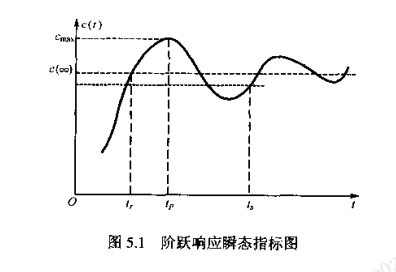
5.2.3.2误差积分指标

5.2.4MATLAB/Simulink在时域分析中的应用

时域分析，尤其是在高阶系统的分析，其困难点主要是在系统的极点，留数的获取上，以及在已知响应表达式的基础上，如何绘制响应的波形和求取性能指标等一系列问题。

5.2.4.1时域分析中的MATLAB函数的应用

1.step()函数的用法

y=step(num,den,t)

step(num,den)

step(num,den,t)

step(A,B,C,D,iu,t)

2.impluse()函数的用法

3.常用的时域分析函数

covar：连续系统对白噪声的方差响应

initial：连续系统的零输入响应

1sim：连续系统对任意输入的响应

对于离散系统在 前面加“d”

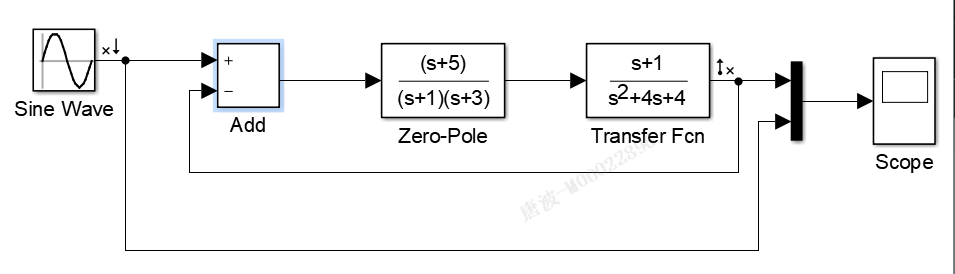
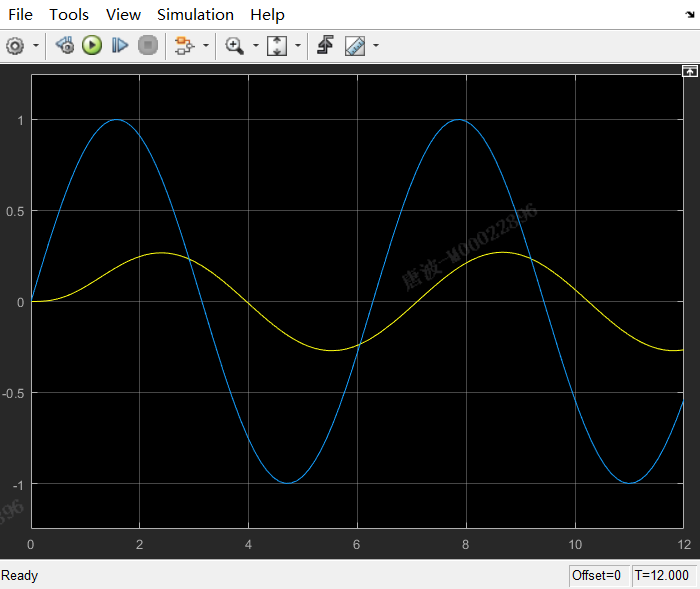
5.2.4.2MATLAB在时域分析中的应用举例

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kOiitXeD-1658734634910)(https://raw.githubusercontent.com/yumo2021/PicGo1/main/20220530150721.png)]

>> clear
>> num=[1];
>> den=[1,0.4,1];>> t=[0:0.1:10];
>> [y,x,t]=step(num,den,t);
>> plot(t,y)
>> hold on 
>> grid
>> xlabel('Time[sec] t')
>> ylabel('y')

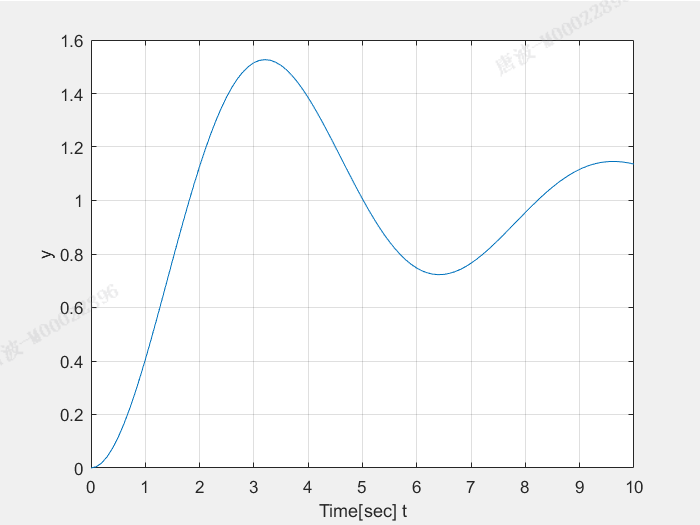
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-f9E34C43-1658734634912)(https://raw.githubusercontent.com/yumo2021/PicGo1/main/20220530150739.png)]

>> num=[1];
>> den=[1 0.3 1];
>> t=[0:0.1:10];
>> u=t;
>> [y,x]=lsim(num,den,u,t);
>> plot(t,y,'b');
>> grid
>> xlabel('Time');
>> ylabel('Y');

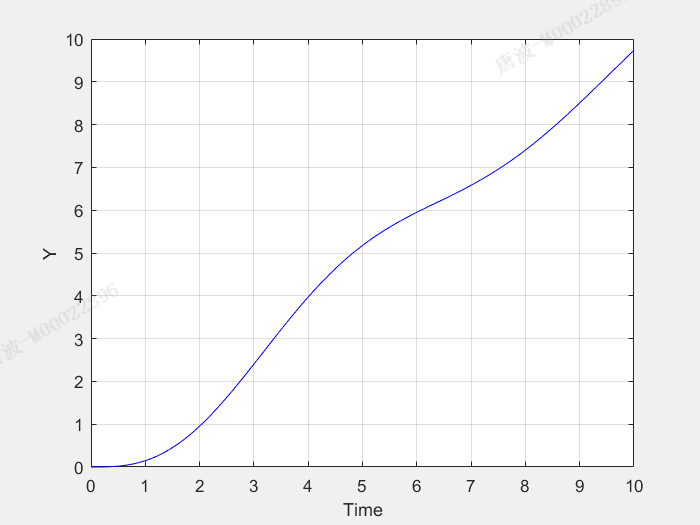
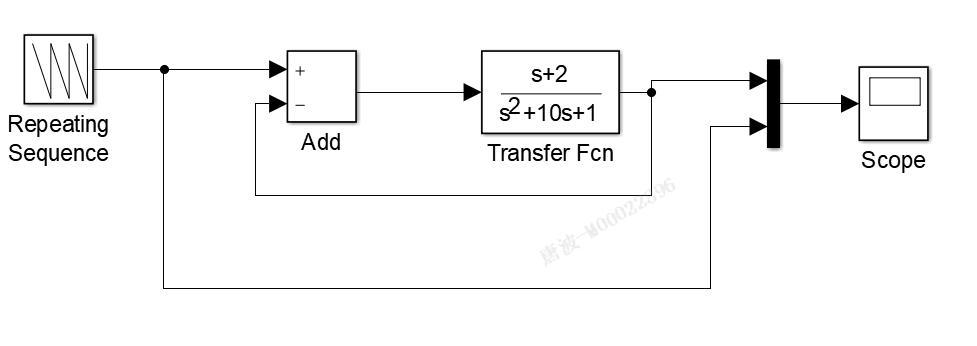
>> numg=[1,2];
>> deng=[1,10,1];
>> [num,den]=cloop(numg,deng,-1);
>> v1=[0:0.1:1];		%分三段绘制三角波
>> v2=[0.9:-0.1:-1];
>> v3=[-0.9:0.1:0];
>> u=[v1,v2,v3];
>> t=[0:0.1:4];
>> [y,x]=lsim(num,den,u,t);
>> plot(t,y,t,u);
>> xlabel('Time');
>> ylabel('Y');

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qGrpWi9V-1658734634915)(https://raw.githubusercontent.com/yumo2021/PicGo1/main/20220530154520.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AtthAfAQ-1658734634915)(https://raw.githubusercontent.com/yumo2021/PicGo1/main/20220530160049.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fcrLS5Mr-1658734634916)(https://raw.githubusercontent.com/yumo2021/PicGo1/main/20220530160944.png)]

5.2.5一阶和二阶系统的时域响应分析

5.2.5.1一阶系统分析

一阶微分方程称为一阶系统，其传递函数为：
$$G_{(s)}=\frac{K}{Ts+1}$$
其中，$$T$$成为一阶系统的时间常数，$$G(s)$$可写成：
$$G_{(s)}=\frac{C_{(s)}}{R_{(s)}}$$
当$$r(t)=1$$时，一阶系统的输出从$$C(t)$$称为单位阶跃响应

此时，
$$R_{(s)}=\frac{1}{s}$$

$$C_{(s)}=G_{(s)}{R}_{(s)}=\frac{K}{s(Ts+1)}=K(\frac{1}{s}-\frac{1}{s+\frac{1}{T}})$$

反拉斯变换得：
$$C_{(t)}=K(1-e^{-\frac{1}{T}})$$
一阶系统的闭环极点$$\frac{-1}{T}$$，位于负实轴上：

• 阶跃响应是单调的
• 闭环极点离虚轴越远，响应越快

5.2.5.2二级系统的分析

典型二阶系统的结构如图所示，

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ezbkVT2X-1658734634917)(https://raw.githubusercontent.com/yumo2021/PicGo1/main/20220531215958.png)]

其闭环传递函数$$G(s)$$为：
$$G_{(s)}=\frac{{{\omega }_n}^2}{s^2+2\xi {\omega }_n+{{\omega }_n}^2}$$

$$G_{(s)}=\frac{1}{T^2{s}^2+2\xi T+1},T=\frac{1}{{\omega }_n}$$

$${\omega }_n$$为自然角频率，或者固有频率，$$\xi$$为阻尼系数，$$T=\frac{1}{{\omega }_n}$$为 振荡周期

系统特征方程（分母为零）：$$s^2+2\xi {\omega }_n+{{\omega }_n}^2$$

特征根：$$s_{1,2}=-\xi {\omega }_n\pm {\omega }_n\sqrt{{\xi }^2-1}$$

因此系统的两个极点：$$p_{1,2}=-\xi {\omega }_n\pm {\omega }_n\sqrt{{\xi }^2-1}$$

5.2.5.3二级系统参数对时域响应性能的影响

1.闭环参数$${\omega }_n$$和$$\xi$$的影响

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wfwbCN0n-1658734634917)(https://raw.githubusercontent.com/yumo2021/PicGo1/main/20220531221555.png)]

>> wn=1;
>> sigma=[0,0.2,0.4,0.6,0.9,1.2,1.5];
>> num=wn*wn;
>> t=linspace(0,20,200)
for j=1:7
den=conv([1,0],[1,2*wn*sigma(j)])
s1=tf(num,den)
sys=feedback(s1,1);
y(:,j)=step(sys,t)
end
>> plot(t,y(:,1:7))
>> plot(t,y(:,1:7))
>> grid
>> gtext('sigma=0')
>> gtext('sigma=0.2')
>> gtext('sigma=0.4')
>> gtext('sigma=0.6')
>> gtext('sigma=0.9')
>> gtext('sigma=1.2')
>> gtext('sigma=1.5')

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DVTdUkem-1658734634917)(https://raw.githubusercontent.com/yumo2021/PicGo1/main/20220531222402.png)]

从图中可以明显看出，在$$\xi$$为0.4~0.9的范围内，系统上升较快，而超调又不大，股灾 一般的工程系统中，$$\xi$$就选在这个范围内。其中尤其$$\xi =\frac{\sqrt{2}}{2}$$时响应较快。

2.开环参数$$K$$和$$T$$的影响

对于一般的二阶系统而言，通过适当的变换，其闭环传递函数表示为：
$$G(s)=\frac{C(s)}{R(s)}=\frac{\frac{K}{T}}{s^2+\frac{1}{T}s+\frac{K}{T}}=\frac{K}{T{s}^2+s+K}=\frac{\frac{K}{s(Ts+1)}}{1+\frac{K}{s(Ts+1)}}$$
对比于二阶系统的典型传递函数，可设$$\frac{K}{T}={{\omega }_n}^2$$，$$\frac{1}{T}=2\xi {\omega }_n$$，即$${\omega }_n=\sqrt{\frac{K}{T}}$$

一般结论：$$T$$越小，则$${\omega }_n$$越大，$$\xi$$越大，系统的快速性和稳定性同时转好，但是在实际系统中用$$T$$来改善系统性能的作用是有限的。

另一方面，$$K$$越大，则$${\omega }_n$$越大，而$$\xi$$越小，表明$$K$$对快速性和相对稳定性的影响是矛盾的，实际只能折中处理。

对一个二阶系统而言，应有$$K=\frac{1}{2T}=\frac{{\omega }_n}{2}$$，称之为二阶最佳参数关系。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9o1nhCXw-1658734634918)(https://raw.githubusercontent.com/yumo2021/PicGo1/main/20220602095719.png)]

T=1
k=[0.1,0.2,0.5,0.8,1.0,2.4]
t=linspace(0,20,200)
num=[1]
den=conv([1,0],[T,1])
for j=1:6
s1=tf(num*k(j),den)	%负反馈
sys=feedback(s1,1)
y(:,j)=step(sys,t)
end
plot(t,y(:,1:6))
grid
gtext('k=0.1')
gtext('k=0.2')
gtext('k=0.5')
gtext('k=0.8')
gtext('k=1.0')
gtext('k=2.4')

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-G3gkZuSx-1658734634918)(https://raw.githubusercontent.com/yumo2021/PicGo1/main/20220602101720.png)]

5.2.5.4闭环极点分布对时域响应的影响

如果闭环极点落在虚轴上，则系统处于临界稳定状态

如果闭环极点是负实数极点，则系统阶跃响应是单调的，超调量$$\sigma =0$$。

如果闭环极点是负实部的共轭复数极点，则系统阶跃响应是衰减振荡的，其超调量与初始相位角$$\theta$$有关，$$\theta$$越大，超调量越大。

系统的时域响应的快速性与闭环极点距离虚轴的距离有关系，距离越大，则超调时间越小。

系统有多个闭环极点，则距离轴越近的闭环极点所起的作用越大，如果一个闭环极点距离虚轴的距离较另一个闭环极点距离大五倍以上，则距离远的闭环极点的影响可以忽略。

5.2.5.5改善系统时域响应性能的一些措施

如前文所述，单纯通过改变回路增益K来达到系统时域响应又快又稳是不可能的，只能做一个合理的折中。下面给出两种可以提高系统性能的方法。

1.输出微分反馈

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kzcSl9ws-1658734634918)(https://raw.githubusercontent.com/yumo2021/PicGo1/main/20220608195128.png)]

2.比例微分控制

5.2.6高阶系统的时域响应

5.2.6.1高阶系统时域响应的一般形式

设系统的闭环传递函数：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Eki4pt67-1658734634919)(https://raw.githubusercontent.com/yumo2021/PicGo1/main/20220608174824.png)]

5.2.6.2高阶系统的主导极点

结论：

1. 主导极点：在整个响应过程中，起决定性作用的是闭环极点，称之为主导极点，它是距虚轴最近而附近又没有闭环零点的闭环极点。工程上往往只是用主导极点来估算系统的动态特性，即将系统近似的看成一阶或者二阶系统。
2. 距离虚轴的距离较主导极点远5倍或者5倍以上的闭环零点、极点，其影响可以忽略不计。
3. 偶极子。一对靠得很近的闭环零点、极点称为偶极子。工程上，当某极点与某零点之间的距离比它们模值小一个数量级时，可认为这对零点、极点称为偶极子。偶极子对时域的影响可以忽略不记，在闭环传递函数中，如果零点和极点数值上相近则可以将该零点和极点一起消掉，称为偶极子相消。
4. 除了主导极点外，闭环零点的作用是使响应加快而超调增加，闭环极点的作用正好相反。

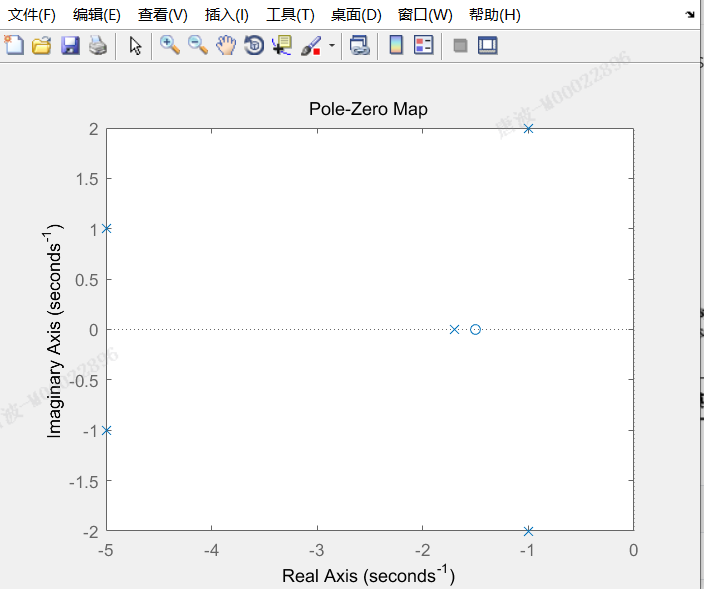
eg：

$$G_{(s)}=\frac{147.3(s+1.5)}{(s^2+2s+5)(s^2+10s+26)(s+1.7)}$$

k=147.3;
t=0:0.1:6;
num0=k*[1,1.5];
den00=[1,2,5];
den01=[1,10,26];
den02=[1,1.7];
sys0=tf(num0,conv(den00,conv(den01,den02)));
pzmap(sys0);%绘制零极点
y0=step(sys0,t);
num1=5;%这里是为了保证静态增益与原来函数一致
sys1=tf(num1,den00);
y1=step(sys1,t);%主导极点函数
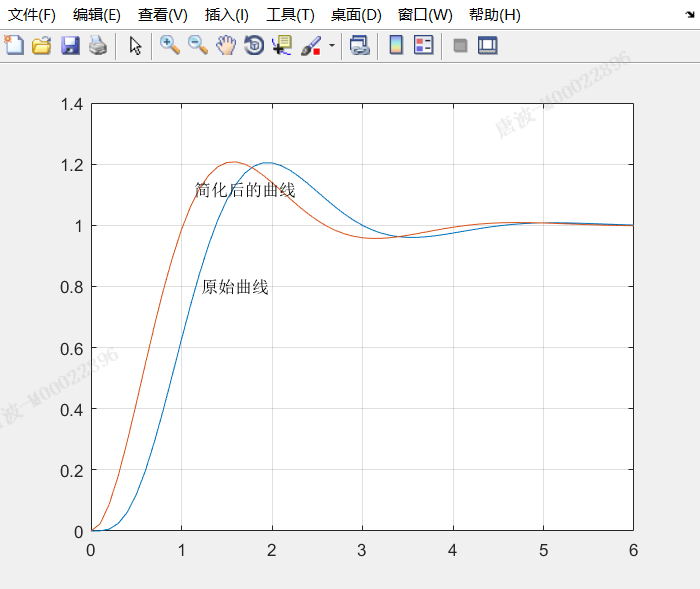
plot(t,y0,t,y1);
grid;
gtext('原始曲线');
gtext('简化后的曲线');

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wBR412Sa-1658734634920)(https://raw.githubusercontent.com/yumo2021/PicGo1/main/20220608193659.png)]

num=500;
den=conv([1,10,50],[1,10]);
sys=tf(num,den);
pzmap(sys)
sys0=tf(50,[1,10,50]);
t=0:0.01:4
y=step(sys,t);
y0=step(sys0,t);
plot(t,y,t,y0);
grid

5.3稳定性分析

此书仅介绍经典提法：若系统在足够小的初始偏差作用下，其过度过程随时间的退役逐渐衰减并趋于零，即具有回复原平衡态的能力。

5.3.2稳定性的判据

稳定性的问题归结于系统闭环极点的求取，即闭环特征方程根的问题。由于高阶代数方程的根一般没有解析解，故只能用数值方法求取。其次直接求根法来分析系统稳定性，不易给出系统结构和参数与稳定性的关系，对系统的综合问题帮助不大，因此需要寻求不直接求解方程代数方程的方法来判断系统稳定性。就是所谓稳定性判据。常见的有劳斯判据和赫尔维茨判据。

1. 劳斯判据
2. 赫尔维茨判据

最后

以上就是内向含羞草为你收集整理的Simulink与控制系统仿真笔记05Simulink与控制系统仿真笔记055.时域分析法的全部内容，希望文章能够帮你解决Simulink与控制系统仿真笔记05Simulink与控制系统仿真笔记055.时域分析法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。