参考资料:OTFS-SCMA: A Downlink NOMA Scheme
for Massive Connectivity in High Mobility
Channels
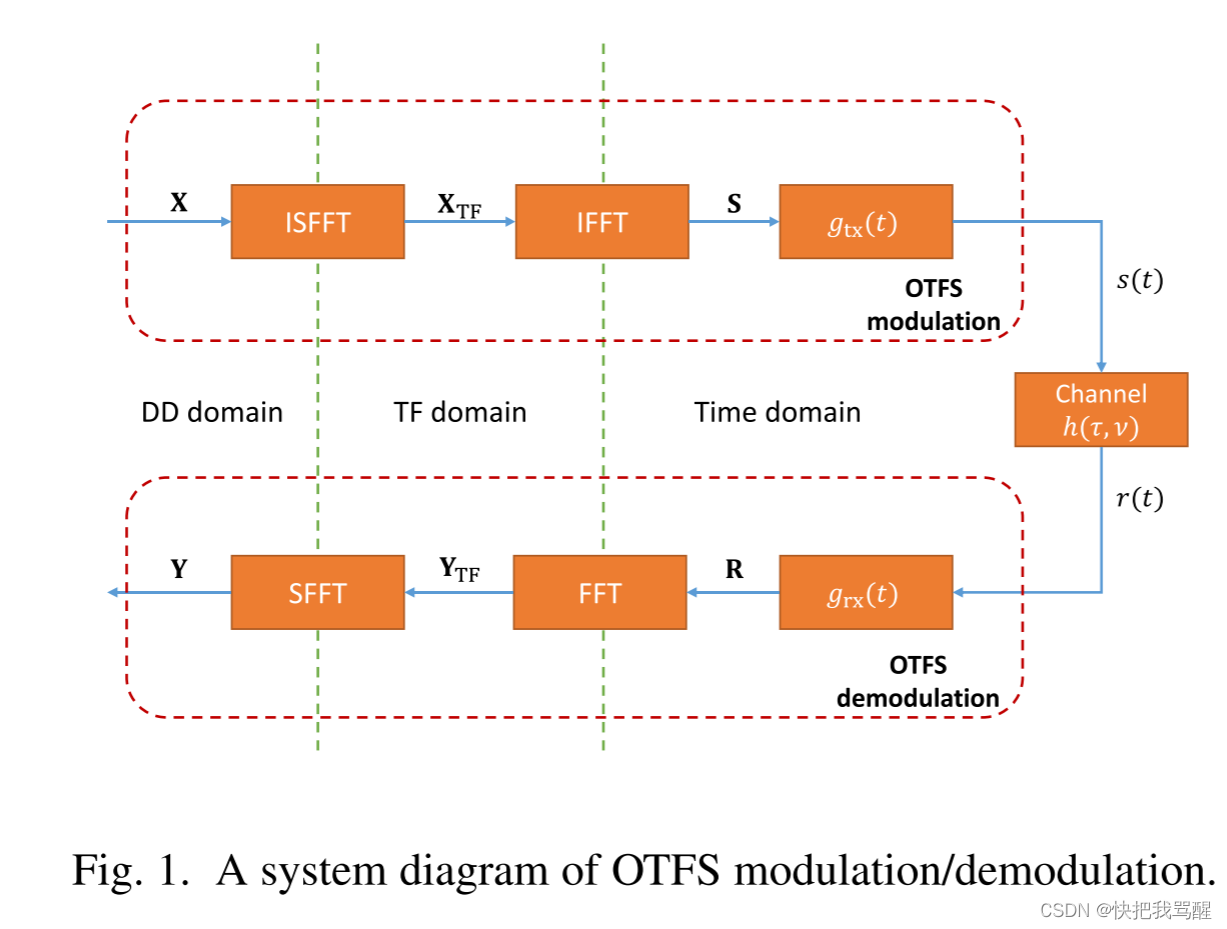
OTFS系统流程
X
[
m
,
n
]
X[m,n]
X[m,n]是DD时延多普勒域
Γ
=
{
(
m
M
Δ
f
,
n
N
T
)
,
m
=
0
,
…
,
M
−
1
,
n
=
0
,
…
,
N
−
1
}
Gamma=left{left(frac{m}{M Delta f}, frac{n}{N T}right), m=0, ldots, M-1, n=0, ldots, N-1right}
Γ={(MΔfm,NTn),m=0,…,M−1,n=0,…,N−1}中的符号,
M
Δ
f
M Delta f
MΔf是OTFS帧的带宽,
N
T
NT
NT is the OTFS frame duration with
∆
f
=
1
/
T
∆f = 1/T
∆f=1/T.
The OTFS transmitter first maps the symbols
X
[
m
,
n
]
X[m,n]
X[m,n] to the TF domain grid
Π
=
{
(
l
Δ
f
,
k
T
)
,
l
=
0
,
…
,
M
−
1
Pi={(l Delta f,kT),l=0,ldots,M-1
Π={(lΔf,kT),l=0,…,M−1
k
=
0
,
…
,
N
−
1
}
k = 0,ldots,N−1}
k=0,…,N−1} via inverse finite symplectic Fourier transform (ISFFT) as [5] as follows:
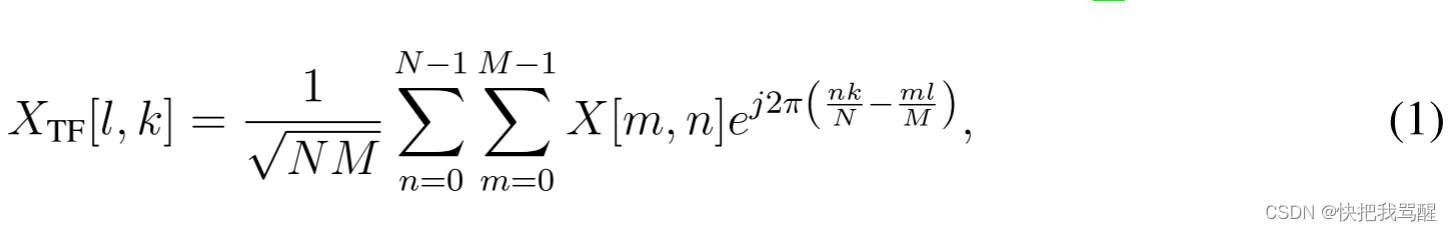
其中
X
T
F
[
l
,
k
]
X_{TF}[l,k]
XTF[l,k]表示TF(TimeFreq)域发射的符号。时域信号
s
(
t
)
s(t)
s(t)因此可以由传统OFDM调制器产生,即,TF域符号
X
T
F
[
l
,
k
]
X_{TF}[l,k]
XTF[l,k]接着由具有持续时间T的发射器整形脉冲
g
t
x
(
t
)
g_{tx}(t)
gtx(t)的常规OFDM调制器转换为连续时间波形
s
(
t
)
s(t)
s(t),即
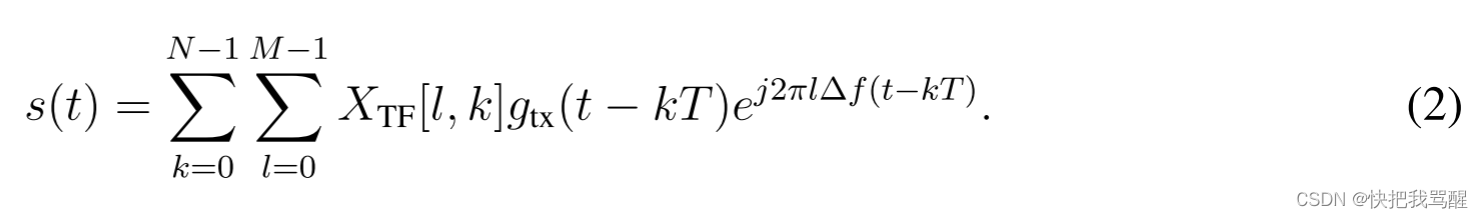
信号
s
(
t
)
s(t)
s(t)在时变无线信道上传输,该时变无线信道由具有延迟
τ
τ
τ和多普勒
ν
ν
ν的脉冲响应
h
(
τ
,
ν
)
h(τ,ν)
h(τ,ν)表征,由下式给出
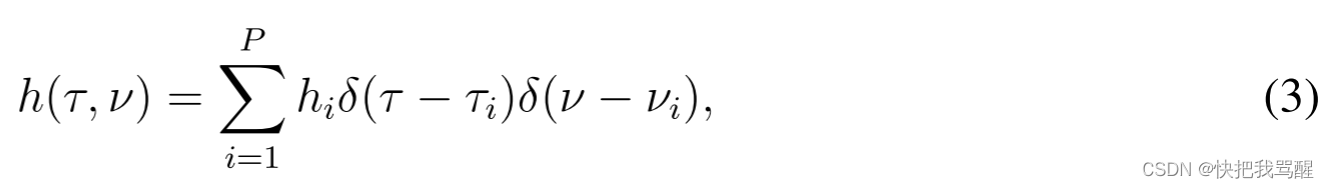
其中
P
P
P表示路径数,
h
i
、
τ
i
h_i、τ_i
hi、τi和
ν
i
ν_i
νi分别表示第
i
i
i条路径的路径增益、延迟和多普勒频移。注意,
τ
i
τ_i
τi和
ν
i
ν_i
νi取决于第i条路径的延迟和多普勒指数,由[36]给出。
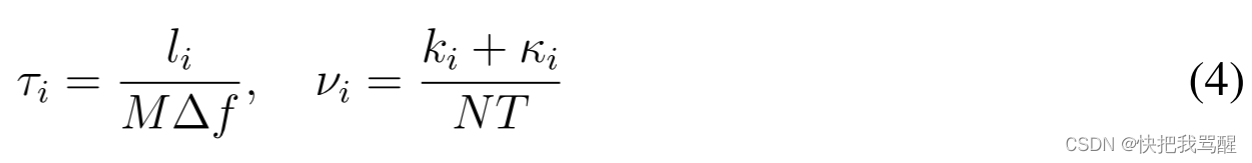
其中整数
l
i
、
k
i
l_i、k_i
li、ki和分数多普勒项
−
1
/
2
≤
κ
i
≤
1
/
2
−1/2 ≤ κ_i ≤ 1/2
−1/2≤κi≤1/2。在接收机侧,接收信号
r
(
t
)
r(t)
r(t)由下式给出:
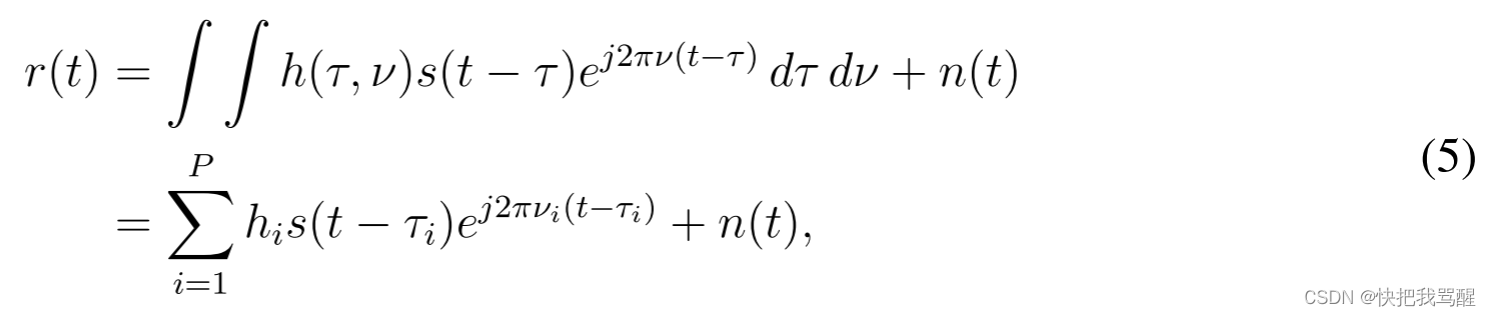
其中
n
(
t
)
n(t)
n(t)是具有单侧功率谱密度
N
0
N_0
N0的加性高斯白噪声(AWGN)信号。OTFS接收机在接收到
r
(
t
)
r(t)
r(t)之后,利用匹配滤波器
g
r
x
(
t
)
g_{rx}(t)
grx(t)将时域信号转换为TF域符号
Y
T
F
[
l
,
k
]
Y_{TF}[l,k]
YTF[l,k],即[5]。
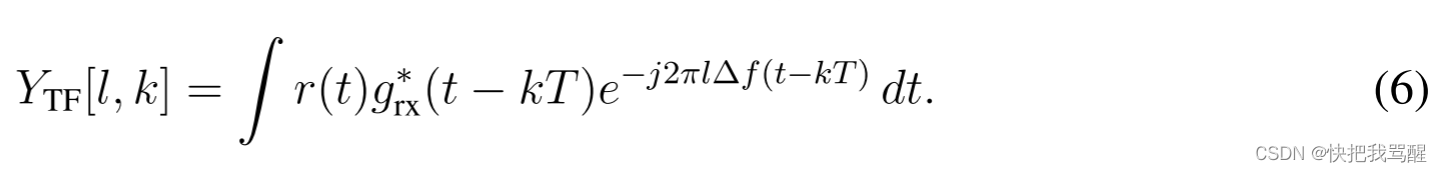
最后,DD域接收符号
Y
[
m
,
n
]
Y[m,n]
Y[m,n]可以通过对
Y
T
F
[
l
,
k
]
Y_{TF}[l,k]
YTF[l,k]执行SFFT来获得,如下
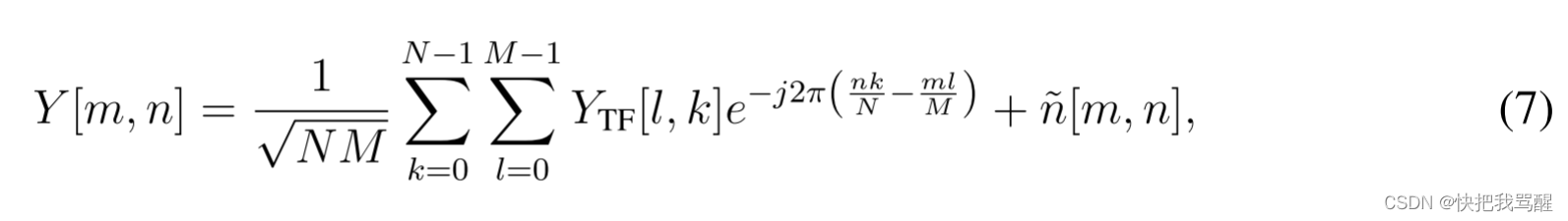
其中
n
[
m
,
n
]
n[m,n]
n[m,n]表示DD域中的对应AWGN采样。
将OTFS系统流程向量化
其次,我们可以将不同领域的输入输出关系改写成向量化的形式,以简化后续的推导。在本文中,我们遵循与文献[28]中OTFS系统的矩阵/向量表示相同的符号。设
X
,
Y
∈
C
M
×
N
X,Y ∈ mathbb{C}^{M×N}
X,Y∈CM×N为发送和接收的DD域符号矩阵,TF域对应的符号矩阵分别记为
X
T
F
∈
C
M
×
N
X_{TF} ∈ mathbb{C}^{M×N}
XTF∈CM×N和
Y
T
F
∈
C
M
×
N
Y_{TF} ∈ mathbb{C}^{M×N}
YTF∈CM×N。对于时域,发射符号矩阵和接收符号矩阵分别表示为
S
∈
C
M
×
N
S ∈ mathbb{C}^{M×N}
S∈CM×N和
R
∈
C
M
×
N
R ∈ mathbb{C}^{M×N}
R∈CM×N。
设
F
M
F_M
FM和
F
N
F_N
FN是归一化的M点和N点离散傅里叶变换(DFT)矩阵。方程式(1)可以重新表述为

来自具有矩形脉冲的TF域采样的发射时域信号可重写为

因此,时域传输向量
S
∈
C
M
N
×
1
S ∈ mathbb{C}^{MN×1}
S∈CMN×1由下式给出:

其中
x
≜
vec
(
X
)
mathbf{x} triangleq operatorname{vec}(mathbf{X})
x≜vec(X)
考虑到减少的循环前缀帧格式,在接收器侧,在丢弃CP之后,我们可以通过以速率
f
s
=
M
∆
f
f_s = M∆f
fs=M∆f离散化时域接收信号来以矢量化形式重写(5),如[36]
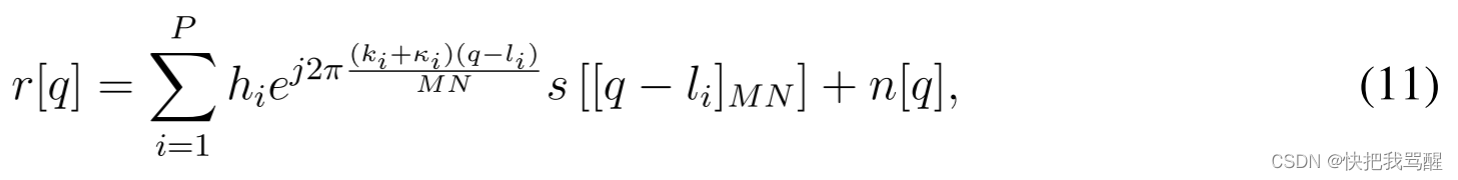
其中
[
⋅
]
M
N
[·]_{MN}
[⋅]MN表示mod-MN运算,
q
=
0
,
.
.
.
,
M
N
−
1
q = 0,...,MN − 1
q=0,...,MN−1。因此,向量形式的离散时域输入-输出关系可由下式给出:

其中,有效时域信道矩阵HT由下式给出:
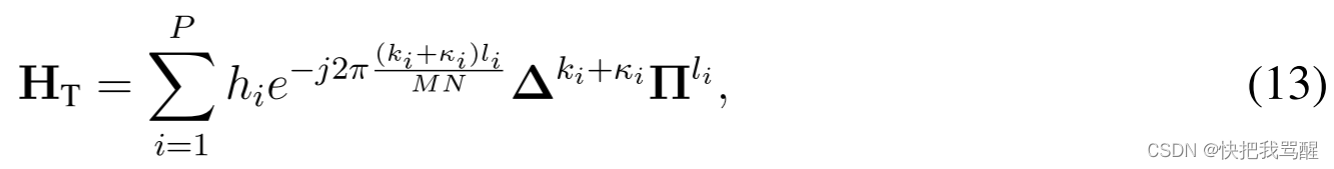
H
T
=
∑
i
=
1
P
h
i
e
−
j
2
π
(
k
i
+
κ
i
)
l
i
M
N
Δ
k
i
+
κ
i
Π
l
i
mathbf{H}_{mathrm{T}}=sum_{i=1}^{P} h_{i} e^{-j 2 pi frac{left(k_{i}+kappa_{i}right) l_{i}}{M N}} Delta^{k_{i}+kappa_{i}} boldsymbol{Pi}^{l_{i}}
HT=i=1∑Phie−j2πMN(ki+κi)liΔki+κiΠli
其中
Δ
=
diag
(
[
1
,
e
j
2
π
1
M
N
,
…
,
e
j
2
π
M
N
−
1
M
N
]
)
boldsymbol{Delta}=operatorname{diag}left(left[1, e^{j 2 pi frac{1}{M N}}, ldots, e^{j 2 pi frac{M N-1}{M N}}right]right)
Δ=diag([1,ej2πMN1,…,ej2πMNMN−1])是相位旋转矩阵,
Π
boldsymbol{Pi}
Π是置换矩阵(前向循环移位),由下式给出
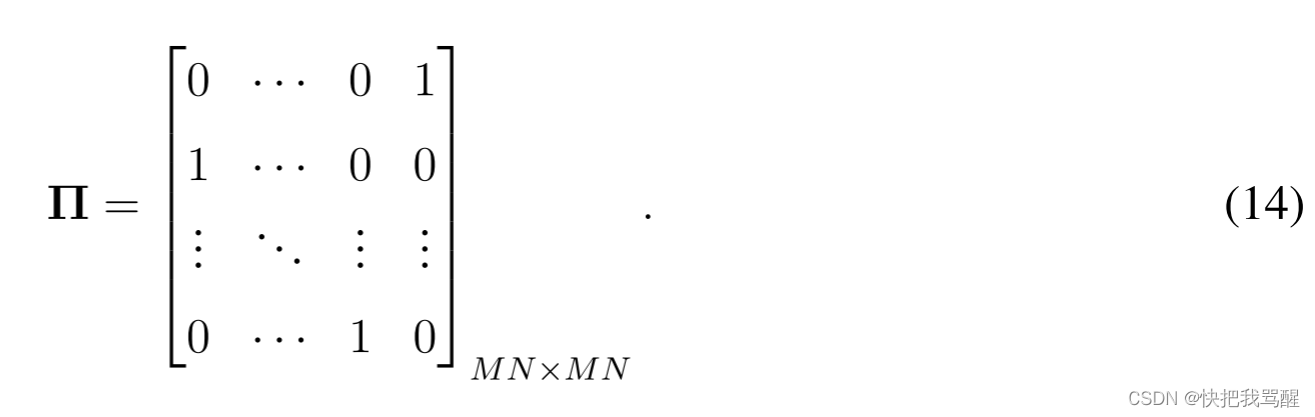
根据(6)-(10),并且通过假设矩形脉冲整形波形,DD域接收符号向量
y
≜
vec
(
Y
)
mathbf{y} triangleq operatorname{vec}(mathbf{Y})
y≜vec(Y)由下式给出
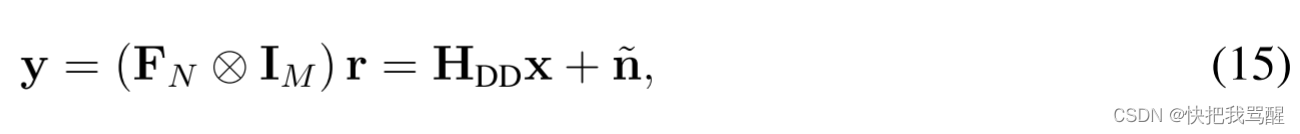
其中DD域有效信道矩阵
H
D
D
mathbf{H}_{DD}
HDD由下式给出
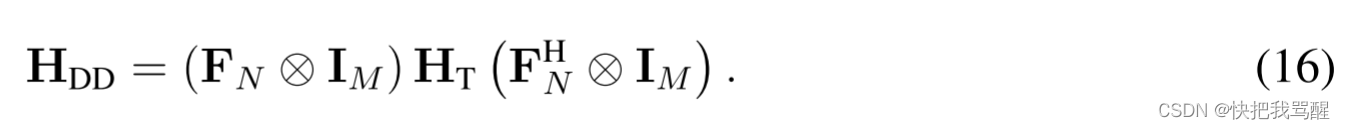
可以看出,在存在分数多普勒频移的情况下,(16)中的DD域中的有效信道矩阵
H
D
D
mathbf{H}_{DD}
HDD可能变得密集,而(13)中的时域有效信道矩阵
H
T
mathbf{H}_{T}
HT保持稀疏。特别地,在
H
T
mathbf{H}_{T}
HT的每一行和每一列中存在至多
l
m
a
x
l_{max}
lmax个非零条目。
H
T
mathbf{H}_{T}
HT的稀疏性促使我们在时域中执行均衡。而且,一旦信道在时域中被均衡,我们就能够在DD域中执行低复杂度的近似最大似然(ML)检测。
SCMA的一些相关博客
转自https://blog.csdn.net/guolianggsta/article/details/127486764
SCMA就属于NOMA的一种关键技术
F-OFDM解决了业务灵活性的问题,还得考虑如何利用有限的频谱,提高资源利用率,容纳更多用户,提升更高吞吐率。有限空间的火车里,如何装更多的人?要提高资源利用率,哪些域的资源能够进一步复用?我们想到了LTE时代没有重用的码域资源。SCMA技术,引入稀疏码本,通过码域的多址实现了频谱效率的3倍提升,相当于有限的火车座位上,坐了更多的用户。如同4个同类型的并排座位,坐6个人进去挤一挤,这就实现了1.5倍的频谱效率提升。
SCMA的第一个关键技术就是低密度扩频。如图9-39所示,SCMA的原理就是把单个子载波的用户数据扩频到4个子载波上,然后6个用户共享这4个子载波。之所以叫低密度扩频,是因为一个用户的数据只占用了其中2个子载波(图中有颜色的格子),另外2个子载波是空的(图中白色的格子)。这也是SCMA中Sparse(稀疏)的由来。如果不稀疏,就是在全载波上扩频,那同一个子载波上就有6个用户的数据,或者一个用户的数据占用4个子载波,冲突太厉害,无法准确解调用户的数据。
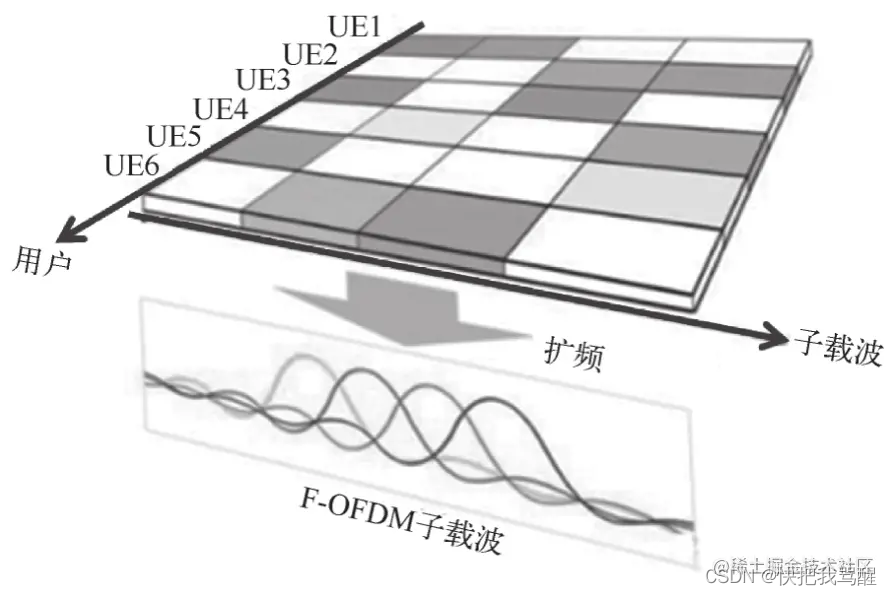
图9-39 SCMA原理
4个座位(子载波)坐了6个用户之后,乘客之间就不严格正交了。这是因为每个座位有两个乘客了,没法再通过座位号(子载波)来区分乘客了。单一子载波上还是有3个用户的数据冲突,怎么把一个子载波上的多个用户数据解调出来?
这就需要SCMA第二个关键技术——高维调制。因为传统的IQ调制只有两维:幅度和相位,高维体现在哪里?如果两个乘客挤在一个座位上,没法再用座位号来区分乘客,但如果给这些乘客贴上不同颜色的标签,结合座位号,还是可以把乘客给区分出来。稀疏码本就是贴在不同用户上的标签,相当于乘客身上不同颜色的标签。高维调制技术是指每个用户的数据在幅值和相位的基础上,使用系统分配的稀疏码本再进行调制,接收端又知道每个用户的码本,这样就可以在不正交的情况下,把不同用户的数据解调出来。
SCMA在使用相同频谱的情况下,通过引入码域的多址,大大提升了频谱效率,通过使用数量更多的载波组,并调整单用户承载数据的子载波数(即稀疏度),频谱效率可以提升3倍以上。
转自https://blog.csdn.net/ZhongGuoRenMei/article/details/117527694
SCMA(Sparse Code Multiple Access,稀疏码分多址接入)技术是由华为公司所提出的第二个第五代移动通信网络全新空口核心技术,引入稀疏编码对照簿,通过实现多个用户在码域的多址接入来实现无线频谱资源利用效率的提升。SCMA码本设计是其核心,码本设计主要是两大部分:1.低密度扩频;2.高维QAM调制。将这两种技术结合,通过共轭、置换、相位旋转等操作选出具有最佳性能的码本集合,不同用户采用不同的码本进行信息传输。码本具有稀疏性是由于采用了低密度扩频方式,从而实现更有效的用户资源分配及更高的频谱利用;码本所采用的高维调制通过幅度和相位调制将星座点的欧式距离拉得更远,保证多用户占有资源的情况下利于接收端解调并且保证非正交复用用户之间的抗干扰能力。下面通过图片展示。
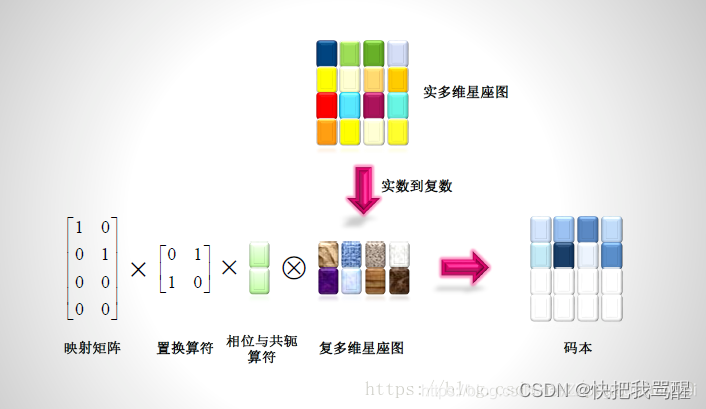
低密度扩频技术
举例而言,现实生活中,如果一排位置仅有4个座位,但有6个人要同时坐上去,怎么办?解决的办法是这6个人挤着坐这4个座位。同理,在未来的第五代移动通信系统之中,如果某一组子载波之中仅有4个子载波,但是却有6个用户由于同时对某种业务服务有需求而要接入到系统之中,怎么办?低密度扩频技术就“应运而生”了:如图3所示,把单个子载波的用户数据扩频到4个子载波上,然后,6个用户共享这4个子载波。可见,之所以被称之为“低密度扩频”,是因为用户数据仅仅只占用了其中的两个子载波(图3中有颜色的格子部分),而另外两个子载波则是空载的(图3中的白色格子)——于是,这就相当于6个乘客同时挤着坐4个座位——另外,这也是SCMA(Sparse Code Multiple Access,稀疏码分多址接入)中“Sparse(稀疏)”的来由。
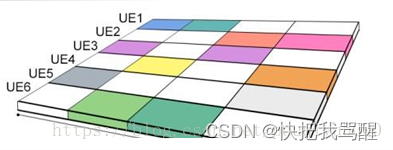
4个子载波搭载6个用户示意图
高维调制技术
传统的调制技术之中,仅涉及幅度与相位这两个维度。那么,在多维/高维调制技术之中,除了“幅度”与“相位”,多出来的是什么维度的呢?其实,多维/高维调制技术之中所调制的对象仍然还是相位和幅度,但是最终却使得多个接入用户的星座点之间的欧氏距离拉得更远,多用户解调与抗干扰性能由此就可以大大地增强。每个用户的数据都使用系统所统一分配的稀疏编码对照簿进行多维/高维调制,而系统又知道每个用户的码本,于是,就可以在相关的各个子载波彼此之间不相互正交的情况下,把不同用户的数据最终解调出来。作为与现实生活之中相关场景的对比,上述这种理念可以理解为:虽然无法再用座位号来区分乘客,但是可以给这些乘客贴上不同颜色的标签,然后结合座位号,还是能够把乘客区分出来。

大家可能很难理解为什么明明就只有两维调制的相位和幅度怎么就拉开欧式距离呢?以图4为例,图4是一个高维想象图,我们可以看见在二维图时,小狗图像密集在圆内,而在三维图形中,方体内的球体的小狗被拉向对角处,在机器学习中,这被称之为维度灾难。我们可以在脑海中,构建出这样一幅景象:本来很密集的星座图(2维),通过提升维度,它们之间的相互距离不断拉大,类似于上图中小狗与小狗之间的距离,这就很容易理解,上面的话了,所调制的对象不变,但是由于提升维度,造成欧式距离增大,从而更容易分离出来,也便于后面的多用户检测了,perfect!
今天主要是给大家科普一下5G的多址技术,综合使用SCMA的两大关键技术(低密度扩频技术与多维/高维调制技术),SCMA(Sparse Code Multiple Access,稀疏码分多址接入)技术可使得多个用户在同时使用相同无线频谱资源的情况下,引入码域的多址,大大提升无线频谱资源的利用效率,而且通过使用数量更多的子载波组(对应服务组),并调整稀疏度(多个子载波组中,单用户承载数据的子载波数),来进一步地提升无线频谱资源的利用效率。
SCMA的实现基于两步:
1.实现码本资源到物理频域资源映射的映射矩阵(matrix mapping);
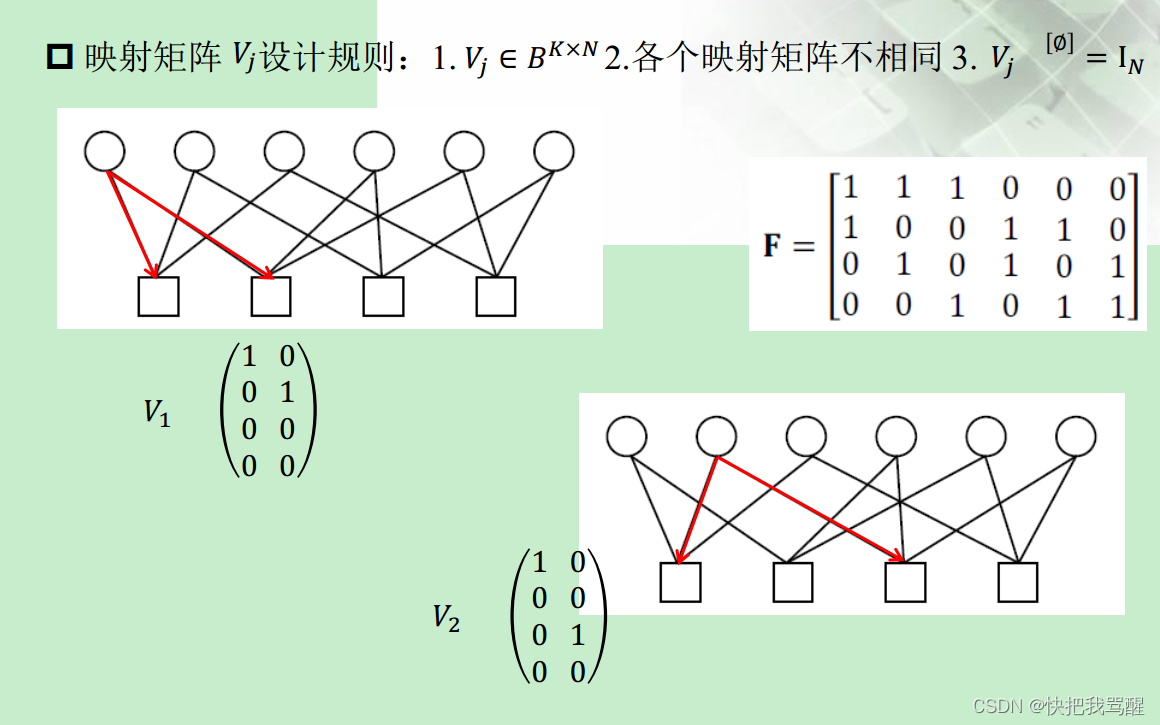
2.实现二进制比特流到码本映射的复数域星座图(complex domain constellation design);
(b1,b2)-----复数域星座映射(二维)------>(x1,x2,x3,x4)------一个码字到两个物理资源块的映射(每个资源块实现一个复信号的传输)------->f1:x1+jx2 f2:x3+jx4
上述过程实现了一个码字在两个物理资源块上的传输。
而在普通的OFDM中,一个(b1,b2)-----星座映射------>(x1,x2)------映射到一个物理资源块(每个资源块实现一个复信号的传输)------->f1:x1+jx2
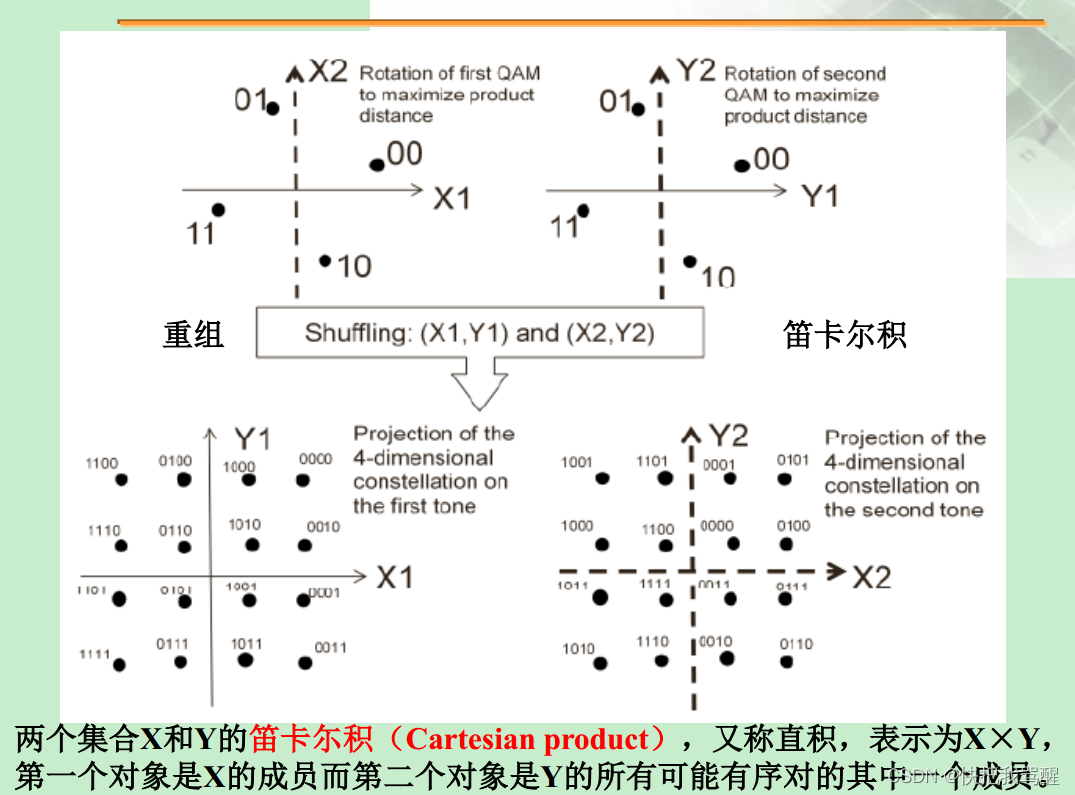

摘自博客
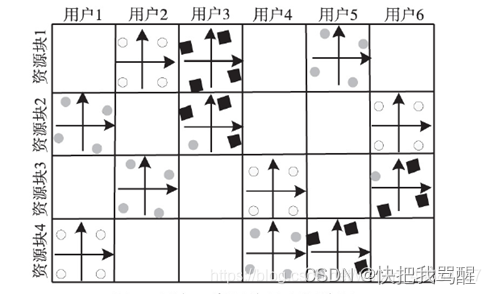
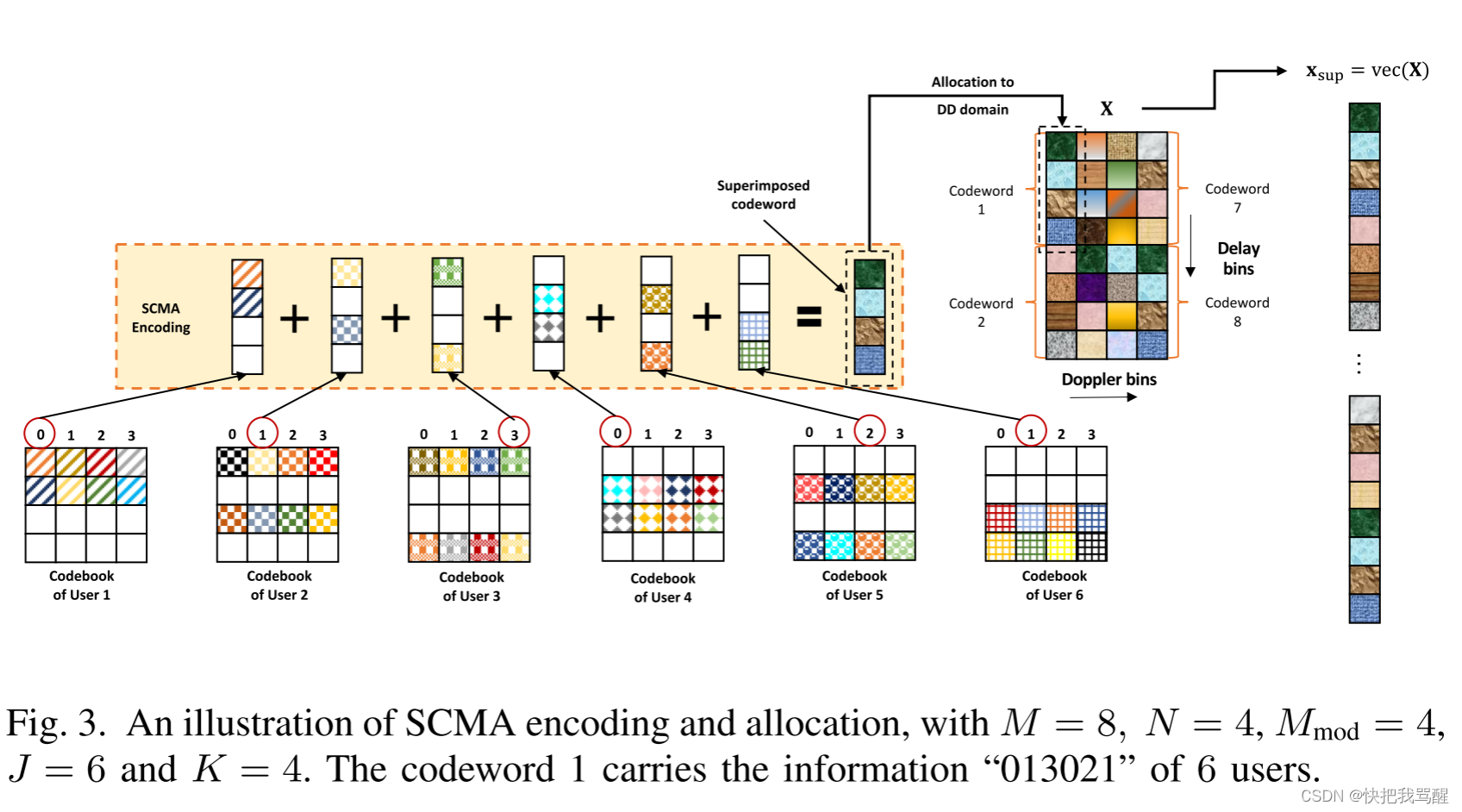
SCMA编码原理如图1所示,这里以六个用户在四个资源块上传输,每个用户采用4点星座图进行调制为例来说明。每个用户对应一个独一无二的码本,每个码本是一个4×4的复数矩阵,其中矩阵的行表示资源块,矩阵的列表示码字。每个用户每次传输2 bit信息,包含四种可能的值,分别对应四个码字,假设用户发送的二进制比特为00-11时分别对应用户码本的第1~4列。
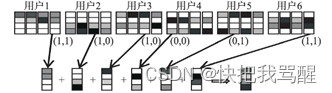
图1表示六个用户同时发送信息,用户1~6分别传输11、10、10、00、01、11,各用户对应码本的第4、3、3、1、2、4列码字被挑选出来,叠加在四个资源块上传输。对于每一个码字而言,包含零项和非零项,零项表示用户在该资源块上不传输信号,非零项表示用户在该资源块上传输信号,且信号的强度为非零项的值。为了表示的方便,本文采用F矩阵来表示这样一种结构,图1对应的F矩阵为:
F 4 × 6 = [ 1 0 1 0 1 0 1 0 0 1 0 1 0 1 1 0 0 1 0 1 0 1 1 0 ] mathrm{F}_{4 times 6}=left[begin{array}{cccccc} 1 & 0 & 1 & 0 & 1 & 0 \ 1 & 0 & 0 & 1 & 0 & 1 \ 0 & 1 & 1 & 0 & 0 & 1 \ 0 & 1 & 0 & 1 & 1 & 0 end{array}right] F4×6= 110000111010010110010110

对应结构图如下所示
F 4 × 6 = [ 0 1 1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1 1 0 0 1 1 0 ] mathrm{F}_{4 times 6}=left[begin{array}{cccccc} 0 & 1 & 1 & 0 & 1 & 0 \ 1 & 0 & 1 & 0 & 0 & 1 \ 0 & 1 & 0 & 1 & 0 & 1 \ 1& 0 & 0 & 1 & 1 & 0 end{array}right] F4×6= 010110101100001110010110
SCMA
考虑下行链路 K × J K×J K×JSCMA系统,其中 J J J个用户在 K K K个资源节点上通信以进行多址接入。典型地, J > K J>K J>K指示并发通信的用户的数目大于正交资源的总数,并且过载因子由 λ = J / K > 1 λ = J/K>1 λ=J/K>1定义。
每个用户被预先分配一个码本
X
j
∈
C
K
×
M
m
o
d
mathcal{X}_{j} in mathbb{C}^{K times M_{bmod }}
Xj∈CK×Mmod,并且
j
∈
1
,
2
…
,
J
j ∈ {1,2ldots,J}
j∈1,2…,J,其由维数为
K
K
K的
M
m
o
d
M_{mod}
Mmod个码字组成。我们考虑功率预算使得
T
r
(
X
j
X
j
H
)
/
M
m
o
d
=
1
Tr(mathcal{X}_{j} mathcal{X}_{j}^{H} )/M_{mod} = 1
Tr(XjXjH)/Mmod=1。用户
j
j
j的SCMA编码器从码本
X
j
X_j
Xj中选择对应于具有
l
o
g
2
(
M
m
o
d
)
log_2(M_{mod})
log2(Mmod)比特的输入二进制消息
b
j
b_j
bj的码字。令用户
j
j
j的码字为
X
j
=
[
X
j
,
1
,
X
j
,
2
,
…
,
X
j
,
K
]
T
∈
C
K
×
1
X_j = [X_{j,1},X_{j,2},ldots,X_{j,K}]^T ∈ mathbb{C}^{K×1}
Xj=[Xj,1,Xj,2,…,Xj,K]T∈CK×1.然后将
J
J
J个用户的码字叠加在
K
K
K个资源节点上,即,

其中
x
S
C
M
A
∈
C
K
×
1
x_{SCMA} ∈ mathbb{C}^{K×1}
xSCMA∈CK×1被称为叠加码字,可以被视为一个大小为
M
m
o
d
J
M^J_{mod}
MmodJ的大叠加星座中的点。对于SCMA,码本是稀疏的,即
X
j
mathcal{X}_{j}
Xj,
∀
j
forall j
∀j中的每个码字由
K
−
d
v
K−d_v
K−dv个零和
d
v
d_v
dv个非零元素组成,每个资源节点携带
d
c
d_c
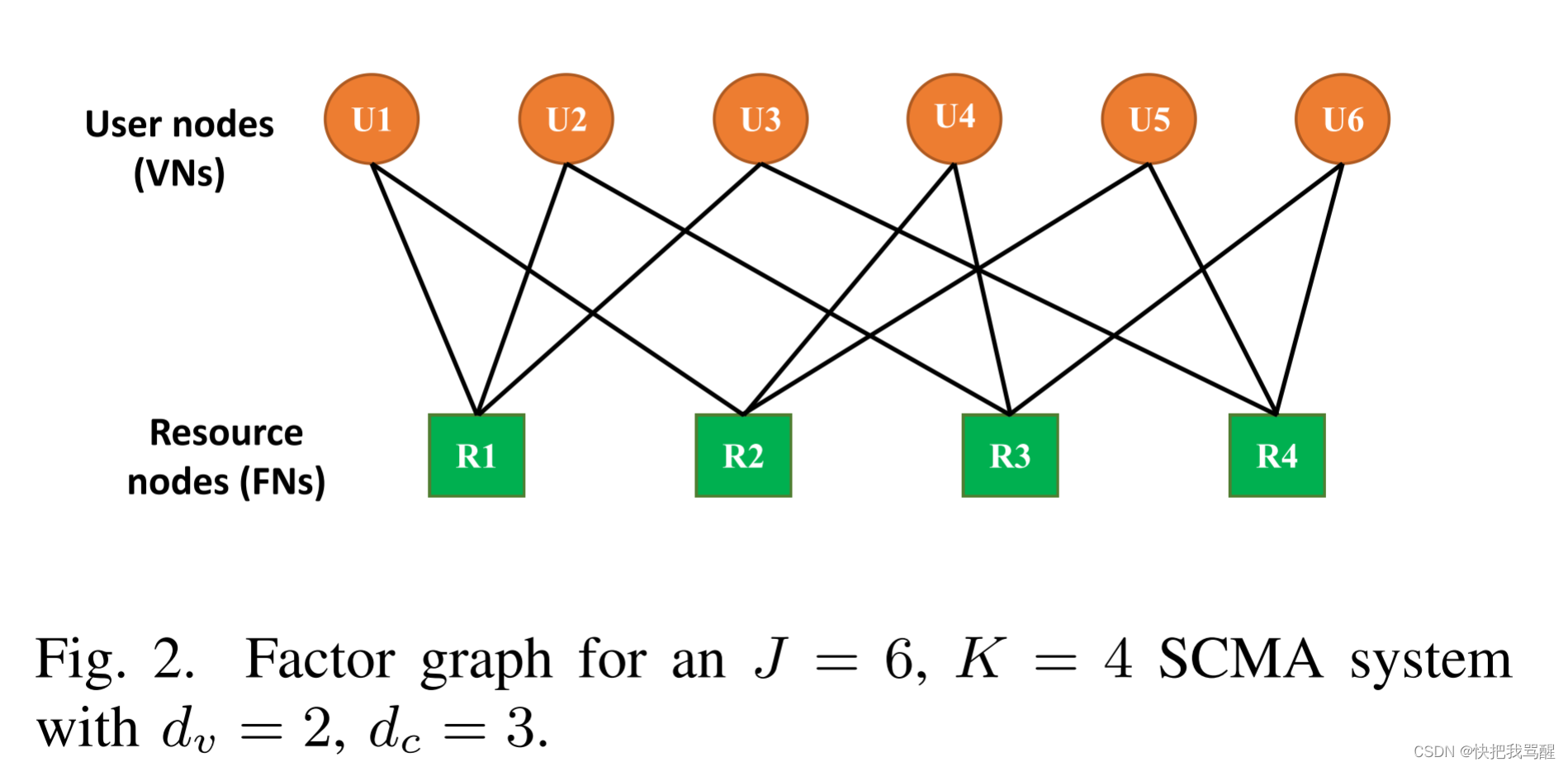
dc个用户的符号。用户节点(VN)和资源节点(FN)之间的关系可以由因子图表示,如图2所示,其中
J
=
6
J = 6
J=6,
K
=
4
K = 4
K=4,
d
v
=
2
d_v = 2
dv=2,以及
d
c
=
3
d_c = 3
dc=3。当且仅当第j个用户节点占用第k个资源节点,一个边被分配到两个节点之间,即,
X
j
,
k
≠
0
X_{j,k} ne 0
Xj,k=0。
因子图的替代表示是指示符矩阵,其中每行指示特定资源节点,并且该行中的所有非零条目对应于该资源节点上的活动用户。具体而言,图2所示因子图的指标矩阵由下式给出:
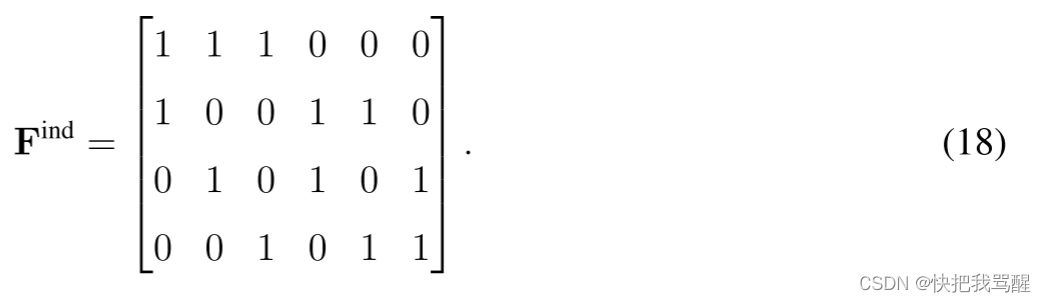
给定一个信道矩阵
H
D
D
H_{DD}
HDD,下行SCMA系统接收到的信号
y
S
C
M
A
y_{SCMA}
ySCMA可以表示为:
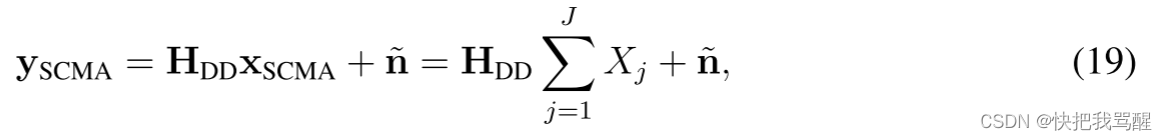
其中
n
~
tilde{n}
n~是DD域中对应的AWGN采样向量。
基于SCMA因子图,MPA解码器可用于解码SCMA码字[10]。
OTFS grid中SCMA码字的分配
不失一般性,我们认为SCMA码字在DD域平面上沿着延迟方向以大小为 K × 1 K×1 K×1的块来分配。值得一提的是所提出的OTFS-SCMA检测器也可以与其他分配方案一起工作。
因此,OTFS帧包括
⌊
M
N
K
⌋
leftlfloorfrac{M N}{K}rightrfloor
⌊KMN⌋个SCMA码字。第
j
j
j个用户发送的DD域符号向量可以表示为(下面假设MN正好是K的倍数):
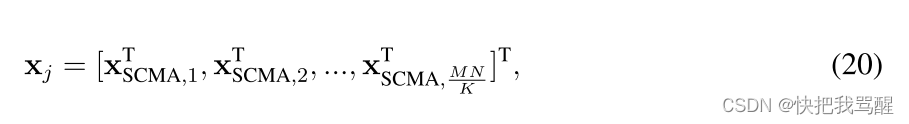
其中
x
S
C
M
A
,
i
x_{SCMA,i}
xSCMA,i表示用户j的第
i
i
i个SCMA码字。然后,发射机将DD域中所有用户的符号向量叠加,并构造对应的叠加码字向量
x
s
u
p
mathbf{x}_{sup}
xsup,即:

对于下行链路用户
j
j
j,接收到的DD域符号向量可以建模为

其中下标
j
j
j用于区分不同用户的信道和接收信号。类似地,我们可以获得用户
j
j
j在时域中的发送向量和接收向量,即
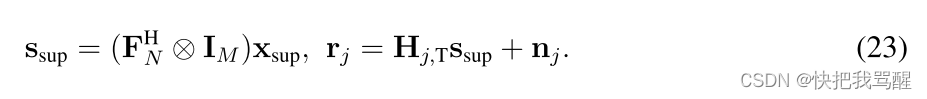
图3示出了DD域中的SCMA编码和分配。为了便于说明,我们仅示出
M
=
8
M = 8
M=8、
N
=
4
N = 4
N=4的情形。然而,由于SCMA码字是以块为单位分配的,因此所提出的算法可以扩展到更大的OTFS-SCMA系统。
带跨域检测器的OTSF-SCMA联合译码
在本节中,我们提出了一种如图5所示的单层结构的跨域OTFS-SCMA检测器,该检测器在下行用户本地执行。特别地,我们假设每个资源节点上的归一化叠加码字独立地相同分布(i.i.d.),即 E ( x sup x sup H ) = I M N mathbb{E}left(mathbf{x}_{text {sup }} mathbf{x}_{text {sup }}^{mathrm{H}}right)=mathbf{I}_{M N} E(xsup xsup H)=IMN。
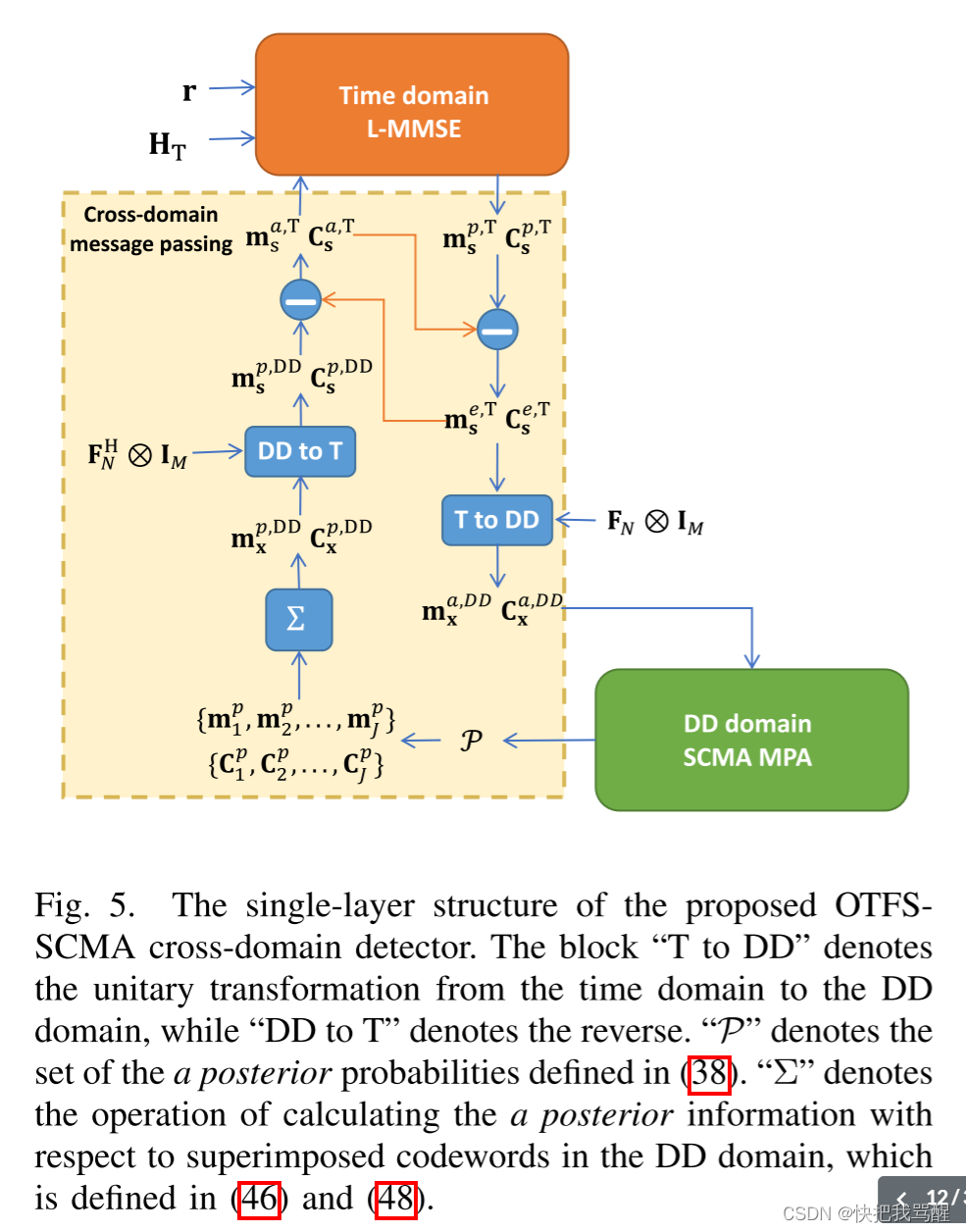
图4示出了通过具有1000帧的蒙特卡罗模拟得到的
E
(
x
sup
x
sup
H
)
mathbb{E}left(mathbf{x}_{text {sup }} mathbf{x}_{text {sup }}^{mathrm{H}}right)
E(xsup xsup H)的示例,表明该假设在很大程度上是有效的。在酉变换的基础上,
S
S
U
P
S_{SUP}
SSUP的i.i.d.假设也是适用的,即,
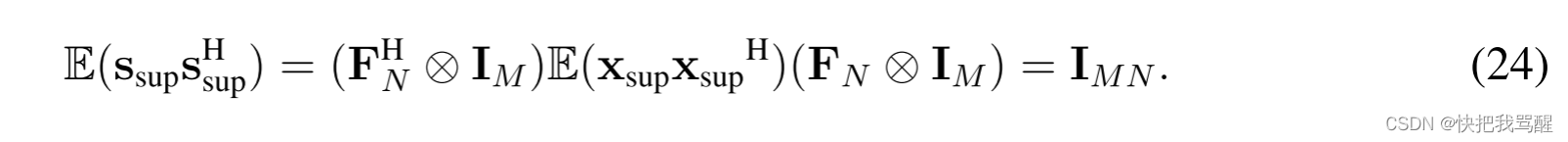
此外,由于ISFFT的扩展效应,我们假设
S
S
U
P
S_{SUP}
SSUP中的entries是高斯变量。
受OAMP [32],[37]误差正交性原理的启发,我们设计了一种由时域线性估计器(LE)和DD域非线性估计器(NLE)通过酉变换组成的跨域OTFS-SCMA检测器。为了满足误差的正交性,我们开发了一个跨域消息传递算法,如图5中黄色区域所示。从正交LE和NLE的观点来看,所提出的跨域检测器也可以在图6中示出。图6中的NLE和正交NLE分别用 ϕ ^ ( x ) hat{phi}(x) ϕ^(x)和 ϕ ( x ) phi(x) ϕ(x)表示,LE和正交LE分别用 γ ^ ( x ) hat{gamma}(x) γ^(x)和 γ ( x ) gamma(x) γ(x)表示。因此,跨域OTFS-SCMA检测器可以被写为
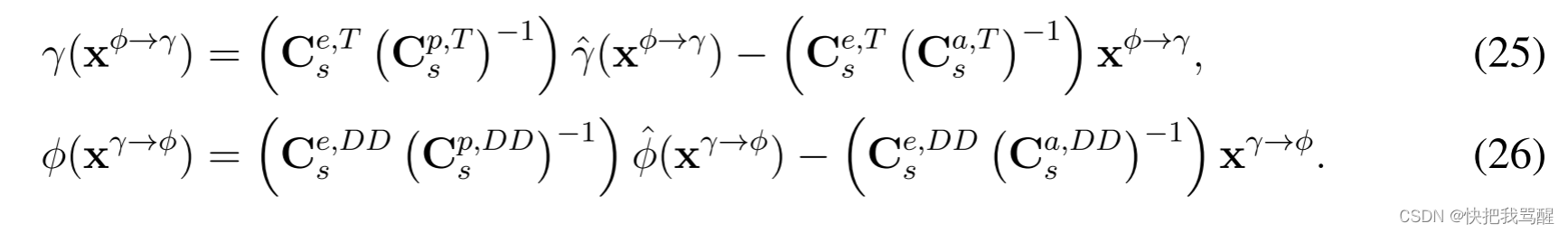
我们可以观察到,上述迭代过程实际上是一种期望传播(EP)。此外,根据[37],当采用局部最优原型时,EP和OAMP是等效的,例如:LMMSE估计器和SCMA MPA解码器。因此,在跨域消息传递的帮助下,时域LMMSE和DD域SCMA MPA解码器之间的误差是正交的,从而在迭代解码中产生增强的收敛。注意,所提出的基于误差正交性的OTFS-SCMA迭代检测器与基于turbo的迭代检测器根本不同,例如,基于turbo的LDPC SCMA检测器[38]和联合极化SCMA检测器[39],其要求每个局部估计器的独立输入-输出误差。此外,该方法利用酉变换代替了基于turbo的检测器中的传统的交织器。
最后
以上就是过时月光最近收集整理的关于OTFS-SCMA学习笔记OTFS系统流程将OTFS系统流程向量化SCMA的一些相关博客SCMAOTFS grid中SCMA码字的分配带跨域检测器的OTSF-SCMA联合译码的全部内容,更多相关OTFS-SCMA学习笔记OTFS系统流程将OTFS系统流程向量化SCMA的一些相关博客SCMAOTFS内容请搜索靠谱客的其他文章。








发表评论 取消回复