信息熵的计算公式_信息熵、条件熵、联合熵、互信息、相对熵、交叉熵

点击上方“机器学习与统计学”，选择“置顶”公众号

重磅干货，第一时间送达

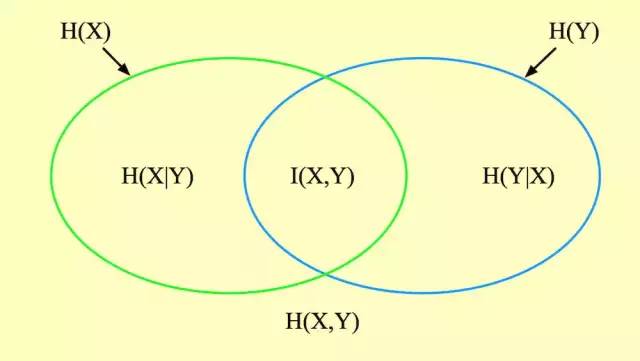
信息熵、联合熵、条件熵、互信息的关系

1、信息量

信息量是通过概率来定义的：如果一件事情的概率很低，那么它的信息量就很大；反之，如果一件事情的概率很高，它的信息量就很低。简而言之，概率小的事件信息量大，因此信息量可以定义如下：

下面解释为什么要取倒数再去对数。

(1)先取倒数： 这件事表示：“信息量”和“概率”呈反比；

(2)在取对数： 取对数是为了将区间 映射到 。

再总结一下：

2、信息熵

信息熵是信息量的数学期望。理解了信息量，信息熵的定义式便不难理解。定义如下：

• 熵越小表示越“纯”，决策树算法在进行特征选择时的其中标准之一就是选择使得通过该特征分类以后的类的熵最小；

• 上面是熵越小越好，而有的时候，我们需要熵越大越好，简单来说就是“鸡蛋不要放在一个篮子里”(见吴军《数学之美》)，最大熵原理就是这样，这部分内容可以参考李航《统计机器学习》逻辑回归模型相关部分。

3、条件熵

条件熵的定义为：在 给定的条件下， 的条件概率分布的熵对 的数学期望。

条件熵一定要记住下面的这个定义式，其它的式子都可以由信息熵和条件熵的定义式得出。

理解条件熵可以使用决策树进行特征选择的例子：我们期望选择的特征要能将数据的标签尽可能分得比较“纯”一些，特征将数据的标签分得“纯”，则熵就小，信息增益就大。

因为

条件熵可以变形成如下：

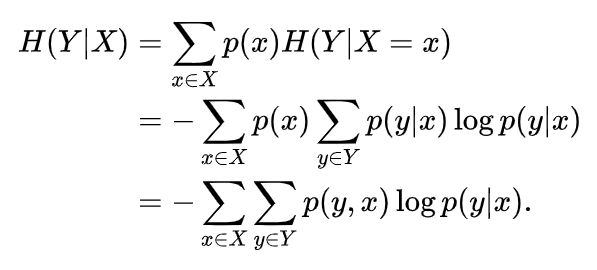
说明：有些教材直接把最后一步

定义成条件熵，其实是一个意思，我个人觉得

这种定义式更好理解，而这个定义式可以参考李航《统计学习方法》P61 ，并不难记忆，其实条件熵就是“被特征分割以后的信息熵的加权平均”。

4、联合熵

两个变量 和 的联合熵的表达式：

5、互信息

根据信息熵、条件熵的定义式，可以计算信息熵与条件熵之差：

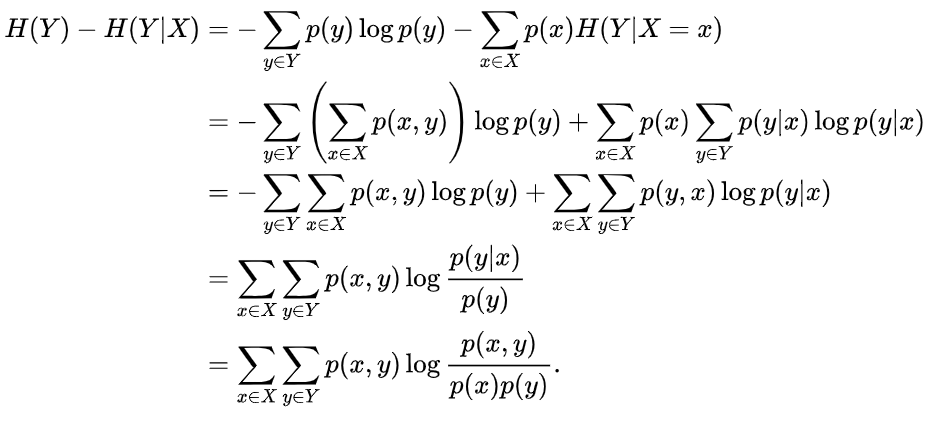
同理

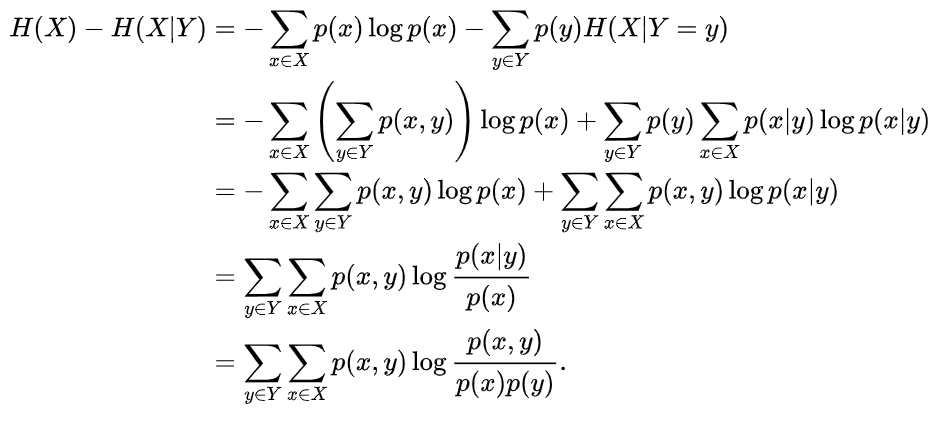
因此：定义互信息：

即：

互信息也被称为信息增益。用下面这张图很容易明白他们的关系。

信息熵、联合熵、条件熵、互信息的关系

信息熵：左边的椭圆代表 ，右边的椭圆代表 。互信息(信息增益)：是信息熵的交集，即中间重合的部分就是 。联合熵：是信息熵的并集，两个椭圆的并就是 。条件熵：是差集。左边的椭圆去掉重合部分就是 ，右边的椭圆去掉重合部分就是 。

还可以看出：

5、相对熵

相对熵又称 KL 散度，如果我们对于同一个随机变量 有两个单独的概率分布 和 ，使用 KL 散度(Kullback-Leibler (KL) divergence)来衡量这两个分布的差异。差异越大则相对熵越大，差异越小则相对熵越小。

计算公式如下：

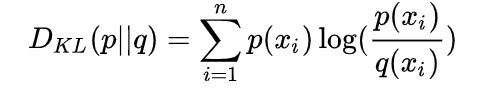
如何记忆：如果用 来描述样本，那么就非常完美(因为 认为是真实的情况)。而用 来描述样本，虽然可以大致描述，但是不是那么的完美，信息量不足，需要额外的一些“信息增量”才能达到和 一样完美的描述。如果我们的 通过反复训练，也能完美的描述样本，那么就不再需要额外的“信息增量”， 等价于 。即 和 的分布完全一致的时候，KL 散度的值等于 。

6、交叉熵

我是这样记忆交叉熵的定义的，通过逻辑回归的损失函数记忆交叉熵。 认为是类标，是独热编码(也可以认为是概率分布)，而 认为是逻辑回归预测的概率分布。

• 交叉熵是对数似然函数的相反数。对数似然的值我们希望它越大越好，交叉熵的值我们希望它越小越好。

结论：KL 散度 = 交叉熵 - 熵 。这一点从相对熵的定义式就可以导出。

这里

就是交叉熵的定义式。

相对熵与交叉熵的关系：

参考资料

1、一文搞懂交叉熵在机器学习中的使用，透彻理解交叉熵背后的直觉

地址：https://blog.csdn.net/tsyccnh/article/details/79163834

2、机器学习各种熵：从入门到全面掌握

地址：https://zhuanlan.zhihu.com/p/35423404

3、信息增益(互信息)非负性证明

地址：https://blog.csdn.net/MathThinker/article/details/48375523

4、如何通俗的解释交叉熵与相对熵?

地址： https://www.zhihu.com/question/41252833

5、相对熵(KL散度)

地址： https://blog.csdn.net/ACdreamers/article/details/44657745

6、KL(kullback-Leibler-devergence)散度(相对熵)非负性

地址：https://blog.csdn.net/KID_yuan/article/details/84800434

7、简单的交叉熵，你真的懂了吗？https://zhuanlan.zhihu.com/p/61944055

 作者：李威威 来源：简书

链接：https://www.jianshu.com/p/2ea0406d0793

推荐阅读

数据预处理|关于标准化和归一化的一切

【干货收藏】人工智能必看的45篇论文

收藏 | 数据分析师最常用的10个机器学习算法！

7步搞定数据清洗－Python数据清洗指南

回归、分类与聚类：三大方向剖解机器学习算法的优缺点(附Python和R实现)