自动控制原理笔记-传递函数

目录

拉普拉斯反变换：

用拉普拉斯变换求解常微分方程的步骤：

部分分式展开法：

留数法：

零极点图:

传递函数

定义：

传递函数的标准形式：

传递函数的性质：

传递函数的局限性：

小结：

拉普拉斯反变换：

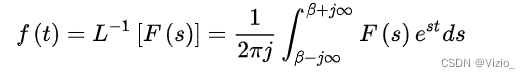
用拉普拉斯变换求解常微分方程的步骤：

1，等式两边进行拉普拉斯变换

2，将Y(s)分离出来

3，进行拉普拉斯反变换得到y(t)表达式

部分分式展开法：

将X（s）分解为因式，然后利用拉普拉斯变换公式来求它的逆变换

留数法：

确定部分分式中待定系数的留数方法_bj_zhb的博客-CSDN博客_留数法求待定系数

零极点图:

系统传递函数G(s)的特征可由其极点和零点在 s复数平面上的分布来完全决定。用D(s)代表G(s)的分母多项式，M(s)代表G(s)的分子多项式，则传递函数G(s)的极点规定为特征方程D(s)=0的根，传递函数G(s)的零点规定为方程M(s)=0的根。极点（零点）的值可以是实数和复数，而当它们为复数时必以共轭对的形式出现，所以它们在s复数平面上的分布必定是对称于实数轴（横轴）的。

传递函数

定义：

在零初始条件下，线性定常系统输出量拉氏变换与输入量拉氏变换的比

G（s）=Y（s）/U（s）

传递函数的标准形式：

首1：分子多项式和分母多项式最高次项的系数都为1（一般为n次项）

尾1：分子多项式和分母多项式最低次项的系数都为1（一般为常数项）

其中尾1标准式中，提出的常数项比值为该系统的增益

传递函数的性质：

1、传递函数是一种数学模型，与系统的微分方程相对应。
2、是系统本身的一种属性，与输入量的大小和性质无关。
3、只适用于线性定常系统。
4、传递函数是单变量系统描述，外部描述。
5、传递函数是在零初始条件下定义的，不能反映在非零初始条件下系统的运动情况。
6、一般为复变量 S 的有理分式，即 n ≧ m。且所有的系数均为实数。
7、如果传递函数已知，则可针对各种不同形式的输入量研究系统的输出或响应。
8、如果传递函数未知，则可通过引入已知输入量并研究系统输出量的实验方法，确定系统的传递函数。
9、传递函数与脉冲响应函数一一对应，脉冲响应函数是指系统在单位脉冲输入量作用下的输出。

传递函数的局限性：

1、原则上不反映非零初始条件时系统响应的全部信息

2、适合于描述单输入，单输出系统

3、只能用于描述线性定常系统

小结：

传递函数的标准形式

传递函数的性质

求系统的：传递函数，增益，特征根及其相应模态，零极点图，单位脉冲响应，微分方程

最后

以上就是糟糕日记本为你收集整理的自动控制原理笔记-传递函数的全部内容，希望文章能够帮你解决自动控制原理笔记-传递函数所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。