基于 MATLAB 的 PCM 编码解码实现

关于 PCM 的原理在此不过多解释，代码使用的是 A 律 13 折线法。

抽样信号

抽样信号的 MATLAB 代码如下：

clear;
clc;
T=0.0005;
t=-0.01:T:0.01;
fs=2000;
sdt=1/fs;
t1=-0.01:sdt:0.01;
xt=cos(2*pi*30*t)+sin(2*pi*120*t);
st=cos(2*pi*30*t1)+sin(2*pi*120*t1);
max = max(abs(st));

% 原始信号
figure;
subplot(2,1,1);plot(t,xt);title('原始信号');grid on;
subplot(2,1,2);stem(t1,st,'.');title('抽样信号');grid on;

绘制出来的图像如下图：

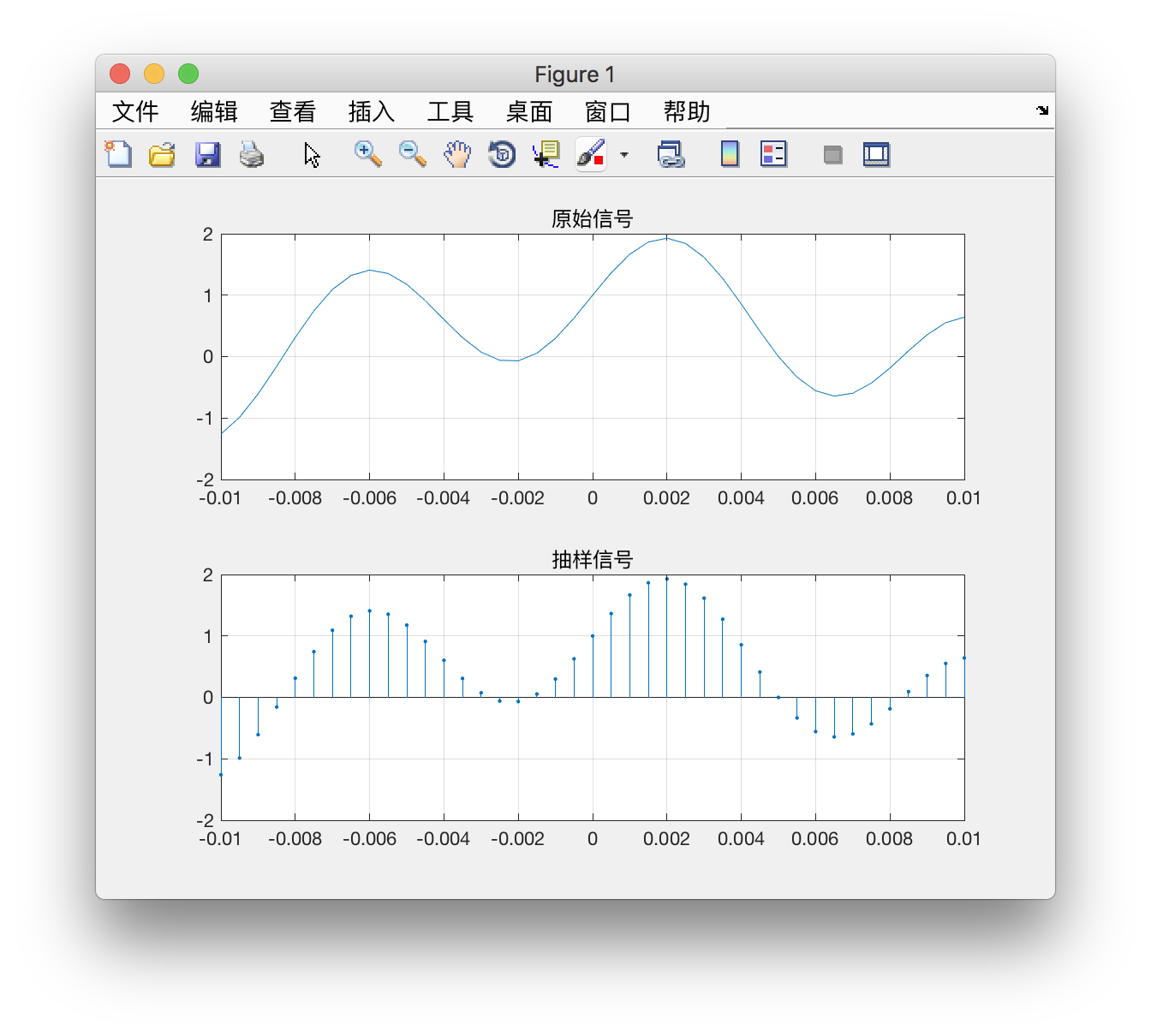
选择这个抽样频率是因为绘制出来的图像好看一点。可以看到上述代码中有一个 max 变量，这个后面要用到。

PCM 编码

分别得到符号位，段位码，段内码即可。代码如下：

function code=PCMcoding(S)
    z=sign(S);                                %判断S的正负
    MaxS=max(abs(S));                         %求S的最大值 
    S=abs(S/MaxS);                            %归一化
    Q=2048*S;                                 %量化
    code=zeros(length(S),8);                  %代码存储矩阵（全零）
    
    % 段落码判断程序
    for i=1:length(S)
        if (Q(i)>=128)&&(Q(i)<=2048)
            code(i,2)=1;            %在第五段与第八段之间，段位码第一位都为"1"
        end
        if (Q(i)>32)&&(Q(i)<128)||(Q(i)>=512)&&(Q(i)<=2048)
            code(i,3)=1;            %在第三四七八段内，段位码第二位为"1"
        end
        if (Q(i)>=16)&&(Q(i)<32)||(Q(i)>=64)&&(Q(i)<128)||(Q(i)>=256)&&(Q(i)<512)||(Q(i)>=1024)&&(Q(i)<=2048)
            code(i,4)=1;            %在二四六八段内，段位码第三位为"1"
        end
    end
    
    N=zeros(length(S));                              %段内码判断程序
    
    for i=1:length(S)
        N(i)=bin2dec(num2str(code(i,2:4)))+1;        %找到code位于第几段
    end
    
    a=[0,16,32,64,128,256,512,1024];                 %量化间隔
    b=[1,1,2,4,8,16,32,64];                          %除以16，得到每段的最小量化间隔
    for i=1:length(S)  
        q=ceil((Q(i)-a(N(i)))/b(N(i)));              %求出在段内的位置
        if q==0
            code(i,(5:8))=[0,0,0,0];                 %如果输入为零则输出"0"
        else k=num2str(dec2bin(q-1,4));              %编码段内码为二进制
            code(i,5)=str2num(k(1));
            code(i,6)=str2num(k(2));
            code(i,7)=str2num(k(3));
            code(i,8)=str2num(k(4));
        end
        if z(i)>0
            code(i,1)=1;
        elseif z(i)<0
            code(i,1)=0;
        end                                           %符号位的判断
    end
    code = reshape(code', 1, []);
end

将 PCM 编码抽象成了一个函数，这样方便在后来的过程中调用。注意到编码阶数后有一个重整矩阵维度的操作，这是因为刚编码完的数据是 a*8 的矩阵，为了后续操作方便要把它变成 1*8a 的矩阵。完成函数后绘图：

% PCM 编码
pcm_encode = PCMcoding(xt);

figure;
stairs(pcm_encode);
axis([0 20 -0.1 1.1]);
title('PCM 编码');
grid on;

这里选择 20 个码元来看看效果，因此将坐标设为 0 20 。绘出的图如下：

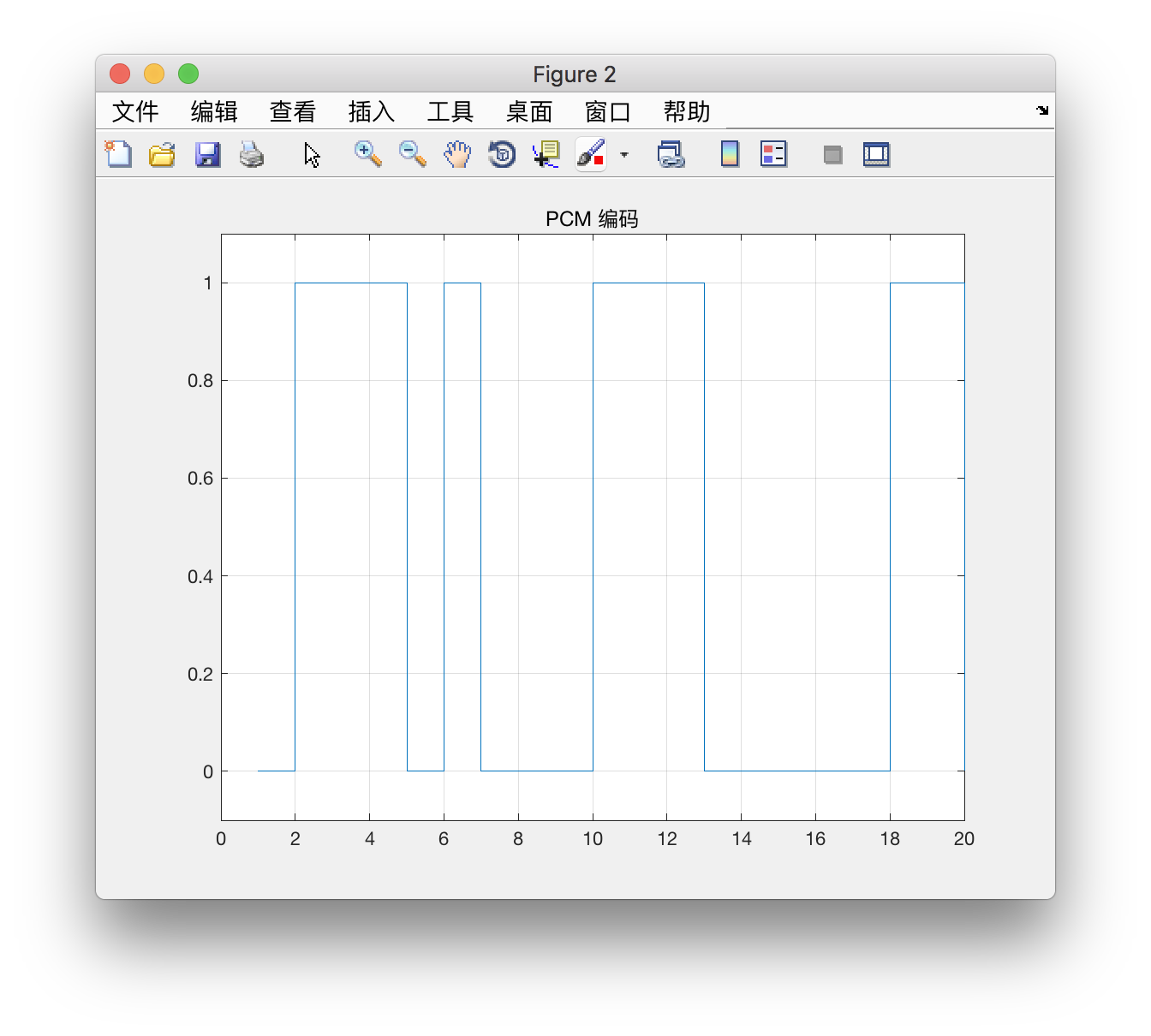
PCM 解码

注意到编码时有一个归一化的操作，因此信号幅度已经丢失，在解码时要将上述提到的 max 参数传入，以便解码恢复到原来的幅度。代码如下：

function s=PCMdecoding(encode, max)
    encode=(reshape(encode',8,length(encode)/8))';
    l=size(encode,1);
    a=[0,16,32,64,128,256,512,1024];
    b=[1 1 2 4 8 16 32 64];
    c=[0 1.5:15.5];
    for i=1:l
        x=encode(i,1);
        T=bin2dec(num2str(encode(i,(2:4))))+1;
        Y=bin2dec(num2str(encode(i,(5:8))));
        if Y==0
            k(i)=a(T)/2048;
        else
            k(i)=(a(T)+b(T)*c(Y))/2048;
        end
        if x==0
            s(i)=-k(i);
        else
            s(i)=k(i);
        end
    end
    s = s*max;
end

解码的时候有一个重塑矩阵形状的操作，同样为了解码方便。通常编码后还会使用信道编码等，因此编码时有一个重塑的操作，解码时又一个重塑操作。解码完成可视化一下：

% PCM 译码
pcm_decode = PCMdecoding(pcm_encode, max);

figure;
subplot(2,1,1);plot(t, pcm_decode);
title('PCM 译码');grid on;

subplot(2,1,2);plot(t,xt);
title('原始信号');grid on;

解码后的信号如下：

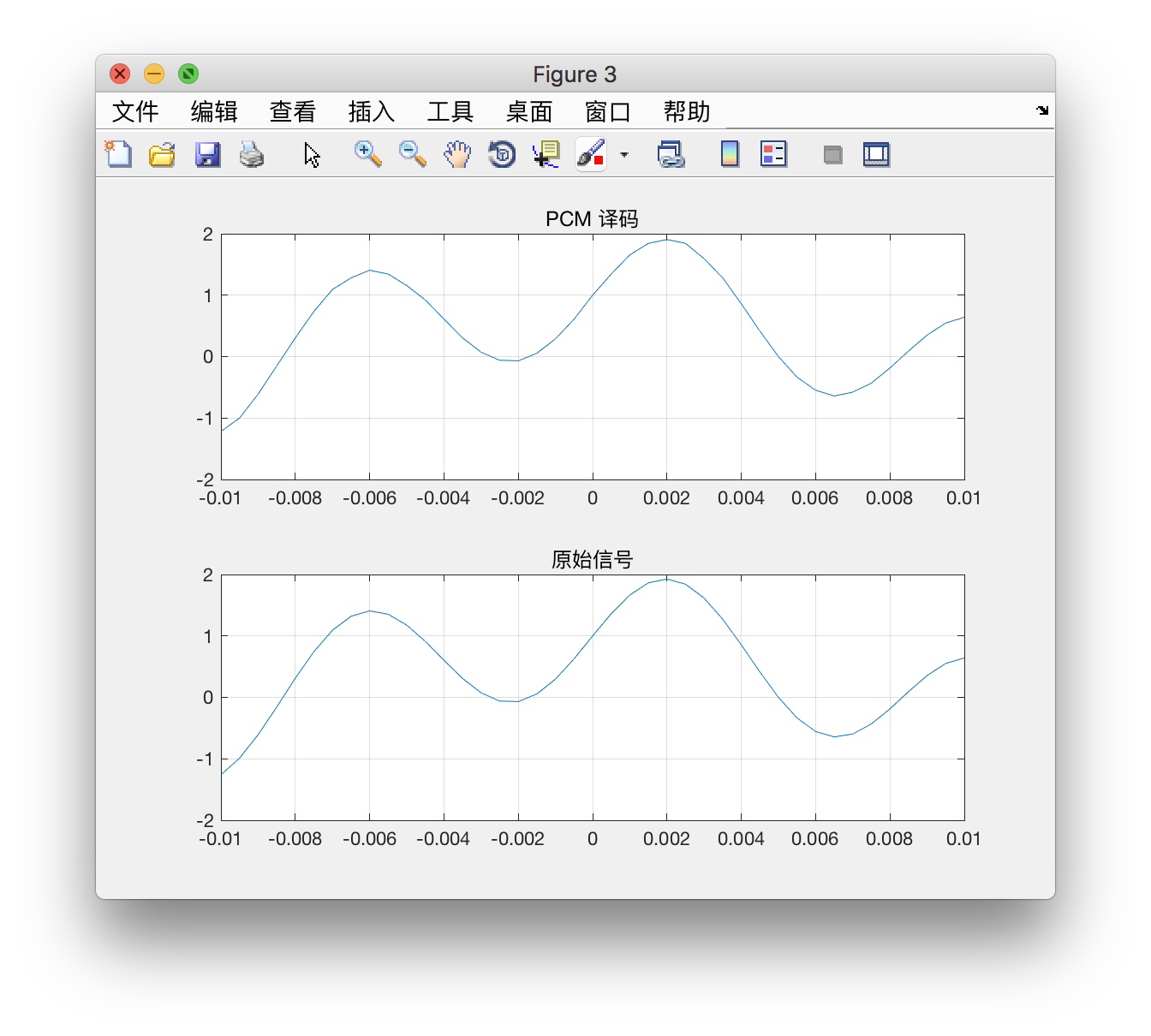
效果还行。

失真度分析

失真度分析代码如下：

% 计算失真度
da=0; 
for i=1:length(t)
    dc=(st(i)-pcm_decode(i))^2/length(t);
    da=da+dc;
end
fprintf('失真度是：%.6fn',da);

在此保留了六位小数，输出为 失真度是：0.000174 。

最后

以上就是缓慢鞋垫为你收集整理的基于 MATLAB 的 PCM 编码解码实现基于 MATLAB 的 PCM 编码解码实现的全部内容，希望文章能够帮你解决基于 MATLAB 的 PCM 编码解码实现基于 MATLAB 的 PCM 编码解码实现所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。